Fussy's Diary

蒸し暑い夜です。温度計を見たら現在 27 度。

今日は一冊の本を紹介します。

「確率・統計入門」 小針あき宏著 (岩波書店)
ISBN 978-4-00-005157-6

著者はこの本が出版される前、原稿をひと通り書き上げて間もなく亡くなり、有志によって原稿の見直しを行なって出版されたという特異な経歴を持った参考書です。それなりの前提知識は必要で、自分も理解するのには非常に時間がかかりました。今では 7 〜 8 割程度は理解できたのではないかと思っていますが、それまでには他の参考書も利用する必要があったので、全てがこの一冊で足りるというわけにはいかないものの、逆にこの本のおかげでレベルをかなり上げることができたと思っています。書き方も独特で、ところどころにユーモアを交えつつ、突然高度な話題を持ちだしたりして一筋縄ではいかないところもあります。こんな癖のある参考書は他にはないでしょうね。

もし書店なんかで見かけたら最初の章に少し目を通してみて、もし面白そうだと感じることができれば購入することをお勧めします。最近になって、「確率空間」ではなく「確率モデル」という言葉を使った意味が本当に理解できるようになった気がします。  

NHK の番組「ピタゴラスイッチ」は、古代ギリシャの数学者「ピタゴラス」が名前の由来になっていますが、番組の中の登場人物には「ピタ」「ゴラ」「スー」がいるということをついさっき知りました。

ピタゴラスの名前が付いた有名な定理「ピタゴラスの定理」は、直角三角形の斜辺の長さを c、その他の辺の長さを a, b としたときに

c² = a² + b²

が成り立つというもの。三平方の定理とも呼ばれ、確か小学校で習うのではなかったでしょうか。しかし、考え方を変えるとこの定理が

c = a + b

となってしまいます。

まず、最初に長方形からスタートして、四つの角のうちいずれかを長方形の形に 1 / 4 削ります。これで削った側には二つの角ができるので、次にこの角を長方形の形に 1 / 8 削ります。この操作を繰り返していきます。



操作を繰り返すと、その形は直角三角形にいくらでも近づきます。しかし、階段部分の長さはいくら削っても変化せず、斜辺以外の辺の和と等しいままです。この極限を考えると、斜辺の長さが他の二辺の和に等しい直角三角形ができあがります。斜辺に見える部分は実際には階段状態のままだから違うとも考えられますが、少なくとも面積はいくらでも近づけることができます。

少し前にこれを思い付き、矛盾点がどこかにないかを考えてみたのですが、今のところは解なしの状態です。フラクタル図形などと同じ考え方になるのでしょうかね。そもそも上のような図形は三角形とは呼べないですけどね。面積は限りなく等しい別の図形というとらえ方が正解なのかも。

ちなみに、ピタゴラスの定理の証明法はたくさんあります。その中の一つを紹介。



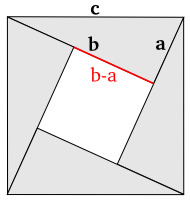
上図において、直角三角形の斜辺がちょうど大きな正方形の辺になるように配置されています。中央にできる小さな三角形は、直角三角形の二辺の差を一辺の長さとする正方形です。斜辺の長さを c、その他の辺の長さを a, b ( 但し b > a ) とすれば

大きな正方形の面積 = c²
四つの直角三角形の面積 = 4 x ab / 2 = 2ab
小さな正方形の面積 = ( b - a )²

なので、四つの直角三角形と小さな正方形の面積の和が大きな正方形の面積に等しくなることから

( b - a )² + 2ab = a² + b² = c²

でピタゴラスの定理が得られます。他にも証明法はたくさんあるので、Wikipedia を参考に (但し、英語版の方です)。  続きを読む

少し前に、D-Wave というカナダのベンチャー企業が実用的な量子コンピュータを発表したことが話題になっていました。

量子コンピュータ、ずっと未来の話かと思ってましたが、利用している原理が異なっていたり用途が限られているとはいえ実用的なものがすでに完成しているというのには驚きです。同じような「用途限定」の製品が他にも発表されたらと想像すると何だかワクワクしますね (ちなみに、世界中でさかんに研究されている、量子ゲートなるものを使った汎用的なコンピュータはまだまだ完成が先の話になるようです)。
量子力学には興味はあってもまだほとんど未知の分野で、いつか勉強してみたいとも思っています。しかし、物理学はあまりちゃんと勉強してこなかったので、高校で習う力学すらちゃんと理解しているかどうか怪しいです。以前、物理シミュレーションなんかを作ってみたいと思い立ち、何冊か古典力学の本なんかを買いました。量子力学の教科書なんかを入手しても、読むことなどできるでしょうか。いや、それでなくてもまだきちんと読んでいない参考書が何冊も残っているというのに...  

ノアの方舟を題材にした映画が公開予定です。

新聞にも宣伝があって、出演者を見たら結構豪華。役者の名前をそれほど知らない自分でもほとんど知っている人ばかりでした。ジェニファー・コネリーといえば「レオン」に出演した女の子だったっけ、スター・ウォーズにも出ていたよね... と考えた後、違うことに気づいて「ラビリンス」でデビッド・ボウイと共演した女優だと思い出し、じゃあ「レオン」に出演したのは誰だっけと思いだそうとしても名前が出てきませんでした。一日経って、ようやくナタリー・ポートマンの名前が浮かんで、いよいよボケが始まったのかと少々へこみました。いや、たまに名前が出てこないことがあるんですよ、本当に。

自分にとって、ジェニファー・コネリーといえば「ラビリンス」。少し前に DVD を購入しました。今でも楽しめる、非常に面白い映画です。超大作というわけではないですが、こういった映画はすごく好きです。「ウィロー」なんかもまた見たいですね。  

今日、テレビで喫茶「マウンテン」が紹介されてました。

他にはない奇抜なメニューで非常に有名な喫茶店ですが、20 年以上前からすでにその名は知られていて、近隣の学生(特に体育会系)に人気があったようです。小倉抹茶スパもその頃すでにあって、主に罰ゲームに利用されていたとか。食べた人からの話では小倉が口直しになるとのこと。麺のほうが小倉よりも甘いそうです。ちなみに、マウンテンで食事することを「山に登る」、完食出来たら「登頂」、途中で断念したら「遭難」といいます。それにしても、いつ頃から全国に知られるようになったんでしょうかね。自分はまだ食べたことはありません。
名古屋の名物として挙げられるものでいつも不思議に思うのが「エビフライ」と「みそカツ」で、少なくとも子供の頃は、「エビフライ」は名物などではなかったし「みそカツ」を食べた覚えもないです。これもいつ頃からそうなったのか、不思議です。

「数学問題 bot」で前から悩んでした問題がようやく解けました。解けないとなると意地になってしまい、昨日と今日はこの問題のことばかり考えていた気がします。

---

■ 自然数 n と m について、n² + m と n² - m がともに平方数であるなら、m は 24 で割り切れることを示せ (第24回シュプリンガー数学コンテスト)

n² + m = ( n + a )²
n² - m = ( n - b )²

とします。但し、b > 0, a > 0 とします。右辺を展開して整理すると、

n² + m = n² + 2na + a²
n² - m = n² - 2nb + b²

より

m = 2na + a²
m = 2nb - b²

なので、m について解くと

m = ab( a + b ) / ( b - a )

n について解くと

n = ( a² + b² ) / 2( b - a )
= [ ( b - a )² + 2ab ] / 2( b - a )
= ( b - a ) / 2 + ab / ( b - a )

となります。n の式から、a² + b² は偶数でなければ 2( b - a ) で割り切ることができないので、a, b はどちらも偶数または奇数となります。また、ab は b - a で割り切れる必要があり、a, b が両方とも奇数の場合、ab が奇数、b - a が偶数となるので、a, b はどちらも偶数である必要があります。そこで、a → 2a, b → 2b と置き換えて m, n を計算すると、

m = 2a・2b( 2a + 2b ) / ( 2b - 2a )
= 4ab( a + b ) / ( b - a )

n = ( 2b - 2a ) / 2 + 2a・2b / ( 2b - 2a )
= ( b - a ) + 2ab / ( b - a )

となります。n の式から、今度は 2ab が偶数であることから b - a も偶数である必要があるので b - a = 2c と置き換えると、

m = 4a( a + 2c )( 2a + 2c ) / 2c
= 4a( a + 2c )( a + c ) / c

n = 2c + 2a( a + 2c ) / 2c
= 2c + a( a + 2c ) / c

となります。n が整数となるためには、a/c, a/c + 2 のいずれかが整数となる必要があり、すなわち a が c で割り切れることになるので、a = kc として

m = 4kc( kc + 2c )( kc + c ) / c
= 4k( k + 1 )( k + 2 )c²

という結果が得られます。k, k + 1, k + 2 はいずれか一つが必ず 3 の倍数になり、少なくとも一つは偶数になるので、m は必ず 24 の倍数となります。

ところで、今までチャレンジした問題は数論が多いようです。特に選んでいるわけではないのですが、ほとんどパズルを解く感覚でやっているからでしょうか。今度は他のジャンルにも挑戦してみようと思います。  

最近、仕事が大変な状態でかなり疲れがたまっています。

「効率よく仕事しろ」 という言葉をよく聞きますが、個々人は効率よくこなしていこうとみんな努力してるんですよね。で、一番効率を悪くしているのが組織全体での決まりごと。とにかく誰が見ても明らかに効率が悪いのにそれが慣例化している。こういう企業は日本だけなんでしょうかね。

で、効率というキーワードでググってみたら、「仕事を効率良くこなすためのシンプルな 13 の習慣」というページを見つけました。古い記事ですが、役に立ちそうなことが列挙されています。すでに実践しているもの、何となくやっているものも含まれていますが、意識して仕事するようにするとまた違うかもしれませんね。もちろん、仕事だけではなくプライベートにも役に立ちそうです。

息抜きに「数学問題 bot」の問題を解いてみました。

---

■ 2 以上の自然数 n に対し、n と n² + 2 がともに素数になるのは n = 3 の場合に限ることを示せ。( 06 京都前期・理 )

n が 3 以外の素数の時、n² + 2 が合成数であることを証明すれば十分です。

n は 3 以外の素数なので、3 で割った時の余りは 1 か 2 のいずれかになります。従って、余りが 1 ならば n - 1 が、余りが 2 ならば n + 1 が 3 で割り切れます。従って、

n² + 2 = ( n + 1 )( n - 1 ) + 3

より n² + 2 は必ず 3 で割り切れることになり、n² + 2 は合成数です。

古典数論の問題は、実際に具体的な数値で試してみると解法が見つかることが多いです。この問題でも、n に素数を代入していくと

5² + 2 = 27
7² + 2 = 51
11² + 2 = 123

となって、全て 3 で割り切れることがわかります。

例によって、答えのチェックはしていないので合っているという保証はありません。  

ホームページの更新、次をどうするか少々悩んでいます。

アルゴリズムのコーナーの更新をするか、プログラムの作成に専念するか、決めかねている状態で、DTMの環境を整えたいというのもありますがこれは少し時間が必要になりそうなので、まあ長い目で見るとしてとりあえず保留とすれば、

・古いページの見直し(これは進行中)
・統計解析のテーマの更新(ポアソン解析あたりを考えています)
・曲線描画(NURBS)
・画像加工ソフト作成(今までのアルゴリズムの集大成)

あたりを目論んでます。特に要望があるわけではなく、できるものから順番に進めるつもりで、ソフト作成は今年の抱負なので今年中には完成させたいところ。まだ物理シミュレータだとかパターン認識なんかも勉強したいんですけど、とにかく時間の許す限りはがんばるつもりです。

＊宇宙飛行士の若田光一さんが地球に帰還された記事を見て、50 歳という年齢にビックリ。次に搭乗される予定の油井亀美也さんが 44 歳とあまり年齢が変わらないということで、ますますガンバらなければと感じてしまいます。それにしてもすごいパワーだと思います。  

今日は母の日です。

Amazon で便利そうなフードプロセッサを見つけ、プレゼントとして購入。今日、箱から取り出してみました。山芋や納豆のような粘性のあるものから、コーヒー、氷といった硬いものまで利用できるという優れもの。しかし、利用法はほんの少ししか書いていないので、レシピ本なんかもいっしょに買っておいた方がよかったかもしれません。まあ、喜んでもらえたので良しとしましょう。ちなみに購入したのは

山本電気 MICHIBA KITCHEN PRODUCT マスターカット Glossy Red MB-MM22R

という商品です。  

久しぶりにゲームを購入しました。




「トゥームレイダー」は前から買うつもりだったもの。「テラリア」は偶然見つけて面白そうだったのでいっしょに購入。「トゥームレイダー」の最初の方だけ少しプレイしました。昔のような謎解き主体のものではなく、戦闘の要素がかなり多くなっているような印象です。経験値の概念もあって、レビューなんかにもある通り、今までとは異なるものと考えたほうがよさそうです。しかし、今のところは結構楽しくプレイしてます。ちなみに様子見のためイージーでプレイ。それにしても、相変わらず始めるのが非常に遅いです。

PS4 が発売されて結構経ちますが、今のところは購入予定はなく、少なくとも 1 ～ 2 年は PS3 のままのつもりです。PS3 はゲーム機というよりは DVD 再生 + テレビ録画機の用途の割合の方が高く、ゲームが発売されなくなったとしてもほとんど問題にならないので、よほど面白そうなゲームが PS4 で発売されない限りは買い替えはなさそうです。ゲームをするなら、Wii なんかの方が興味があるんですけどね。  

連休明けの出勤三日間がようやく終わり、ほっと一息ついたところです。

最近は本を読む頻度が少なくなってしたような気がします。まだ未読の本が何冊かあって、いつか読もうと思いつつもそのまま放置。で、また新たに本が欲しくなるという悪循環です。連休中も結局、本はあまり読みませんでした。
昔、推理小説が好きで何冊も読んでいた時期があります。エラリー・クイーンやアガサ・クリスティーといった定番はもちろん、少しマイナーなところではヴァン・ダインやディクスン・カーも何冊か読んでます。ここで個人的にお勧めの小説を紹介します(結構、有名なものばかりかな？)

■ Yの悲劇 (エラリー・クイーン)

エラリー・クイーンの初期の作品(国名シリーズ)は謎解きを楽しむことを主眼に作られたものが多く、個人的にはそれほど好きなものはありません(あまり印象にも残ってないです)。唯一「エジプト十字架の謎」が結構面白かった気がします。エラリー・クイーンの作品で一番のお気に入りは「Xの悲劇」から始まる四部作で、特に「Yの悲劇」は作品の持つ雰囲気が好きで、最後の真相がわかった時のインパクトもかなり強烈でした。

■ そして誰もいなくなった (アガサ・クリスティ)

これも謎解きよりは作品の持つ独特の雰囲気が好きでした。最後にわかる真相も驚きでしたけどね。アガサ・クリスティは他にも「アクロイド殺し」「オリエント急行殺人事件」「ナイルに死す」等々、いい作品がたくさんあります。

■ グリーン家殺人事件 (ヴァン・ダイン)

「Yの悲劇」は、この「グリーン家殺人事件」の影響を強く受けたと言われていますが、確かに読んでみるとよくわかります。ちなみに、読んだのはこちらの「グリーン家殺人事件」が先でした。ヴァン・ダインの作品も有名どころはだいたい読んでます。

■ 三つの棺 (ディクスン・カー)

確か、ディクスン・カーの中で最初に読んだ作品です。プロットは結構複雑ですが、内容としては面白く一気に読みました。ディクスン・カーの作品で他に印象深かったのは短編集の「妖魔の森の家」でしょうか。今気づいたのですが、「皇帝のかぎ煙草入れ」をまだ読んでしませんでした...

■ 獄門島 (横溝正史)

テレビなどでも何回か放映されていたので非常に有名な作品ですね。横溝正史の小説としては、これと「悪魔が来りて笛を吹く」くらいしか読んだことがなくて、他の作品はテレビで見たものばかりです。「犬神家の一族」は大好きな作品でした。

こうやって並べてみると、少しオカルトっぽい作品が多いような気もしますね。  

久々の仕事は疲れます。明日はかなりハードな一日になりそうです。

レツゴー三匹のじゅんさんが亡くなったそうです。享年 68 歳。ご冥福をお祈りします。レツゴー三匹の漫才を見たのはかなり昔のことだったので、どんなものだったか覚えていません。それよりも、太平サブロー・シローとラサール石井によるモノマネの方がインパクトがありすぎて記憶に残っています。最初のつかみの部分も、やはりモノマネの方しか思い浮かばない始末。
トリオというと他にチャンバラトリオというのもありました。他にもかしまし娘とか。子供の頃、正月になるとこういった芸人たちがテレビに出演したりして、それを見るのがすごく楽しかったのを記憶しています。そういった方たちがいなくなってゆくのは寂しい気がします。  

明日で休日が終わり、またしばらくは忙しい毎日が始まります。

昨日・今日はのんびりと過ごしていました。ぼんやりと次のテーマも考えていて、そのための本を読んだりもしていましたが、いつの間にか睡魔におそわれて眠ってしまい大して進んでいません。まあ、今まで通りあせらずにゆっくりとやっていくつもりです。

夕方頃から、「数学問題 bot」にチャレンジしていました。二問のうち片方は解けたので、解法を紹介してみたいと思います。これもあっているという保証はないです。

---

■ 2ⁿ + n² が素数であるような 2 以上の整数 n について、n を 6 で割った時の余りが 3 であることを示せ(第24回シュプリンガー数学コンテスト)

このまま眺めていても取り付く島もない状態なので、とりあえず小さな数からチェックしてみます。

n = 3 のとき 2³ + 3² = 8 + 9 = 17 で素数。
n = 4 のとき 2⁴ + 4² = 16 + 16 = 32
n = 5 のとき 2⁵ + 5² = 32 + 25 = 57
n = 6 のとき 2⁶ + 6² = 64 + 36 = 100
n = 7 のとき 2⁷ + 7² = 128 + 49 = 177
n = 8 のとき 2⁸ + 8² = 256 + 64 = 320
n = 9 のとき 2⁹ + 9² = 512 + 81 = 593 で素数。

明らかに、n が偶数なら 2ⁿ + n² も偶数なので除外できます。n = 5, 7 のとき結果は 3 の倍数なので、n = 6k ± 1 ( k > 0 ) としたときにこれが 3 の倍数となるのではと推測してみます。そこで、この値を 2ⁿ + n² に代入して変形してみると、

2^6k±1 + ( 6k ± 1 )² = 36k² ± 12k + ( 2^6k±1 + 1 )

となります。もし任意の k に対して、2^6k±1 + 1 が 3 で割り切れれば、つまり 2^6k±1 を 3 で割った余りが 2 なら、2ⁿ + n² は 3 で割り切れることになって必ず合成数となります。k = 1 のとき、

2^6k-1 = 2⁵ = 32
2^6k+1 = 2⁷ = 128

なので、どちらも 3 で割ると 2 余ります。3m + 2 で表される ( 3 で割って 2 余る) 数に 2⁶ = 64 を掛けると

( 3m + 2 ) x 64 = 3 x 64m + 128 = 3 x ( 64m + 42 ) + 2 より やはり 2 余る数になるので、2^6k±1 は任意の k に対して必ず 2 余ることになり、n = 6k ± 1 の場合は必ず 3 の倍数なので素数にはならないことが示されました。よって、2ⁿ + n² が素数になるなら、それは必ず n = 6k + 3 で表されることになります。

逆は成り立つのでしょうか。

n = 15 のとき 2¹⁵ + 15² = 32768 + 225 = 32993 で素数。
n = 21 のとき 2²¹ + 21² = 2097152 + 441 = 2097593 で素数。
n = 27 のとき 2²⁷ + 27² = 134217728 + 729 = 134218457 で素数ではない(73 x 521 x 3529 )。

となるので、必ず成り立つというわけではありません。

ところで、下の問題も同時に考えていました。こちらの方が簡単だと思っていたのに、まだ解けていません。解法が見つかったらまた紹介しようかと思います。

■ 自然数 n と m について、n² + m とn² - m がともに平方数であるなら、m は 24 で割り切れることを示せ (第24回シュプリンガー数学コンテスト)
  

連休もあとわずかとなりました。

Daily Portal Z で 「オオグソクムシはカニとかシャコに近い味」という記事を発見。あの巨大なダンゴムシの親分を食べるの ? と思ったら、それは「ダイオウグソクムシ」で、「オオグソクムシ」は日本で獲れるもっと小さな種でした (ちなみに「ダイオウグソクムシ」は鳥羽水族館で実際に見ることができます)。

とは言ってもダンゴムシの親分に変わりはなく (実際、ダンゴムシやフナムシの仲間だそうです)、まさか食べられるとは思いませんでした。確かにダンゴムシも食用になると聞いたことはありますけどね。で、味はカニによく似ているとのことですが、残念ながら身の部分は非常に少なくたくさんは食べられなかったようです。

オオグソクムシ、写真を見るとなかなかかわいい顔をしています。しかし、裏返すとゴ○ブリに形が似ているというのが残念。ダイオウグソクムシの人気が結構高い気がするので、これを機会にオオグソクムシにももっと注目してほしいところ。

久々に「数学問題 bot」に挑戦。本当は他の問題にもチャレンジしていたのですが、解けたのはこれだけ (例によって答え合わせをしていないので合っている保証はありません)。

---

■ 1 から 5 までの自然数を 1 列に並べる。どの並べ方も同様の確からしさで発生する。このとき 1 番目と 2 番目と 3 番目の数の和と、3 番目と 4 番目と 5 番目の数の和が等しくなる確率を求めよ。ただし、各並べ方において、それぞれの数字は重複なく１度ずつ用いるものとする (10京都・理甲)

「1 番目と 2 番目と 3 番目の数の和と、3 番目と 4 番目と 5 番目の数の和が等しくなる」ということは、「1 番目と 2 番目の数の和と、4 番目と 5 番目の数の和が等しくなる」ことと同じなので、3 番目の数は無視できます。また、1 から 5 までの自然数の和は 15 で、1, 2, 4, 5 番目の数の和は 15 から 3 番目の数を引いた値になります。その結果は偶数でないと半分に分けることができないので、3 番目の数は必ず奇数の 1, 3, 5 となります。

ここから、i 番目の数を a[i] で表します。仮に、a[3] = 1 ならば、a[1] + a[2] = a[4] + a[5] = 7 になります。2 から 5 までの数でこの条件を満たす組み合わせは ( 2, 5 ) と ( 3, 4 ) のペアだけです。それぞれは ( a[1], a[2] ) と ( a[4], a[5] ) の間で交換が可能で、さらにその内部でも交換が可能なので、並べ方は 2 x 2 x 2 = 8 通りになります。a[1] から a[5] までを実際に並べてみると

( 2 5 1 3 4 ) ( 5 2 1 3 4 ) ( 2 5 1 4 3 ) ( 5 2 1 4 3 )
( 3 4 1 2 5 ) ( 4 3 1 2 5 ) ( 3 4 1 5 2 ) ( 4 3 1 5 2 )

です。a[3] = 3 ならば、組み合わせは ( 1, 5 ) と ( 2, 4 ) のペア、a[3] = 5 ならば、組み合わせは ( 1, 4 ) と ( 2, 3 ) のペアのみなので、やはりそれぞれ 8 通りです。よって、条件を満たす組み合わせは 8 x 3 = 24 通りとなります。最後に、全ての並べ方は 5! = 120 通りなので、確率は

24 / 120 = 1 / 5

となります。  

ようやく更新しました「アルゴリズムのコーナー」。今回は「順序ロジスティック回帰」がテーマです。

連休前はまだ具体的な計算方法がわからない状態で、連休開始から集中して解いていました。結局 3 日くらいを費やしてやっと計算結果の正しいプログラムが完成し、先ほど更新したところです。いろんなサイトを調べてみましたが、結局最後は自力で計算式を導いています。なので、他にもっとスマートなやり方があると思いますが、もし発見したらまた紹介するつもりです。

次のテーマの候補はいくつかあるものの、先に内容を理解してから進めたいので更新はしばらく先になるかもしれません。この間購入した「初音ミク」も少し歌わせてみただけで使っていないので、簡単な曲でも作ってみたいし。それよりも連休中はずっと家での作業だったので、少し外出したいです。散歩でもしないと体がなまってしまう...

今回更新した「順序ロジスティック回帰」へのリンク先は
http://fussy.web.fc2.com/algo/stat20_olr.htm
です。  

Twitter でおもしろいツイートを見つけました。

Zeno’s Paradox: Understanding Convergent & Divergent Series http://t.co/9DnkuNG2HP

— LiveScience (@LiveScience) 2014, 5月 1

「ゼノンのパラドックス」は「アキレスとカメ」の話が特に有名です。前方にいるカメをアキレスが追いかけるとします。その間の距離が 100m 離れていて、アキレスの方がカメよりも 10 倍速ければ、最初にカメのいた地点にアキレスが到達した時カメは 10m 先にいます。さらに追いかけてその地点に到達した時、カメは 1m 先にいます。これを繰り返していくと、10cm、1cm、1mm と距離は 1 / 10 ずつ短くなるものの、いつまで経っても間の距離はゼロになりません。つまり、永遠に追い越すことができないというのが、ギリシャ時代のの哲学者ゼノンの主張したパラドックスです。初めてこれを知ったのは確か小学生の頃で、当時は不思議に感じた記憶があります。

数学的には、有限な数を無限に続く和の形で表すことができることを意味します。例えば、

1 = 1 / 2 + 1 / 4 + 1 / 8 + 1 / 16 + ... + 1 / 2ⁿ + ...

というような式が挙げられます。ようかんなんかを半分に切る操作を無限に繰り返す様子をイメージすれば納得できるかと思います。
似たような話として、例えば 1 を 3 で割ると、

1 / 3 = 0.333333 ...

と 3 が無限に続きます。これに 3 を掛けると

0.333333 ... x 3 = 0.999999 ...

です。しかし、これは 1 / 3 x 3 を計算していることでもあるので答えは 1 にもなります。従って、

0.999999 ... = 1

という結論になります。このあたりを考えだすと頭が痛くなってくるので、この辺でやめておきます。  

現在、サンプル・プログラムの見直し中です。なかなかうまくいかず、今日一日苦しんでます。

計算結果がおかしく、その原因がどこにあるのかがまだわからない状態です。考えられる要因は、

・コーディングのミス
・コーディングは問題ないが、導き出した式のどこかに誤りがある
・そもそも、考え方に誤りがある

のいずれかです。つまり、全てにおいて誤っている可能性があるということです。なので、最初から見直しを進めている最中。しかし、さすがにもうかなり疲れてきたので、そろそろ今日は終わりにしようかと思います。

明日も一日がんばってみるつもりですが、さすがに連休中は外出もしたいところ。すこしは体を休めておきたいと思います。それにしても、もう五月ですね。今年も 1 / 3 が終わったということですか...

どこかにいい書籍はないものだろうか。