2014年05月25日
確率モデル
蒸し暑い夜です。温度計を見たら現在 27 度。
今日は一冊の本を紹介します。
「確率・統計入門」 小針あき宏著 (岩波書店)
ISBN 978-4-00-005157-6
著者はこの本が出版される前、原稿をひと通り書き上げて間もなく亡くなり、有志によって原稿の見直しを行なって出版されたという特異な経歴を持った参考書です。それなりの前提知識は必要で、自分も理解するのには非常に時間がかかりました。今では 7 〜 8 割程度は理解できたのではないかと思っていますが、それまでには他の参考書も利用する必要があったので、全てがこの一冊で足りるというわけにはいかないものの、逆にこの本のおかげでレベルをかなり上げることができたと思っています。書き方も独特で、ところどころにユーモアを交えつつ、突然高度な話題を持ちだしたりして一筋縄ではいかないところもあります。こんな癖のある参考書は他にはないでしょうね。
もし書店なんかで見かけたら最初の章に少し目を通してみて、もし面白そうだと感じることができれば購入することをお勧めします。最近になって、「確率空間」ではなく「確率モデル」という言葉を使った意味が本当に理解できるようになった気がします。
今日は一冊の本を紹介します。
「確率・統計入門」 小針あき宏著 (岩波書店)
ISBN 978-4-00-005157-6
著者はこの本が出版される前、原稿をひと通り書き上げて間もなく亡くなり、有志によって原稿の見直しを行なって出版されたという特異な経歴を持った参考書です。それなりの前提知識は必要で、自分も理解するのには非常に時間がかかりました。今では 7 〜 8 割程度は理解できたのではないかと思っていますが、それまでには他の参考書も利用する必要があったので、全てがこの一冊で足りるというわけにはいかないものの、逆にこの本のおかげでレベルをかなり上げることができたと思っています。書き方も独特で、ところどころにユーモアを交えつつ、突然高度な話題を持ちだしたりして一筋縄ではいかないところもあります。こんな癖のある参考書は他にはないでしょうね。
もし書店なんかで見かけたら最初の章に少し目を通してみて、もし面白そうだと感じることができれば購入することをお勧めします。最近になって、「確率空間」ではなく「確率モデル」という言葉を使った意味が本当に理解できるようになった気がします。
2014年05月25日
ピタゴラスの定理
NHK の番組「ピタゴラスイッチ」は、古代ギリシャの数学者「ピタゴラス」が名前の由来になっていますが、番組の中の登場人物には「ピタ」「ゴラ」「スー」がいるということをついさっき知りました。
ピタゴラスの名前が付いた有名な定理「ピタゴラスの定理」は、直角三角形の斜辺の長さを c、その他の辺の長さを a, b としたときに
c2 = a2 + b2
が成り立つというもの。三平方の定理とも呼ばれ、確か小学校で習うのではなかったでしょうか。しかし、考え方を変えるとこの定理が
c = a + b
となってしまいます。
まず、最初に長方形からスタートして、四つの角のうちいずれかを長方形の形に 1 / 4 削ります。これで削った側には二つの角ができるので、次にこの角を長方形の形に 1 / 8 削ります。この操作を繰り返していきます。

操作を繰り返すと、その形は直角三角形にいくらでも近づきます。しかし、階段部分の長さはいくら削っても変化せず、斜辺以外の辺の和と等しいままです。この極限を考えると、斜辺の長さが他の二辺の和に等しい直角三角形ができあがります。斜辺に見える部分は実際には階段状態のままだから違うとも考えられますが、少なくとも面積はいくらでも近づけることができます。
少し前にこれを思い付き、矛盾点がどこかにないかを考えてみたのですが、今のところは解なしの状態です。フラクタル図形などと同じ考え方になるのでしょうかね。そもそも上のような図形は三角形とは呼べないですけどね。面積は限りなく等しい別の図形というとらえ方が正解なのかも。
ちなみに、ピタゴラスの定理の証明法はたくさんあります。その中の一つを紹介。
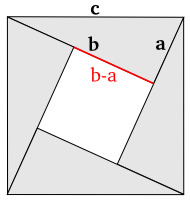
上図において、直角三角形の斜辺がちょうど大きな正方形の辺になるように配置されています。中央にできる小さな三角形は、直角三角形の二辺の差を一辺の長さとする正方形です。斜辺の長さを c、その他の辺の長さを a, b ( 但し b > a ) とすれば
大きな正方形の面積 = c2
四つの直角三角形の面積 = 4 x ab / 2 = 2ab
小さな正方形の面積 = ( b - a )2
なので、四つの直角三角形と小さな正方形の面積の和が大きな正方形の面積に等しくなることから
( b - a )2 + 2ab = a2 + b2 = c2
でピタゴラスの定理が得られます。他にも証明法はたくさんあるので、Wikipedia を参考に (但し、英語版の方です)。 続きを読む
ピタゴラスの名前が付いた有名な定理「ピタゴラスの定理」は、直角三角形の斜辺の長さを c、その他の辺の長さを a, b としたときに
c2 = a2 + b2
が成り立つというもの。三平方の定理とも呼ばれ、確か小学校で習うのではなかったでしょうか。しかし、考え方を変えるとこの定理が
c = a + b
となってしまいます。
まず、最初に長方形からスタートして、四つの角のうちいずれかを長方形の形に 1 / 4 削ります。これで削った側には二つの角ができるので、次にこの角を長方形の形に 1 / 8 削ります。この操作を繰り返していきます。

操作を繰り返すと、その形は直角三角形にいくらでも近づきます。しかし、階段部分の長さはいくら削っても変化せず、斜辺以外の辺の和と等しいままです。この極限を考えると、斜辺の長さが他の二辺の和に等しい直角三角形ができあがります。斜辺に見える部分は実際には階段状態のままだから違うとも考えられますが、少なくとも面積はいくらでも近づけることができます。
少し前にこれを思い付き、矛盾点がどこかにないかを考えてみたのですが、今のところは解なしの状態です。フラクタル図形などと同じ考え方になるのでしょうかね。そもそも上のような図形は三角形とは呼べないですけどね。面積は限りなく等しい別の図形というとらえ方が正解なのかも。
ちなみに、ピタゴラスの定理の証明法はたくさんあります。その中の一つを紹介。

上図において、直角三角形の斜辺がちょうど大きな正方形の辺になるように配置されています。中央にできる小さな三角形は、直角三角形の二辺の差を一辺の長さとする正方形です。斜辺の長さを c、その他の辺の長さを a, b ( 但し b > a ) とすれば
大きな正方形の面積 = c2
四つの直角三角形の面積 = 4 x ab / 2 = 2ab
小さな正方形の面積 = ( b - a )2
なので、四つの直角三角形と小さな正方形の面積の和が大きな正方形の面積に等しくなることから
( b - a )2 + 2ab = a2 + b2 = c2
でピタゴラスの定理が得られます。他にも証明法はたくさんあるので、Wikipedia を参考に (但し、英語版の方です)。 続きを読む





