2017年03月26日
放送大学
大相撲春場所はなんと稀勢の里が逆転優勝しました。怪我したときは今場所はダメかと思ってましたが、やはり横綱、すごいものです。
最近、BS 放送が見られるようになったので、どんなのが見られるのか番組表で調べてみたら、その中に放送大学がありました。量子力学の講義がありましたが、途中から見たらチンプンカンプンでした。他にもデジタル画像の処理や認識といった講義があり、こちらは内容もそれほど難しくないのでなかなかいいですね。しかし、概要の説明だけにとどまっているので、詳細な部分は自分で調べる必要があります。もしかしたら、講義用の本に詳しい解説があるのかもしれません。
調べてみると、一教科からでも受けられるみたいですね。時間があれば受講してみたいものです。
最近、BS 放送が見られるようになったので、どんなのが見られるのか番組表で調べてみたら、その中に放送大学がありました。量子力学の講義がありましたが、途中から見たらチンプンカンプンでした。他にもデジタル画像の処理や認識といった講義があり、こちらは内容もそれほど難しくないのでなかなかいいですね。しかし、概要の説明だけにとどまっているので、詳細な部分は自分で調べる必要があります。もしかしたら、講義用の本に詳しい解説があるのかもしれません。
調べてみると、一教科からでも受けられるみたいですね。時間があれば受講してみたいものです。
2017年03月19日
名大入試問題 2017 (6)
明日は「春分の日」です。個人的にはもっと暖かくなってほしいところです。
2017 年名大入試問題のラストです。結構、悩まされました。
-----
次の問に答えよ。
(1) 次の条件 (*) を満たす 3 つの自然数の組 ( a, b, c ) をすべて求めよ。
(*) a < b < c かつ 1/a +1/b + 1/c = 1/2 である。
(2) 偶数 2n ( n ≥ 1 ) の 3 つの正の約数 p, q, r で p > q > r と p + q + r = n を満たす組 ( p, q, r ) の個数を f(n) とする。ただし、条件を満たす組が存在しない場合は、f(n) = 0 とする。n が自然数全体を動くときの f(n) の最大値 M を求めよ。また、f(n) = M となる自然数 n の中で最小のものを求めよ。
(1) (*) より 1/a > 1/2 なので a > 2 になります。
a = 3 のとき、1/b + 1/c = 1/2 - 1/3 = 1/6 より 1/b < 1/6 なので b > 6 です。
b = 7 のとき 1/c = 1/6 - 1/7 = 1/42、b = 8 のとき 1/c = 1/6 - 1/8 = 1/24、b = 9 のとき 1/c = 1/6 - 1/9 = 1/18、b = 10 のとき 1/c = 1/6 - 1/10 = 1/15、b = 11 のとき 1/c = 1/6 - 1/11 = 5/66、b = 12 のとき 1/c = 1/6 - 1/12 = 1/12 で b = c となるのでこれ以上はありません。よって、( 3, 7, 42 ), ( 3, 8, 24 ), ( 3, 9, 18 ), ( 3, 10, 15 ) が得られます。
a = 4 のとき、1/b + 1/c = 1/2 - 1/4 = 1/4 より 1/b < 1/4 なので b > 4 です。
b = 5 のとき 1/c = 1/4 - 1/5 = 1/20、b = 6 のとき 1/c = 1/4 - 1/6 = 1/12、b = 7 のとき 1/c = 1/4 - 1/7 = 3/28、b = 8 のとき 1/c = 1/4 - 1/8 = 1/8 で b = c となるのでこれ以上はありません。よって、( 4, 5, 20 ), ( 4, 6, 12 ) が得られます。
a = 5 のとき、1/b + 1/c = 1/2 - 1/5 = 3/10 より 1/b < 3/10 なので b > 3 ですが、a = 5 なので b ≥ 6 となります。
b = 6 のとき 1/c = 3/10 - 1/6 = 2/15、b = 7 のとき 1/c = 3/10 - 1/7 = 11/70 > 1/7 で b > c となるのでこれ以上はありません。
a = 6 のとき、1/b + 1/c = 1/2 - 1/6 = 1/3 より 1/b < 1/3 なので b > 3 ですが、a = 6 なので b ≥ 7 となります。
b = 7 のとき 1/c = 1/3 - 1/7 = 4/21 > 1/7 で b > c となるのでこれ以上はありません。
以下、a ≥ 6 のときは b ≥ a + 1 であり、1/c = 1/2 - 1/a - 1/(a+1) ≥ 1/2 - 1/6 - 1/7 = 4/21 > 1/7 より c < 7 となり、 a < b < c を満たさなくなるのでこれ以上はありません。
よって、( 3, 7, 42 ), ( 3, 8, 24 ), ( 3, 9, 18 ), ( 3, 10, 15 ), ( 4, 5, 20 ), ( 4, 6, 12 ) の 6 つになります。
(2) p = 2n/p'、q = 2n/q'、r = 2n/q' とすると、p' < q' < r' かつ 1/p' + 1/q' + 1/r' = p/2n + q/2n + r/2n = 1/2 となるので、( p', q', r' ) の組は (1) でもとめたものに限ります。以下、k を 1 以上の整数とします。
( p', q', r' ) = ( 3, 7, 42 ) のとき、n = 21k ならば p = 14k, q = 6k, r = k で p + q + r = 21k なので成り立ちます。
( p', q', r' ) = ( 3, 8, 24 ) のとき、n = 12k ならば p = 8k, q = 3k, r = k で p + q + r = 12k なので成り立ちます。
( p', q', r' ) = ( 3, 9, 18 ) のとき、n = 9k ならば p = 6k, q = 2k, r = k で p + q + r = 9k なので成り立ちます。
( p', q', r' ) = ( 3, 10, 15 ) のとき、n = 15k ならば p = 10k, q = 3k, r = 2k で p + q + r = 15k なので成り立ちます。
( p', q', r' ) = ( 4, 5, 20 ) のとき、n = 10k ならば p = 5k, q = 4k, r = k で p + q + r = 10k なので成り立ちます。
( p', q', r' ) = ( 4, 6, 12 ) のとき、n = 6k ならば p = 3k, q = 2k, r = k で p + q + r = 6k なので成り立ちます。
すなわち、n = 6k, 9k, 10k, 12k, 15k, 21k のとき p + q + r = n を満たす ( p, q, r ) の組が存在することになります。これらの最初公倍数は 2・2・3・3・5・7k = 1260k で、このとき f(n) = 6 となります。よって、M = 6 で、最小の数は 1260 です。
2017 年名大入試問題のラストです。結構、悩まされました。
-----
次の問に答えよ。
(1) 次の条件 (*) を満たす 3 つの自然数の組 ( a, b, c ) をすべて求めよ。
(*) a < b < c かつ 1/a +1/b + 1/c = 1/2 である。
(2) 偶数 2n ( n ≥ 1 ) の 3 つの正の約数 p, q, r で p > q > r と p + q + r = n を満たす組 ( p, q, r ) の個数を f(n) とする。ただし、条件を満たす組が存在しない場合は、f(n) = 0 とする。n が自然数全体を動くときの f(n) の最大値 M を求めよ。また、f(n) = M となる自然数 n の中で最小のものを求めよ。
(1) (*) より 1/a > 1/2 なので a > 2 になります。
a = 3 のとき、1/b + 1/c = 1/2 - 1/3 = 1/6 より 1/b < 1/6 なので b > 6 です。
b = 7 のとき 1/c = 1/6 - 1/7 = 1/42、b = 8 のとき 1/c = 1/6 - 1/8 = 1/24、b = 9 のとき 1/c = 1/6 - 1/9 = 1/18、b = 10 のとき 1/c = 1/6 - 1/10 = 1/15、b = 11 のとき 1/c = 1/6 - 1/11 = 5/66、b = 12 のとき 1/c = 1/6 - 1/12 = 1/12 で b = c となるのでこれ以上はありません。よって、( 3, 7, 42 ), ( 3, 8, 24 ), ( 3, 9, 18 ), ( 3, 10, 15 ) が得られます。
a = 4 のとき、1/b + 1/c = 1/2 - 1/4 = 1/4 より 1/b < 1/4 なので b > 4 です。
b = 5 のとき 1/c = 1/4 - 1/5 = 1/20、b = 6 のとき 1/c = 1/4 - 1/6 = 1/12、b = 7 のとき 1/c = 1/4 - 1/7 = 3/28、b = 8 のとき 1/c = 1/4 - 1/8 = 1/8 で b = c となるのでこれ以上はありません。よって、( 4, 5, 20 ), ( 4, 6, 12 ) が得られます。
a = 5 のとき、1/b + 1/c = 1/2 - 1/5 = 3/10 より 1/b < 3/10 なので b > 3 ですが、a = 5 なので b ≥ 6 となります。
b = 6 のとき 1/c = 3/10 - 1/6 = 2/15、b = 7 のとき 1/c = 3/10 - 1/7 = 11/70 > 1/7 で b > c となるのでこれ以上はありません。
a = 6 のとき、1/b + 1/c = 1/2 - 1/6 = 1/3 より 1/b < 1/3 なので b > 3 ですが、a = 6 なので b ≥ 7 となります。
b = 7 のとき 1/c = 1/3 - 1/7 = 4/21 > 1/7 で b > c となるのでこれ以上はありません。
以下、a ≥ 6 のときは b ≥ a + 1 であり、1/c = 1/2 - 1/a - 1/(a+1) ≥ 1/2 - 1/6 - 1/7 = 4/21 > 1/7 より c < 7 となり、 a < b < c を満たさなくなるのでこれ以上はありません。
よって、( 3, 7, 42 ), ( 3, 8, 24 ), ( 3, 9, 18 ), ( 3, 10, 15 ), ( 4, 5, 20 ), ( 4, 6, 12 ) の 6 つになります。
(2) p = 2n/p'、q = 2n/q'、r = 2n/q' とすると、p' < q' < r' かつ 1/p' + 1/q' + 1/r' = p/2n + q/2n + r/2n = 1/2 となるので、( p', q', r' ) の組は (1) でもとめたものに限ります。以下、k を 1 以上の整数とします。
( p', q', r' ) = ( 3, 7, 42 ) のとき、n = 21k ならば p = 14k, q = 6k, r = k で p + q + r = 21k なので成り立ちます。
( p', q', r' ) = ( 3, 8, 24 ) のとき、n = 12k ならば p = 8k, q = 3k, r = k で p + q + r = 12k なので成り立ちます。
( p', q', r' ) = ( 3, 9, 18 ) のとき、n = 9k ならば p = 6k, q = 2k, r = k で p + q + r = 9k なので成り立ちます。
( p', q', r' ) = ( 3, 10, 15 ) のとき、n = 15k ならば p = 10k, q = 3k, r = 2k で p + q + r = 15k なので成り立ちます。
( p', q', r' ) = ( 4, 5, 20 ) のとき、n = 10k ならば p = 5k, q = 4k, r = k で p + q + r = 10k なので成り立ちます。
( p', q', r' ) = ( 4, 6, 12 ) のとき、n = 6k ならば p = 3k, q = 2k, r = k で p + q + r = 6k なので成り立ちます。
すなわち、n = 6k, 9k, 10k, 12k, 15k, 21k のとき p + q + r = n を満たす ( p, q, r ) の組が存在することになります。これらの最初公倍数は 2・2・3・3・5・7k = 1260k で、このとき f(n) = 6 となります。よって、M = 6 で、最小の数は 1260 です。
2017年03月18日
名大入試問題 2017 (5)
歯医者で検診がありました。結果、虫歯が一本。治療が必要ということで憂うつです。
2017 年名大入試文系の問題です。去年と同様、全体的に文系のほうが難しいと感じました。
-----
a を正の定数とする。2 次関数 f(x) = ax2 と 3 次関数 g(x) x( x - 4 )2 について、次の問に答えよ。
(1) 関数 y = g(x) について、極値を求め、そのグラフを描け。
(2) 2 つの曲線 y = f(x) と y = g(x) は相異なる 3 点で交わることを示せ。
(3) 2 つの曲線 y = f(x) と y = g(x) で囲まれた 2 つの部分の面積が等しくなるように a の値を定めよ。またそのとき、2 つの曲線の交点の x 座標を求めよ。
(1) g(x) = x( x - 4 )2 より
g'(x) = ( x - 4 )2 + 2x( x - 4 )
= ( x - 4 )( 3x - 4 )
なので、x = 4, 4/3 のとき極値になります。g(4) = 0, g(4/3) = 256/27 で増減表は
なのでグラフは下図のようになります。
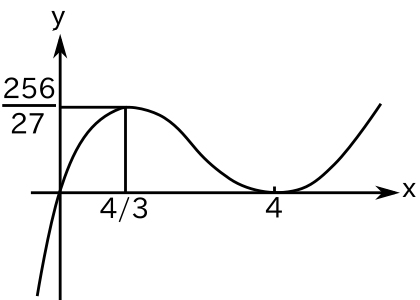
(2) f(x) = g(x) のとき、x( x - 4 )2 = ax2 より明らかに x = 0 を買いに持ちます。
x ≠ 0 のとき、両辺を x で割って ( x - 4 )2 = ax より
x2 - ( a + 8 )x + 16 = 0
の判別式 D を求めると
D = ( a + 8 )2 - 64 = a2 + 16a
となり、a は正の定数なので D > 0 より実数解は 2 つ存在します。従って、命題が成り立ちます。
(3) 2 つの解を r, s ( 但し r < s ) としたとき、
∫{0→s} x( x - 4 )2 - ax2 dx = 0
が成り立てばよいので、上式の左辺を計算すると
(左辺) = ∫{0→s} x3 - 8x2 + 16x - ax2 dx
= [ (1/4)x4 - (8/3)x3 + 8x2 - (a/3)x3 ]{0→s}
= (1/4)s4 - (8/3)s3 + 8s2 - (a/3)s3 = 0
となります。s ≠ 0 より左辺を s2 / 12 で割って
3s2 - ( 4a + 32 )s + 96 = 0
より a = (3/4)s + 24/s - 8 になります。r, s の値を計算すると
[ ( a + 8 ) ± ( a2 + 16a )1/2 ] / 2 で s は符号が + の方なので、
1/s = 2 / [ ( a + 8 ) ± ( a2 + 16a )1/2 ]
= [ ( a + 8 ) - ( a2 + 16a )1/2 ] / 32
より
a = (3/8)[ ( a + 8 ) + ( a2 + 16a )1/2 ] + (3/4)[ ( a + 8 ) - ( a2 + 16a )1/2 ] - 8
= (9/8)( a + 8 ) - (3/8)( a2 + 16a )1/2 - 8
となります。式を変形して
(1/8)a + 1 = (3/8)( a2 + 16a )1/2
より両辺に 8 を描けて 2 乗すると
( a + 8 )2 = 9( a2 + 16a )
式を整理して
a2 + 16a - 8 = 0
となります。従って
a = -8 ± 6√2
で a > 0 より a = -8 + 6√2 となります。このとき、r, s は
{ [ ( -8 + 6√2 ) + 8 ] ± [ ( -8 + 6√2 )2 + 16( -8 + 6√2 ) ]1/2 } / 2
= ( 6√2 ± √8 ) / 2 = 2√2, 4√2
と求められます。
2017 年名大入試文系の問題です。去年と同様、全体的に文系のほうが難しいと感じました。
-----
a を正の定数とする。2 次関数 f(x) = ax2 と 3 次関数 g(x) x( x - 4 )2 について、次の問に答えよ。
(1) 関数 y = g(x) について、極値を求め、そのグラフを描け。
(2) 2 つの曲線 y = f(x) と y = g(x) は相異なる 3 点で交わることを示せ。
(3) 2 つの曲線 y = f(x) と y = g(x) で囲まれた 2 つの部分の面積が等しくなるように a の値を定めよ。またそのとき、2 つの曲線の交点の x 座標を求めよ。
(1) g(x) = x( x - 4 )2 より
g'(x) = ( x - 4 )2 + 2x( x - 4 )
= ( x - 4 )( 3x - 4 )
なので、x = 4, 4/3 のとき極値になります。g(4) = 0, g(4/3) = 256/27 で増減表は
| x | 0 | 4/3 | 4 | ||||
|---|---|---|---|---|---|---|---|
| g(x) | - | 0 | + | 256/27 | + | 0 | - |
| g'(x) | + | 0 | - | 0 | + | ||
なのでグラフは下図のようになります。

(2) f(x) = g(x) のとき、x( x - 4 )2 = ax2 より明らかに x = 0 を買いに持ちます。
x ≠ 0 のとき、両辺を x で割って ( x - 4 )2 = ax より
x2 - ( a + 8 )x + 16 = 0
の判別式 D を求めると
D = ( a + 8 )2 - 64 = a2 + 16a
となり、a は正の定数なので D > 0 より実数解は 2 つ存在します。従って、命題が成り立ちます。
(3) 2 つの解を r, s ( 但し r < s ) としたとき、
∫{0→s} x( x - 4 )2 - ax2 dx = 0
が成り立てばよいので、上式の左辺を計算すると
(左辺) = ∫{0→s} x3 - 8x2 + 16x - ax2 dx
= [ (1/4)x4 - (8/3)x3 + 8x2 - (a/3)x3 ]{0→s}
= (1/4)s4 - (8/3)s3 + 8s2 - (a/3)s3 = 0
となります。s ≠ 0 より左辺を s2 / 12 で割って
3s2 - ( 4a + 32 )s + 96 = 0
より a = (3/4)s + 24/s - 8 になります。r, s の値を計算すると
[ ( a + 8 ) ± ( a2 + 16a )1/2 ] / 2 で s は符号が + の方なので、
1/s = 2 / [ ( a + 8 ) ± ( a2 + 16a )1/2 ]
= [ ( a + 8 ) - ( a2 + 16a )1/2 ] / 32
より
a = (3/8)[ ( a + 8 ) + ( a2 + 16a )1/2 ] + (3/4)[ ( a + 8 ) - ( a2 + 16a )1/2 ] - 8
= (9/8)( a + 8 ) - (3/8)( a2 + 16a )1/2 - 8
となります。式を変形して
(1/8)a + 1 = (3/8)( a2 + 16a )1/2
より両辺に 8 を描けて 2 乗すると
( a + 8 )2 = 9( a2 + 16a )
式を整理して
a2 + 16a - 8 = 0
となります。従って
a = -8 ± 6√2
で a > 0 より a = -8 + 6√2 となります。このとき、r, s は
{ [ ( -8 + 6√2 ) + 8 ] ± [ ( -8 + 6√2 )2 + 16( -8 + 6√2 ) ]1/2 } / 2
= ( 6√2 ± √8 ) / 2 = 2√2, 4√2
と求められます。
2017年03月12日
名大入試問題 2017 (4)
暑さ寒さも彼岸までとは言いますが、来週になれば暖かくなるのでしょうかね。
少し前に「ブラック・ジャック」の 1, 2 巻を買いました。昔の単行本のやつです。まだ買えるんですねこれ。
久しぶりに読みましたがやっぱり面白いです。続けてほしくなりましたが、コンプリートしようとすると結構お金かかるんですよね。どうしましょうか。
2017 年の名大入試問題の理系最後の問題です。次回から文系に移ります。
-----
n を自然数とする。0 でない複素数からなる集合 M が次の条件 (I), (II), (III) を満たしている。
(I) 集合 M は n 個の要素からなる。
(II) 集合 M の要素 z に対して 1 / z と -z はともに集合 M の要素である。
(III) 集合 M の要素 z, w に対して、その積 zw は集合 M の要素である。ただし、z = w の場合も含める。
このとき、次の問に答えよ。
(1) 1 および -1 は集合 M の要素であることを示せ。
(2) n は偶数であることを示せ。
(3) n = 4 のとき、集合 M は一通りに定まることを示し、その要素をすべて求めよ。
(3) n = 6 のとき、集合 M は一通りに定まることを示し、その要素をすべて求めよ。
(1) 集合 M のある要素 z に対して (II) より 1 / z は M の要素なので、(III) より z と 1 / z の積 1 は必ず集合 M の要素となります。また、(II) より -z も M の要素なので、(III) より -z と 1 / z の積 -1 も M の要素です。
(2) (1) より { 1, -1 } は必ず集合 M の要素となるので、M の一つの要素を z としたとき -1 との積 -z が必ず M に存在します。0 を含まないことから z ≠ -z かつ集合 M の異なる二つの要素 z1, z2 に対して -z1 ≠ -z2 なので、集合 M の要素は { z, -z } のペアをちょうど複数個持つことになり、n は偶数となります。
(3) { 1, -1 } は必ず M にあるので、残り 2 つの要素は ±1 とは異なるある複素数 z に対して [ z, 1 / z, -z } で表され、z ≠ -z より 1 / z は z, -z のいずれかと等しいことになります。z = 1 / z のとき z2 = 1 より z = ±1 なので条件を満たしません。-z = 1 / z のとき z2 = -1 となり、z = i より 4 つの要素 { 1, -1, i, -i } が決まります。
(4) ±1 とは異なるある複素数 z に対して条件 (III) より z2 も M の要素となります。z2 = 1 のとき z = ±1 であり条件を満たしません。また、z2 = -1 のとき z = i なので、これは n = 4 の場合に該当します。z2 = ±z のとき z = ±1 なのでこれらも除外すると、z2 は新たな要素であることになります。従って、{ 1, -1, z, -z, z2, -z2 } は集合 M の要素の一部を表し、その他に ±1 / z, ±1 / z2 も集合 M に含まれます。
1 / z = ±z のときは z2 = ±1 となりこれは n = 2, 4 の場合に該当します。
1 / z = z2 のとき z3 = 1 より 1 以外の解は z = ( -1 ± √3i ) / 2 となります。このとき、1 / z = 2 / ( -1 ± √3i ) = ( -1 ∓√3i ) / 2 = z2 であり、1 / z2 = 2 / ( -1 ∓√3i ) = ( -1 ±√3i ) / 2 = z となります。
1 / z = -z2 のとき z3 = -1 より -1 以外の解は z = ( 1 ± √3i ) / 2 となります。このとき、1 / z = 2 / ( 1 ± √3i ) = ( 1 ∓√3i ) / 2 = z2 であり、1 / z2 = 2 / ( 1 ∓√3i ) = ( 1 ±√3i ) / 2 = z となります。
よって、n = 6 のときは { 1, -1, ( 1 ± √3i ) / 2, ( -1 ± √3i ) / 2 } のみとなります。
少し前に「ブラック・ジャック」の 1, 2 巻を買いました。昔の単行本のやつです。まだ買えるんですねこれ。
久しぶりに読みましたがやっぱり面白いです。続けてほしくなりましたが、コンプリートしようとすると結構お金かかるんですよね。どうしましょうか。
2017 年の名大入試問題の理系最後の問題です。次回から文系に移ります。
-----
n を自然数とする。0 でない複素数からなる集合 M が次の条件 (I), (II), (III) を満たしている。
(I) 集合 M は n 個の要素からなる。
(II) 集合 M の要素 z に対して 1 / z と -z はともに集合 M の要素である。
(III) 集合 M の要素 z, w に対して、その積 zw は集合 M の要素である。ただし、z = w の場合も含める。
このとき、次の問に答えよ。
(1) 1 および -1 は集合 M の要素であることを示せ。
(2) n は偶数であることを示せ。
(3) n = 4 のとき、集合 M は一通りに定まることを示し、その要素をすべて求めよ。
(3) n = 6 のとき、集合 M は一通りに定まることを示し、その要素をすべて求めよ。
(1) 集合 M のある要素 z に対して (II) より 1 / z は M の要素なので、(III) より z と 1 / z の積 1 は必ず集合 M の要素となります。また、(II) より -z も M の要素なので、(III) より -z と 1 / z の積 -1 も M の要素です。
(2) (1) より { 1, -1 } は必ず集合 M の要素となるので、M の一つの要素を z としたとき -1 との積 -z が必ず M に存在します。0 を含まないことから z ≠ -z かつ集合 M の異なる二つの要素 z1, z2 に対して -z1 ≠ -z2 なので、集合 M の要素は { z, -z } のペアをちょうど複数個持つことになり、n は偶数となります。
(3) { 1, -1 } は必ず M にあるので、残り 2 つの要素は ±1 とは異なるある複素数 z に対して [ z, 1 / z, -z } で表され、z ≠ -z より 1 / z は z, -z のいずれかと等しいことになります。z = 1 / z のとき z2 = 1 より z = ±1 なので条件を満たしません。-z = 1 / z のとき z2 = -1 となり、z = i より 4 つの要素 { 1, -1, i, -i } が決まります。
(4) ±1 とは異なるある複素数 z に対して条件 (III) より z2 も M の要素となります。z2 = 1 のとき z = ±1 であり条件を満たしません。また、z2 = -1 のとき z = i なので、これは n = 4 の場合に該当します。z2 = ±z のとき z = ±1 なのでこれらも除外すると、z2 は新たな要素であることになります。従って、{ 1, -1, z, -z, z2, -z2 } は集合 M の要素の一部を表し、その他に ±1 / z, ±1 / z2 も集合 M に含まれます。
1 / z = ±z のときは z2 = ±1 となりこれは n = 2, 4 の場合に該当します。
1 / z = z2 のとき z3 = 1 より 1 以外の解は z = ( -1 ± √3i ) / 2 となります。このとき、1 / z = 2 / ( -1 ± √3i ) = ( -1 ∓√3i ) / 2 = z2 であり、1 / z2 = 2 / ( -1 ∓√3i ) = ( -1 ±√3i ) / 2 = z となります。
1 / z = -z2 のとき z3 = -1 より -1 以外の解は z = ( 1 ± √3i ) / 2 となります。このとき、1 / z = 2 / ( 1 ± √3i ) = ( 1 ∓√3i ) / 2 = z2 であり、1 / z2 = 2 / ( 1 ∓√3i ) = ( 1 ±√3i ) / 2 = z となります。
よって、n = 6 のときは { 1, -1, ( 1 ± √3i ) / 2, ( -1 ± √3i ) / 2 } のみとなります。
2017年03月11日
名大入試問題 2017 (3)
今日は 3 月 11 日です。
Yahoo で「3.11」と検索すると、10 円が寄付されます。但し、3 月 11 日中だけです。今なら間に合いますよ。
2017 年名大入試問題の 3 問目です。そういえば、合格発表がすでにあったようですね。
-----
xyz 空間の 2 点 A( 0, 0, 2 ), P( a, b, 0 ) を通る直線を l とする。また、点 ( 2, 0, 0 ) を中心都市、半径が √2 である球面を S で表し、S のうち z 座標が z > 0 を満たす部分を T とする。このとき、次の問に答えよ。
(1) l 上に点 Q がある。実数 t を [AQ] = t[AP] ( [XY]は二点 X, Y を結ぶベクトルを表す ) で定めるとき、点 Q の座標を a, b, t を使って表せ。
(2) l が S と相異なる 2 点で交わるような実数 a, b に関する条件を求め、ab 平面上に図示せよ。
(3) l が T と相異なる 2 点で交わるような実数 a, b に関する条件を求め、ab 平面上に図示せよ。
(1) 図より Q( at, bt, 2 - 2t ) です。
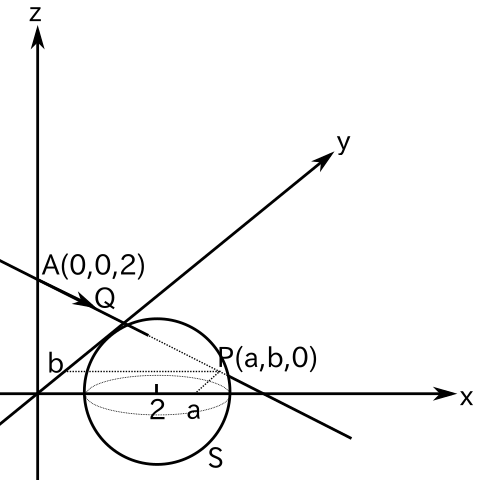
(2) l と S の交点を Q とすると、( at - 2 )2 + ( bt )2 + ( 2 - 2t )2 = 2 が成り立ちます。これを変形すると
( a2 + b2 + 4 )t2 - ( 4a + 8 )t + 6 = 0
これが異なる実数解を持つためには判別式 D > 0 である必要があります。従って
D = ( 4a + 8 )2 - 24( a2 + b2 + 4 )
= -8a2 + 64a - 24b2 - 32 > 0 より
a2 - 8a + 3b2 + 4 < 0
( a - 4 )2 + 3b2 < 12 が条件となります。
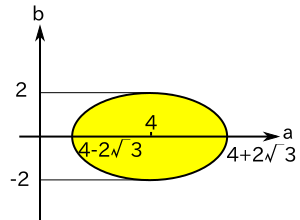
(3) P が球の内部にある場合、l は T 上の 1 点と、S の z ≤ 0 の領域の 1 点で交差することになります。従ってこの範囲では成り立たず、( a - 2 )2 + b2 > 2 でなければなりません。
P が球の外部にある場合、S の z > 0 の領域の 2 点で交差する場合が成り立つ範囲となります。f(t) = ( a2 + b2 + 4 )t2 - ( 4a + 8 )t + 6 としたとき、|AQ| < |AP| となることからこの関数は t < 1 の領域で実数解を持つので
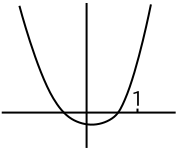
(i) f(1) > 0
(ii) f'(1) > 0
の二つが成り立つことになります。(i) より
f(1) = ( a2 + b2 + 4 ) - ( 4a + 8 ) + 6 = ( a - 2 )2 + b2 - 2 > 0
なのでこれは先程求めた範囲に等しくなります。また、(ii) より
f'(1) = 2( a2 + b2 + 4 ) - ( 4a + 8 ) = 2( a - 1 )2 + 2b2 - 2 > 0
なので、( a - 1 )2 + b2 > 1 がもう一つの範囲となります。(2) の結果と合わせると、求める条件は
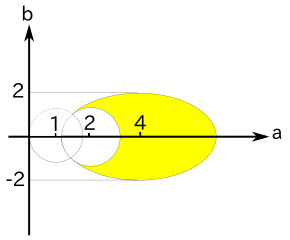
( a - 4 )2 + 3b2 < 12
( a - 2 )2 + b2 > 2
( a - 1 )2 + b2 > 1
となります。
( a - 4 )2 + 3b2 = 12 と ( a - 2 )2 + b2 = 2 の交点は ( a, b ) = ( 1, ±1 ) です。
また、( a - 2 )2 + b2 = 2 と ( a - 1 )2 + b2 = 1 の交点も ( a, b ) = ( 1, ±1 ) で、この 3 つの曲線は同じ点 ( a, b ) = ( 1, ±1 ) で交わります。それに注意して図示すると以下のようになります。
Yahoo で「3.11」と検索すると、10 円が寄付されます。但し、3 月 11 日中だけです。今なら間に合いますよ。
2017 年名大入試問題の 3 問目です。そういえば、合格発表がすでにあったようですね。
-----
xyz 空間の 2 点 A( 0, 0, 2 ), P( a, b, 0 ) を通る直線を l とする。また、点 ( 2, 0, 0 ) を中心都市、半径が √2 である球面を S で表し、S のうち z 座標が z > 0 を満たす部分を T とする。このとき、次の問に答えよ。
(1) l 上に点 Q がある。実数 t を [AQ] = t[AP] ( [XY]は二点 X, Y を結ぶベクトルを表す ) で定めるとき、点 Q の座標を a, b, t を使って表せ。
(2) l が S と相異なる 2 点で交わるような実数 a, b に関する条件を求め、ab 平面上に図示せよ。
(3) l が T と相異なる 2 点で交わるような実数 a, b に関する条件を求め、ab 平面上に図示せよ。
(1) 図より Q( at, bt, 2 - 2t ) です。

(2) l と S の交点を Q とすると、( at - 2 )2 + ( bt )2 + ( 2 - 2t )2 = 2 が成り立ちます。これを変形すると
( a2 + b2 + 4 )t2 - ( 4a + 8 )t + 6 = 0
これが異なる実数解を持つためには判別式 D > 0 である必要があります。従って
D = ( 4a + 8 )2 - 24( a2 + b2 + 4 )
= -8a2 + 64a - 24b2 - 32 > 0 より
a2 - 8a + 3b2 + 4 < 0
( a - 4 )2 + 3b2 < 12 が条件となります。

(3) P が球の内部にある場合、l は T 上の 1 点と、S の z ≤ 0 の領域の 1 点で交差することになります。従ってこの範囲では成り立たず、( a - 2 )2 + b2 > 2 でなければなりません。
P が球の外部にある場合、S の z > 0 の領域の 2 点で交差する場合が成り立つ範囲となります。f(t) = ( a2 + b2 + 4 )t2 - ( 4a + 8 )t + 6 としたとき、|AQ| < |AP| となることからこの関数は t < 1 の領域で実数解を持つので

(i) f(1) > 0
(ii) f'(1) > 0
の二つが成り立つことになります。(i) より
f(1) = ( a2 + b2 + 4 ) - ( 4a + 8 ) + 6 = ( a - 2 )2 + b2 - 2 > 0
なのでこれは先程求めた範囲に等しくなります。また、(ii) より
f'(1) = 2( a2 + b2 + 4 ) - ( 4a + 8 ) = 2( a - 1 )2 + 2b2 - 2 > 0
なので、( a - 1 )2 + b2 > 1 がもう一つの範囲となります。(2) の結果と合わせると、求める条件は
( a - 4 )2 + 3b2 < 12
( a - 2 )2 + b2 > 2
( a - 1 )2 + b2 > 1
となります。
( a - 4 )2 + 3b2 = 12 と ( a - 2 )2 + b2 = 2 の交点は ( a, b ) = ( 1, ±1 ) です。
また、( a - 2 )2 + b2 = 2 と ( a - 1 )2 + b2 = 1 の交点も ( a, b ) = ( 1, ±1 ) で、この 3 つの曲線は同じ点 ( a, b ) = ( 1, ±1 ) で交わります。それに注意して図示すると以下のようになります。

2017年03月11日
名大入試問題 2017 (2)
2017 年名大入試問題の二問目です。個人的には一番悩まされた問題です。
-----
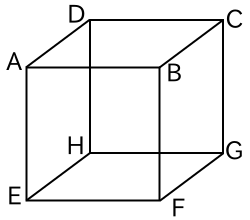
下図のような立方体を考える。この立方体の 8 つの頂点の上を点 P が次の規則で移動する。時刻 0 では点 P は頂点 A にいる。時刻が 1 増えるごとに点 P は、今いる頂点と辺で結ばれている頂点に等確率で移動する。例えば時刻 n で点 P が頂点 H にいるとすると、時刻 n + 1 では、それぞれ 1 / 3 の確率で頂点 D, E, G のいずれかにいる。自然数 n ≥ 1 に対して、(i) 点 P が時刻 n までの間一度も頂点 A に戻らず、かつ時刻 n で頂点 B, D, E のいずれかにいる確率を pn、(ii) 点 P が時刻 n までの間一度も頂点 A に戻らず、かつ時刻 n で頂点 C, F, H のいずれかにいる確率を qn、(iii) 点 P が時刻 n までの間一度も頂点 A に戻らず、かつ時刻 n で頂点 G にいる確率を rn とする。このとき、次の問に答えよ。
(1) p2, q2, r2 と p3, q3, r3 を求めよ。
(2) n ≥ 2 のとき、pn, qn, rn を求めよ。
(3) 自然数 m ≥ 1 に対して、点 P が時刻 2m で頂点 A に初めて戻る確率 sm を求めよ。
(4) 自然数 m ≥ 2 に対して、点 P が時刻 2m で頂点 A に戻るのがちょうど 2 回目となる確率を tm とする。このとき、tm < sm となる m をすべて求めよ。
(1) 時刻 1 で点 P は B, D, E のいずれかにいるので p1 = 1 です。時刻 2 では B, D, E から A に戻る確率が 1 / 3、C, F, H へ移動する確率が 2 / 3 なので p2 = 0, q2 = 2 / 3, r2 = 0 となります。時刻 3 では C, F, H から G へ移動する確率が 1 / 3、B, D, E へ戻る確率が 2 / 3 で、q2 = 2 / 3 だったので p3 = 2/3 x 2/3 = 4 / 9、q3 = 0、r3 = 2/3 x 1/3 = 2 / 9 となります。
(2) n = 2m ( m は 1 以上の整数 ) のとき、点 P は C, F, H のいずれかにあるので p2m = r2m = 0 になります。また、n = 2m - 1 のとき、点 P は C, F, H のいずれにもないので q2m-1 = 0 です。
時刻 2m + 1 のとき、C, F, H にいた点 P は 2 / 3 の確率で B, D, E へ、1 / 3 の確率で G へ移動するので p2m+1 = (2/3)q2m、r2m+1 = (1/3)q2m が成り立ちます。また、時刻 2m + 2 のとき、B, D, E にいた点 P は 2 / 3 の確率で C, F, H へ、1 / 3 の確率で A へ移動し、G にいた場合は必ず C, F, H に移動するので q2m+2 = (2/3)p2m+1 + r2m+1 となります。従って、
q2m+2 = (2/3)・(2/3)q2m + (1/3)q2m = (7/9)q2m より q2m = (2/3)(7/9)m-1
であり、
p2m+1 = (4/9)(7/9)m-1、r2m+1 = (2/9)(7/9)m-1
となります。
(3) 時刻 2 のときは、(1) で述べたように 1 / 3 になります。それ以降は、時刻 2m - 1 のときに B, D, E にある確率 p2m-1 = (4/9)(7/9)m-2 に、A に移る確率 1 / 3 を掛ければ求められ、sm = (4/27)(7/9)m-2 になります。
(4) B, D, E にいる場合を X、C, F, H にいる場合を Y で表すことにします。まず、t1 = 0 は明らかです。t2 は A→X→A→X→A と遷移する場合しかないので、 1/3 x 1/3 = 1 / 9 です。s2 = 4 / 27 なので t2 < s2 となります。t3 は以下の二通りの確率の和になります。
A→X→A→X→Y→X→A 1/3 x 2/3 x 2/3 x 1/3 = 4 / 81
A→X→Y→X→A→X→A 2/3 x 2/3 x 1/3 x 1/3 = 4 / 81
よって、t3 = 8 / 81 で、s3 = 28 / 243 より t3 < s3 です。t4 の場合、
(a) A→X→A→X→Y→{ X or G }→Y→X→A
(b) A→X→Y→X→A→X→Y→X→A
(c) A→X→Y→{ X or G }→Y→X→A→X→A
となりますが ( X or G はいずれかに遷移するという意味です )、(a) の場合 A→X→A の部分とそれ以降に分けて考えると、それぞれ初めて A に戻る確率 s1, s3 に等しいので 1/3 x (4/27)(7/9) = 28 / 729 です。同様に (b) は 4/27 x 4/27 = 16 / 729、(c) は (4/27)(7/9) x 1/3 = 28 / 729 で、合わせて 72 / 729 になります。s4 = 196 / 2187 なので t4 > s4 で m = 4 のときは成り立ちません。
m = 4 の結果から、m ≥ 4 の場合の tm の計算式が以下のようになることがわかります。
tm = (1/3)・(4/27)(7/9)m-3 + (4/27)・(4/27)(7/9)m-4 + (4/27)(7/9)・(4/27)(7/9)m-5 + ... + (4/27)(7/9)m-3・(1/3)
= (2/3)(4/27)(7/9)m-3 + (4/27)2( m - 3 )(7/9)m-4
> [ (2/3)(9/7) + (4/27)(9/7)2 ](4/27)(7/9)m-2
= (162/147)(4/27)(7/9)m-2 > sm
従って、条件を満たす m は 2, 3 になります。
-----
下図のような立方体を考える。この立方体の 8 つの頂点の上を点 P が次の規則で移動する。時刻 0 では点 P は頂点 A にいる。時刻が 1 増えるごとに点 P は、今いる頂点と辺で結ばれている頂点に等確率で移動する。例えば時刻 n で点 P が頂点 H にいるとすると、時刻 n + 1 では、それぞれ 1 / 3 の確率で頂点 D, E, G のいずれかにいる。自然数 n ≥ 1 に対して、(i) 点 P が時刻 n までの間一度も頂点 A に戻らず、かつ時刻 n で頂点 B, D, E のいずれかにいる確率を pn、(ii) 点 P が時刻 n までの間一度も頂点 A に戻らず、かつ時刻 n で頂点 C, F, H のいずれかにいる確率を qn、(iii) 点 P が時刻 n までの間一度も頂点 A に戻らず、かつ時刻 n で頂点 G にいる確率を rn とする。このとき、次の問に答えよ。
(1) p2, q2, r2 と p3, q3, r3 を求めよ。
(2) n ≥ 2 のとき、pn, qn, rn を求めよ。
(3) 自然数 m ≥ 1 に対して、点 P が時刻 2m で頂点 A に初めて戻る確率 sm を求めよ。
(4) 自然数 m ≥ 2 に対して、点 P が時刻 2m で頂点 A に戻るのがちょうど 2 回目となる確率を tm とする。このとき、tm < sm となる m をすべて求めよ。

(1) 時刻 1 で点 P は B, D, E のいずれかにいるので p1 = 1 です。時刻 2 では B, D, E から A に戻る確率が 1 / 3、C, F, H へ移動する確率が 2 / 3 なので p2 = 0, q2 = 2 / 3, r2 = 0 となります。時刻 3 では C, F, H から G へ移動する確率が 1 / 3、B, D, E へ戻る確率が 2 / 3 で、q2 = 2 / 3 だったので p3 = 2/3 x 2/3 = 4 / 9、q3 = 0、r3 = 2/3 x 1/3 = 2 / 9 となります。
(2) n = 2m ( m は 1 以上の整数 ) のとき、点 P は C, F, H のいずれかにあるので p2m = r2m = 0 になります。また、n = 2m - 1 のとき、点 P は C, F, H のいずれにもないので q2m-1 = 0 です。
時刻 2m + 1 のとき、C, F, H にいた点 P は 2 / 3 の確率で B, D, E へ、1 / 3 の確率で G へ移動するので p2m+1 = (2/3)q2m、r2m+1 = (1/3)q2m が成り立ちます。また、時刻 2m + 2 のとき、B, D, E にいた点 P は 2 / 3 の確率で C, F, H へ、1 / 3 の確率で A へ移動し、G にいた場合は必ず C, F, H に移動するので q2m+2 = (2/3)p2m+1 + r2m+1 となります。従って、
q2m+2 = (2/3)・(2/3)q2m + (1/3)q2m = (7/9)q2m より q2m = (2/3)(7/9)m-1
であり、
p2m+1 = (4/9)(7/9)m-1、r2m+1 = (2/9)(7/9)m-1
となります。
(3) 時刻 2 のときは、(1) で述べたように 1 / 3 になります。それ以降は、時刻 2m - 1 のときに B, D, E にある確率 p2m-1 = (4/9)(7/9)m-2 に、A に移る確率 1 / 3 を掛ければ求められ、sm = (4/27)(7/9)m-2 になります。
(4) B, D, E にいる場合を X、C, F, H にいる場合を Y で表すことにします。まず、t1 = 0 は明らかです。t2 は A→X→A→X→A と遷移する場合しかないので、 1/3 x 1/3 = 1 / 9 です。s2 = 4 / 27 なので t2 < s2 となります。t3 は以下の二通りの確率の和になります。
A→X→A→X→Y→X→A 1/3 x 2/3 x 2/3 x 1/3 = 4 / 81
A→X→Y→X→A→X→A 2/3 x 2/3 x 1/3 x 1/3 = 4 / 81
よって、t3 = 8 / 81 で、s3 = 28 / 243 より t3 < s3 です。t4 の場合、
(a) A→X→A→X→Y→{ X or G }→Y→X→A
(b) A→X→Y→X→A→X→Y→X→A
(c) A→X→Y→{ X or G }→Y→X→A→X→A
となりますが ( X or G はいずれかに遷移するという意味です )、(a) の場合 A→X→A の部分とそれ以降に分けて考えると、それぞれ初めて A に戻る確率 s1, s3 に等しいので 1/3 x (4/27)(7/9) = 28 / 729 です。同様に (b) は 4/27 x 4/27 = 16 / 729、(c) は (4/27)(7/9) x 1/3 = 28 / 729 で、合わせて 72 / 729 になります。s4 = 196 / 2187 なので t4 > s4 で m = 4 のときは成り立ちません。
m = 4 の結果から、m ≥ 4 の場合の tm の計算式が以下のようになることがわかります。
tm = (1/3)・(4/27)(7/9)m-3 + (4/27)・(4/27)(7/9)m-4 + (4/27)(7/9)・(4/27)(7/9)m-5 + ... + (4/27)(7/9)m-3・(1/3)
= (2/3)(4/27)(7/9)m-3 + (4/27)2( m - 3 )(7/9)m-4
> [ (2/3)(9/7) + (4/27)(9/7)2 ](4/27)(7/9)m-2
= (162/147)(4/27)(7/9)m-2 > sm
従って、条件を満たす m は 2, 3 になります。
2017年03月05日
名大入試問題 2017 (1)
3 月になりました。だいぶ暖かくなりましたね。
本日、「アルゴリズムのコーナー」を更新しました。内容は予定通り「自己組織化写像(SOM)」です。今回はかなりボリュームが少なくなりました。他に面白いネタがあれば追加したいのですが、あいにく今のところ思い浮かびません。結構おもしろいアルゴリズムで、他にもいろいろな応用があると思うのですが。。。
新聞に載っていた名大の入試問題を今年も解いてみました。まずは一問目から。今回は解答もチェックしていますので答えは合ってます。
-----
不等式 0 < a < 1 を満たす定数 a に対して、曲線 C : y = a - 1 - log x ( x > 0 ) を考える。s を正の定数とし、曲線 C 上の点 P( s, a - 1 - log s ) における接線が x 軸、y 軸と交わる点をそれぞれ ( u(s), 0 ), ( 0, v(s) ) とする。このとき、次の問いに答えよ。必要があれば、lim{x→0} x log x = 0 を証明なしで使ってよい (2017年 名大)。
(1) 関数 u(s), v(s) を s の式で表せ。
(2) 関数 t = u(s), t = v(s) の 2 つのグラフを、領域・凹凸および交点の座標に注意して、同じ st 平面上に図示せよ。
(3) 関数 t = u(s), t = v(s) の 2 つのグラフで囲まれた図形を t 軸のまわりに 1 回転させてできる立体の体積を求めよ。
(1) y' = -1 / x より P の接線は
y = (-1/s)( x - s ) + a - 1 - log s = (-1/s)x + a - log s
となります。y = 0 のとき
x = s( a - log s ) より u(s) = s( a - log s )
x = 0 のとき
y = a - log s より v(s) = a - log s
となります。
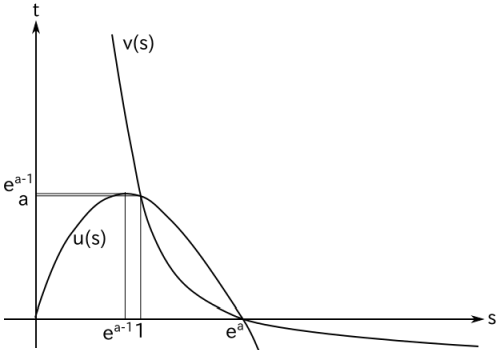
(2) u'(s) = a - log s - 1, u''(s) = -1 / s < 0 より u(s) は 0 < s < ea-1 で増加、s = ea-1 のとき極値をとり、s > ea-1 で減少します。また、s = 0, ea のとき u(s) = 0 となります。
v'(s) = -1/s < 0, v''(s) = 1 / s2 > 0 v(s) は単調減少で下に凸であり、s = ea のとき v(s) = 0 です。
u(s) と v(s) の交点は、s( a - log s ) = a - log s より a - log s ≠ 0 のとき s = 1、a - log s = 0 のとき s = ea です。よって、グラフは下図のようになります。
(3) t = v(s) = a - log s より s = ea-t なので、v(s) を t 軸のまわりに回転させたときの 0 ≤ t ≤ a での回転体の体積は
π∫{0→a} e2a-2t dt
= π[ (-1/2)e2a-2t ]{0→a}
= π( -1/2 + e2a / 2 )
= (π/2)( e2a - 1 )
となります。また、t = u(s) s( a - log s ) より dt = ( a - log s - 1 )ds、t = 0 のとき s = ea、t = a のとき s = 1 なので、回転体の体積は
π∫{0→a} s2 dt
= π∫{ea→1} s2( a - log s - 1 ) ds
= π{ [ (1/3)( a - 1 )s3 ]{ea→1} - ∫{ea→1} s2 log s ds }
で計算できます。
∫{ea→1} s2 log s ds
= [ (1/3)s3log s ]{ea→1} - (1/3)∫{ea→1} s2 ds
= -(1/3)ae3a - (1/3)[ (1/3)s3 ]{ea→1}
= -(1/3)ae3a - 1 / 9 + (1/9)e3a
なので、
π∫{0→a} s2 dt
= π{ (1/3)( a - 1 )( 1 - e3a ) + (1/3)ae3a + 1 / 9 - (1/9)e3a }
= π[ (2/9)e3a - 2 / 9 + (1/3)a ]
となり、求める体積は
= π[ (2/9)e3a - 2 / 9 + (1/3)a ] - (π/2)( e2a - 1 )
= (π/18)( 4e3a - 9e2a + 6a + 5 )
となります。
回転体の体積の求め方をすっかり忘れておりました。ググって調べたのは内緒です。
本日、「アルゴリズムのコーナー」を更新しました。内容は予定通り「自己組織化写像(SOM)」です。今回はかなりボリュームが少なくなりました。他に面白いネタがあれば追加したいのですが、あいにく今のところ思い浮かびません。結構おもしろいアルゴリズムで、他にもいろいろな応用があると思うのですが。。。
新聞に載っていた名大の入試問題を今年も解いてみました。まずは一問目から。今回は解答もチェックしていますので答えは合ってます。
-----
不等式 0 < a < 1 を満たす定数 a に対して、曲線 C : y = a - 1 - log x ( x > 0 ) を考える。s を正の定数とし、曲線 C 上の点 P( s, a - 1 - log s ) における接線が x 軸、y 軸と交わる点をそれぞれ ( u(s), 0 ), ( 0, v(s) ) とする。このとき、次の問いに答えよ。必要があれば、lim{x→0} x log x = 0 を証明なしで使ってよい (2017年 名大)。
(1) 関数 u(s), v(s) を s の式で表せ。
(2) 関数 t = u(s), t = v(s) の 2 つのグラフを、領域・凹凸および交点の座標に注意して、同じ st 平面上に図示せよ。
(3) 関数 t = u(s), t = v(s) の 2 つのグラフで囲まれた図形を t 軸のまわりに 1 回転させてできる立体の体積を求めよ。
(1) y' = -1 / x より P の接線は
y = (-1/s)( x - s ) + a - 1 - log s = (-1/s)x + a - log s
となります。y = 0 のとき
x = s( a - log s ) より u(s) = s( a - log s )
x = 0 のとき
y = a - log s より v(s) = a - log s
となります。
(2) u'(s) = a - log s - 1, u''(s) = -1 / s < 0 より u(s) は 0 < s < ea-1 で増加、s = ea-1 のとき極値をとり、s > ea-1 で減少します。また、s = 0, ea のとき u(s) = 0 となります。
v'(s) = -1/s < 0, v''(s) = 1 / s2 > 0 v(s) は単調減少で下に凸であり、s = ea のとき v(s) = 0 です。
u(s) と v(s) の交点は、s( a - log s ) = a - log s より a - log s ≠ 0 のとき s = 1、a - log s = 0 のとき s = ea です。よって、グラフは下図のようになります。

(3) t = v(s) = a - log s より s = ea-t なので、v(s) を t 軸のまわりに回転させたときの 0 ≤ t ≤ a での回転体の体積は
π∫{0→a} e2a-2t dt
= π[ (-1/2)e2a-2t ]{0→a}
= π( -1/2 + e2a / 2 )
= (π/2)( e2a - 1 )
となります。また、t = u(s) s( a - log s ) より dt = ( a - log s - 1 )ds、t = 0 のとき s = ea、t = a のとき s = 1 なので、回転体の体積は
π∫{0→a} s2 dt
= π∫{ea→1} s2( a - log s - 1 ) ds
= π{ [ (1/3)( a - 1 )s3 ]{ea→1} - ∫{ea→1} s2 log s ds }
で計算できます。
∫{ea→1} s2 log s ds
= [ (1/3)s3log s ]{ea→1} - (1/3)∫{ea→1} s2 ds
= -(1/3)ae3a - (1/3)[ (1/3)s3 ]{ea→1}
= -(1/3)ae3a - 1 / 9 + (1/9)e3a
なので、
π∫{0→a} s2 dt
= π{ (1/3)( a - 1 )( 1 - e3a ) + (1/3)ae3a + 1 / 9 - (1/9)e3a }
= π[ (2/9)e3a - 2 / 9 + (1/3)a ]
となり、求める体積は
= π[ (2/9)e3a - 2 / 9 + (1/3)a ] - (π/2)( e2a - 1 )
= (π/18)( 4e3a - 9e2a + 6a + 5 )
となります。
回転体の体積の求め方をすっかり忘れておりました。ググって調べたのは内緒です。





