2017年03月05日
名大入試問題 2017 (1)
3 月になりました。だいぶ暖かくなりましたね。
本日、「アルゴリズムのコーナー」を更新しました。内容は予定通り「自己組織化写像(SOM)」です。今回はかなりボリュームが少なくなりました。他に面白いネタがあれば追加したいのですが、あいにく今のところ思い浮かびません。結構おもしろいアルゴリズムで、他にもいろいろな応用があると思うのですが。。。
新聞に載っていた名大の入試問題を今年も解いてみました。まずは一問目から。今回は解答もチェックしていますので答えは合ってます。
-----
不等式 0 < a < 1 を満たす定数 a に対して、曲線 C : y = a - 1 - log x ( x > 0 ) を考える。s を正の定数とし、曲線 C 上の点 P( s, a - 1 - log s ) における接線が x 軸、y 軸と交わる点をそれぞれ ( u(s), 0 ), ( 0, v(s) ) とする。このとき、次の問いに答えよ。必要があれば、lim{x→0} x log x = 0 を証明なしで使ってよい (2017年 名大)。
(1) 関数 u(s), v(s) を s の式で表せ。
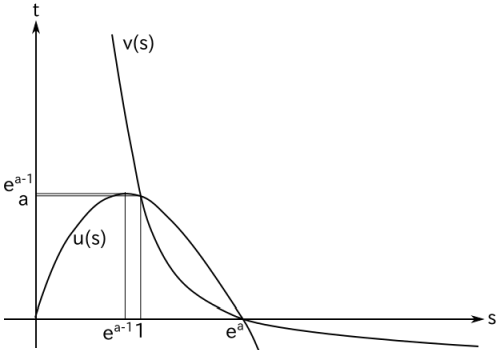
(2) 関数 t = u(s), t = v(s) の 2 つのグラフを、領域・凹凸および交点の座標に注意して、同じ st 平面上に図示せよ。
(3) 関数 t = u(s), t = v(s) の 2 つのグラフで囲まれた図形を t 軸のまわりに 1 回転させてできる立体の体積を求めよ。
(1) y' = -1 / x より P の接線は
y = (-1/s)( x - s ) + a - 1 - log s = (-1/s)x + a - log s
となります。y = 0 のとき
x = s( a - log s ) より u(s) = s( a - log s )
x = 0 のとき
y = a - log s より v(s) = a - log s
となります。
(2) u'(s) = a - log s - 1, u''(s) = -1 / s < 0 より u(s) は 0 < s < ea-1 で増加、s = ea-1 のとき極値をとり、s > ea-1 で減少します。また、s = 0, ea のとき u(s) = 0 となります。
v'(s) = -1/s < 0, v''(s) = 1 / s2 > 0 v(s) は単調減少で下に凸であり、s = ea のとき v(s) = 0 です。
u(s) と v(s) の交点は、s( a - log s ) = a - log s より a - log s ≠ 0 のとき s = 1、a - log s = 0 のとき s = ea です。よって、グラフは下図のようになります。
(3) t = v(s) = a - log s より s = ea-t なので、v(s) を t 軸のまわりに回転させたときの 0 ≤ t ≤ a での回転体の体積は
π∫{0→a} e2a-2t dt
= π[ (-1/2)e2a-2t ]{0→a}
= π( -1/2 + e2a / 2 )
= (π/2)( e2a - 1 )
となります。また、t = u(s) s( a - log s ) より dt = ( a - log s - 1 )ds、t = 0 のとき s = ea、t = a のとき s = 1 なので、回転体の体積は
π∫{0→a} s2 dt
= π∫{ea→1} s2( a - log s - 1 ) ds
= π{ [ (1/3)( a - 1 )s3 ]{ea→1} - ∫{ea→1} s2 log s ds }
で計算できます。
∫{ea→1} s2 log s ds
= [ (1/3)s3log s ]{ea→1} - (1/3)∫{ea→1} s2 ds
= -(1/3)ae3a - (1/3)[ (1/3)s3 ]{ea→1}
= -(1/3)ae3a - 1 / 9 + (1/9)e3a
なので、
π∫{0→a} s2 dt
= π{ (1/3)( a - 1 )( 1 - e3a ) + (1/3)ae3a + 1 / 9 - (1/9)e3a }
= π[ (2/9)e3a - 2 / 9 + (1/3)a ]
となり、求める体積は
= π[ (2/9)e3a - 2 / 9 + (1/3)a ] - (π/2)( e2a - 1 )
= (π/18)( 4e3a - 9e2a + 6a + 5 )
となります。
回転体の体積の求め方をすっかり忘れておりました。ググって調べたのは内緒です。
本日、「アルゴリズムのコーナー」を更新しました。内容は予定通り「自己組織化写像(SOM)」です。今回はかなりボリュームが少なくなりました。他に面白いネタがあれば追加したいのですが、あいにく今のところ思い浮かびません。結構おもしろいアルゴリズムで、他にもいろいろな応用があると思うのですが。。。
新聞に載っていた名大の入試問題を今年も解いてみました。まずは一問目から。今回は解答もチェックしていますので答えは合ってます。
-----
不等式 0 < a < 1 を満たす定数 a に対して、曲線 C : y = a - 1 - log x ( x > 0 ) を考える。s を正の定数とし、曲線 C 上の点 P( s, a - 1 - log s ) における接線が x 軸、y 軸と交わる点をそれぞれ ( u(s), 0 ), ( 0, v(s) ) とする。このとき、次の問いに答えよ。必要があれば、lim{x→0} x log x = 0 を証明なしで使ってよい (2017年 名大)。
(1) 関数 u(s), v(s) を s の式で表せ。
(2) 関数 t = u(s), t = v(s) の 2 つのグラフを、領域・凹凸および交点の座標に注意して、同じ st 平面上に図示せよ。
(3) 関数 t = u(s), t = v(s) の 2 つのグラフで囲まれた図形を t 軸のまわりに 1 回転させてできる立体の体積を求めよ。
(1) y' = -1 / x より P の接線は
y = (-1/s)( x - s ) + a - 1 - log s = (-1/s)x + a - log s
となります。y = 0 のとき
x = s( a - log s ) より u(s) = s( a - log s )
x = 0 のとき
y = a - log s より v(s) = a - log s
となります。
(2) u'(s) = a - log s - 1, u''(s) = -1 / s < 0 より u(s) は 0 < s < ea-1 で増加、s = ea-1 のとき極値をとり、s > ea-1 で減少します。また、s = 0, ea のとき u(s) = 0 となります。
v'(s) = -1/s < 0, v''(s) = 1 / s2 > 0 v(s) は単調減少で下に凸であり、s = ea のとき v(s) = 0 です。
u(s) と v(s) の交点は、s( a - log s ) = a - log s より a - log s ≠ 0 のとき s = 1、a - log s = 0 のとき s = ea です。よって、グラフは下図のようになります。

(3) t = v(s) = a - log s より s = ea-t なので、v(s) を t 軸のまわりに回転させたときの 0 ≤ t ≤ a での回転体の体積は
π∫{0→a} e2a-2t dt
= π[ (-1/2)e2a-2t ]{0→a}
= π( -1/2 + e2a / 2 )
= (π/2)( e2a - 1 )
となります。また、t = u(s) s( a - log s ) より dt = ( a - log s - 1 )ds、t = 0 のとき s = ea、t = a のとき s = 1 なので、回転体の体積は
π∫{0→a} s2 dt
= π∫{ea→1} s2( a - log s - 1 ) ds
= π{ [ (1/3)( a - 1 )s3 ]{ea→1} - ∫{ea→1} s2 log s ds }
で計算できます。
∫{ea→1} s2 log s ds
= [ (1/3)s3log s ]{ea→1} - (1/3)∫{ea→1} s2 ds
= -(1/3)ae3a - (1/3)[ (1/3)s3 ]{ea→1}
= -(1/3)ae3a - 1 / 9 + (1/9)e3a
なので、
π∫{0→a} s2 dt
= π{ (1/3)( a - 1 )( 1 - e3a ) + (1/3)ae3a + 1 / 9 - (1/9)e3a }
= π[ (2/9)e3a - 2 / 9 + (1/3)a ]
となり、求める体積は
= π[ (2/9)e3a - 2 / 9 + (1/3)a ] - (π/2)( e2a - 1 )
= (π/18)( 4e3a - 9e2a + 6a + 5 )
となります。
回転体の体積の求め方をすっかり忘れておりました。ググって調べたのは内緒です。
この記事へのトラックバックURL
http://fussy.mediacat-blog.jp/t121109
※このエントリーではブログ管理者の設定により、ブログ管理者に承認されるまでコメントは反映されません





