Fussy's Diary

先週末は歓迎会で飲んでました。

ケーブルテレビが光ファイバーに配線切替されるということで工事の下見がありました。メールアドレスが有料になるものの月額はそのままで通信速度が速くなるということで非常にオトクな話です。しかし、ショックだったのが無線 LAN 機能標準装備ということ。ルータが最近故障して買い直したばかりだったので非常に損した気分です。もう少し故障するのが遅ければ。。。

「数学問題bot」から東大の問題です。かなり悩みました。例によって合っている保証はありません。

-----

各世代ごとに、各個体が他の個体とは独立に、確率 p [ 0 < p < 1 ] で 1 個、確率 1 - p で 2 個の新しい個体を次の世代に残し、それ自身消滅する細胞がある。第 0 世代に 1 個だった細胞が第 n [ n ∈ N ] 世代に m 個になる確率を Pn(m) と書く。Pn(1), Pn(2), Pn(3) を求めよ ( 84 東大 )

下図は、第 4 世代まで、3 個まで分裂するときの確率を表したものです。



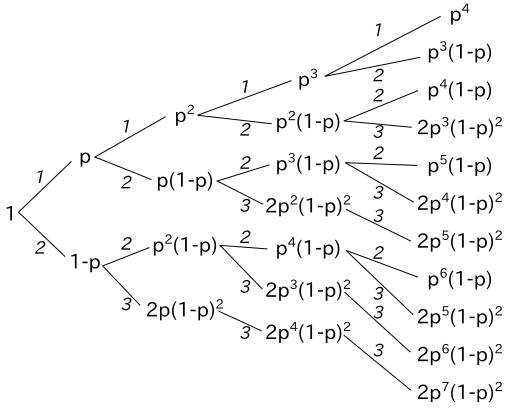
前の世代が 1 個の場合、次の世代では 1 個か 2 個のいずれかにしかなりません。次の世代が 1 個になる確率は前の確率に p を掛けたものになります。また、2 個になる確率は前の確率に p( 1 - p ) を掛けたものになります。
前の世代が 2 個の場合、次の世代では 2, 3, 4 個のいずれかになります。次の世代が 2 個になる確率は前の確率に p² を掛けたものになります。また、3 個になる確率は前の確率に 2p( 1 - p ) を掛けたものになります。
前の世代が 3 個の場合、次の世代では 3 から 6 個までのいずれかになります。次の世代が 3 個になる確率は前の確率に p³ を掛けたものになります。

1 個の個体を残す事象を A、2 個の個体を残す事象を B とします。n 回目で 1 つだけになるのは常に事象 A が発生した場合なので、その確率は pⁿ です。よって、Pn(1) = pⁿ となります。

n 回目で 2 個となるのは、n - 1 回目で 1 個であった場合に事象 B が発生する場合と、2 個であった場合に A, B が各々発生した場合に限られます。従って、各回について 2 個になる場合は 1 つずつ増え、1 個から 2 個に変化した場合、それまでは p^n-1 の確率で発生していたので p^n-1( p - 1 ) の確率になります。また、2 個のままである場合、それまでの確率に p² を掛けた確率になります。

上図から、Pn(2) = ( p^n-1 + pⁿ + ... + p^2n-2 )( 1 - p ) と仮定してみます。このとき、P1(2) = 1 - p で成り立ちます。
n + 1 回目では、各事象に対して p² を掛けたものに 1 個から 2 個に増えた場合の確率 pⁿ( 1 - p ) を加えた値になるので

Pn+1(2)
= pⁿ( 1 - p ) + p²( p^n-1 + pⁿ + ... + p^2n-2 )( 1 - p )
= ( pⁿ + pⁿ⁺¹ + pⁿ⁺² + ... + p^2(n+1)-2 )( 1 - p )

となり、帰納法により正しいことがわかります。

Pn(2) = ( p^n-1 + pⁿ + ... + p^2n-2 )( 1 - p )
pPn(2) = ( pⁿ + pⁿ⁺¹ + ... + p^2n-1 )( 1 - p ) より

( 1 - p )Pn(2) = ( p^n-1 - p^2n-1 )( 1 - p )

よって Pn(2) = p^n-1 - p^2n-1 = p^n-1( 1 - pⁿ ) となります。

n 回目で 3 個となるのは、n - 1 回目で 2 個であった場合に A, B の両方が発生した場合と、3 個であった場合に全てにおいて A が発生した場合に限られます。n 回目で 2 個から 3 個になる確率は 2 個になる確率 p^n-2( 1 - p^n-1 ) に 2p( 1 - p ) を掛けることで求められ、3 個のままである確率は Pn-1(3) に p³ を掛けることで求められるので、次の漸化式が成り立つことになります。

Pn(3) = p³Pn-1(3) + 2p^n-1( 1 - p )( 1 - p^n-1 )

これを解くと、

Pn(3)
= p³Pn-1(3) + 2p^n-1( 1 - p )( 1 - p^n-1 )
= p³[ p³Pn-2(3) + 2p^n-2( 1 - p )( 1 - p^n-2 ) ] + 2p^n-1( 1 - p )( 1 - p^n-1 )
= p⁶Pn-2(3) + 2pⁿ⁺¹( 1 - p )( 1 - p^n-2 ) + 2p^n-1( 1 - p )( 1 - p^n-1 )
= p⁶[ p³Pn-3(3) + 2p^n-3( 1 - p )( 1 - p^n-3 ) ] + 2pⁿ⁺¹( 1 - p )( 1 - p^n-2 ) + 2p^n-1( 1 - p )( 1 - p^n-1 )
= p⁹Pn-3(3) + 2pⁿ⁺³( 1 - p )( 1 - p^n-3 ) + 2pⁿ⁺¹( 1 - p )( 1 - p^n-2 ) + 2p^n-1( 1 - p )( 1 - p^n-1 )
= ...
= p^3(n-1)P1(3) + 2^3p-5( 1 - p )² + ... + 2pⁿ⁺¹( 1 - p )( 1 - p^n-2 ) + 2p^n-1( 1 - p )( 1 - p^n-1 )
= Σ_k{1→n-1}( 2p^3n-3-2k( 1 - p )( 1 - p^k ) )

となります。式を展開して

Pn(3) = ( 1 - p )Σ_k{1→n-1}( 2p^3n-3-2k - 2p^3n-3-k ) ≡ ( 1 - p )( S1 + S2 )

とすると、

S1 = 2p^3n-5 + 2p^3n-7 + ... + 2p^n-1
p²S1 = 2p^3n-3 + 2p^3n-5 + ... + 2pⁿ⁺¹

で、辺々引いて

( 1 - p² )S1 = 2p^n-1 - 2p^3n-3
S1 = 2p^n-1( 1 - p^2n-2 ) / ( 1 - p² )

となります。また、

S2 = 2p^3n-4 + 2p^3n-5 + ... + 2p^2n-2
pS2 = 2p^3n-3 + 2p^3n-4 + ... + 2p^2n-1

で、辺々引いて

( 1 - p )S2 = 2p^2n-2 - 2p^3n-3
S2 = 2p^2n-2( 1 - p^n-1 ) / ( 1 - p )

なので、

Pn(3)
= 2p^n-1( 1 - p^2n-2 ) / ( 1 + p ) - 2p^2n-2( 1 - p^n-1 )
= 2p^n-1[ ( 1 - p^2n-2 ) - ( 1 + p )( p^n-1 - p^2n-2 ] / ( 1 + p )
= 2p^n-1( 1 - p^2n-2 - p^n-1 + p^2n-2 - pⁿ + p^2n-1 ) / ( 1 + p )
= 2p^n-1[ ( 1 - p^n-1 ) - pⁿ( 1 - p^n-1 ) ] / ( 1 + p )
= 2p^n-1( 1 - pⁿ )( 1 - p^n-1 ) / ( 1 + p )

となります。