Fussy's Diary

めっきり寒くなってきました。今年も残り二ヶ月ですね。

クラスタリングの一つ、SOM ( Self-organizing maps ) のサンプル・プログラムを作成してみました。SOM を使うことで、高次元のデータを二次元マップ上に写像して視覚的に分類することが可能になります。
紹介しているサイトを見ると、理解しやすい色のクラスタリングが例としてよく挙がっていますが、巡回サラリーマン問題の近似解を求める応用例を見つけてさっそく試してみました。二次元データを二次元マップに写像することで目的を達成することができます。



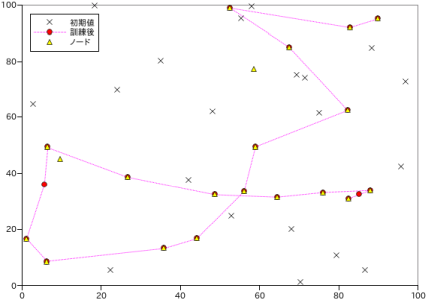
初期値 "×" を与えて訓練すると、"△" のノードに次第に近づいていきます。真の解ではないですが、割りといい結果が得られているのではないかと思います。この使い方を見つけてから SOM を使うのがなかなか面白くなってきました。

クラスタリングには他にも凝集型クラスタリングや K-平均法、EM アルゴリズムなどがありますが、現在、順番にサンプル・プログラムを作成しようとしているところです。年内にできれば一度更新したいですね。  

「アルゴリズムのコーナー」の「画像処理」の章を全てリニューアルしました。主にサンプル・プログラムの見直しを行っています。

「シーム・カービング」は試してみて非常に楽しいアルゴリズムなので、時間があれば他にもいろいろと試してみたいです。また、そのうちに更新を行うかもしれませんが、当分は先の話になりそうです。まだ作ってみたいものは他にもたくさんありますし。

「数学問題bot」から不等式の問題です。最初は手も足も出ない状態でしたが、ふと思い立った方法でなんとか証明してみました。例によって合っている保証はありません。

-----

不等式 (1/2)･(3/4)･(5/6)･ ... ･(999999/1000000) < 1/1000 を示せ ( 第 14 回シュプリンガー数学コンテスト )

命題の証明の前に、二つの補題を証明しておきます。

(補題 1) ( 1 - 1 / n )^-n は単調減少で lim{n→∞} ( 1 - 1 / n )^-n = e

f(x) = ln ( 1 - 1 / x )^-x ( x > 1 ) とすると、

f(x) = -x ln ( 1 - 1 / x ) = -x ln ( x - 1 ) + x ln x

f'(x) = -ln ( x - 1 ) - x / ( x - 1 ) + ln x + 1 = -ln ( x - 1 ) + ln x - 1 / ( x - 1 )

f''(x) = -1 / ( x - 1 ) + 1 / x + 1 / ( x - 1 )²
= [ -x( x - 1 ) + ( x - 1 )² + x ] / x( x - 1 )²
= ( -x² + x + x² - 2x + 1 + x ) / x( x - 1 )²
= 1 / x( x - 1 )² > 0

よって、f'(x) は単調増加です。また、

f'(x) = -ln ( x - 1 ) + ln x - 1 / ( x - 1 )
= ln ( 1 + 1 / ( x - 1 ) ) - 1 / ( x - 1 )
→ 0 ( x → ∞ )

なので f'(x) < 0 となり、f(x) は単調減少となることから ( 1 - 1 / n )^-n も単調減少となります。

ネイピア数の定義より lim{n→∞} ( 1 + 1 / n )ⁿ = e であることを利用すると、

( 1 + 1 / n )ⁿ / ( 1 - 1 / n )^-n
= ( 1 - 1 / n² )ⁿ
= 1 - n( 1 / n² ) + (1/2)n( n - 1 )( 1 / n² )² - ... + (-1)^k_nC_k( 1 / n² )^k + ... → 1 ( n → ∞ )

より lim{n→∞} ( 1 - 1 / n )^-n = e となります。

(補題 2) 関数 ln x に対し、下図において A > B が常に成り立つ



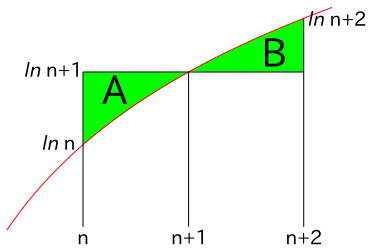
A = ln ( n + 1 ) - ∫{n→n+1} ln x dx
B = ∫{n+1→n+2} ln x dx - ln ( n + 1 )

より

A - B
= ln ( n + 1 ) - ∫{n→n+1} ln x dx - ∫{n+1→n+2} ln x dx + ln ( n + 1 )
= 2ln ( n + 1 ) - ∫{n→n+2} ln x dx
= 2ln ( n + 1 ) - [ x ln x ]{n→n+2} + [ x ]{n→n+2}
= 2ln ( n + 1 ) - ( n + 2 ) ln ( n + 2 ) + n ln n + 2
= ln ( n + 1 )²nⁿe² / ( n + 2 )ⁿ⁺²
= ln [ n / ( n + 2 ) ]ⁿ[ ( n + 1 ) / ( n + 2 ) ]²e²

となります。ここで

[ n / ( n + 2 ) ]ⁿ
= { [ 1 - 2 / ( n + 2 ) ]^(n+2)/2 }²[ ( n + 2 ) / n ]²

より

A - B = ln { [ 1 - 2 / ( n + 2 ) ]^(n+2)/2 }²[ ( n + 1 ) / n ]²e²

となり、補題 1 から { [ 1 - 2 / ( n + 2 ) ]^-(n+2)/2 }² は単調減少で → e² ( n→∞ ) だから、{ [ 1 - 2 / ( n + 2 ) ]^(n+2)/2 }² は単調増加で → 1 / e² ( n→∞ ) となります。また、[ ( n + 1 ) / n ]² → 1 ( n→∞ ) なので、A - B → ln ( 1 / e² )・1・e² = 0 ( n→∞ ) が成り立ちます。

n = 1 のとき、

A - B = ln ( 1 / 3 )( 2 / 3 )²e² = ln ( 4 / 27 )e² > ln ( 4 / 27 )( 2.7 )² = ln 1.08 & gt; 0

なので、A - B が n の増加に対して単調減少であれば常に正であることになります。そこで、

f(x) = 2ln ( x + 1 ) - ( x + 2 ) ln ( x + 2 ) + x ln x + 2 ( x ≥ 1 )

とすると、

f'(x)
= 2 / ( x + 1 ) - ln ( x + 2 ) - 1 + ln x + 1
= 2 / ( x + 1 ) - ln ( x + 2 ) + ln x

f''(x)
= -2 / ( x + 1 )² - 1 / ( x + 2 ) + 1 / x
= [ -2x( x + 2 ) - x( x + 1 )² + ( x + 1 )²( x + 2 ) ] / x( x + 1 )²( x + 2 )
= [ -2x² - 4x + 2( x + 1 )² ] / x( x + 1 )²( x + 2 )
= 2 / x( x + 1 )²( x + 2 ) > 0

なので f'(x) は単調増加で、x = 1 のとき f'(1) = 1 - ln 3 > 0、f'(x) = 2 / ( x + 1 ) + ln ( 1 - 2 / ( x + 2 ) ) → 0 ( x→∞ ) だから、f'(x) < 0 が成り立ちます。よって f(x) は単調減少で、f(x) > 0 が常に成り立つことが証明されました。

(証明)

ln (1/2)･(3/4)･(5/6)･ ... ･(999999/1000000) = ( ln 1 + ln 3 + ... + ln 999999 ) - ( ln 2 + ln 4 + ... + ln 1000000 )

と変形できるので、左辺の二つの項についてその大きさを調べてみます。



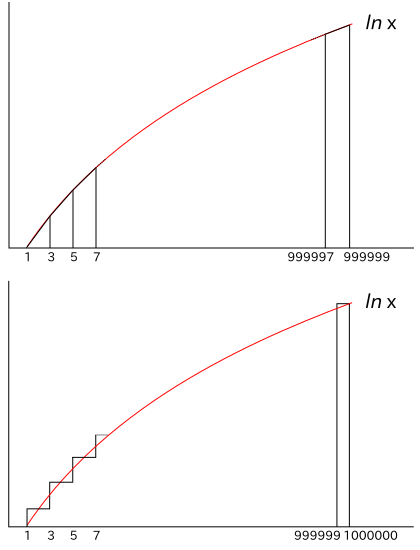
上図の上側の ln x と台形との面積の大きさを比較すると、

2( ln 1 + ln 3 ) / 2 + 2( ln 3 + ln 5 ) / 2 + ... 2( ln 999997 + ln 999999 ) / 2 < ∫{1→999999} ln x dx

が成り立ちます。この式は

ln1 + 2( ln 3 + ln 5 + ... + ln 999997 ) + ln 999999 < ∫{1→999999} ln x dx

と変形できて、ln 1 = 0 だから

ln1 + ln 3 + ln 5 + ... + ln 999997 + ln 999999 < (1/2)( ∫{1→999999} ln x dx + ln 999999 )

が成り立ちます。また、図の下側と補題 2 から

2 ln 2 + 2 ln 4 + 2 ln 6 + ... + ln 1000000 > ∫{1→1000000} ln x dx

なので、

ln 2 + ln 4 + ln 6 + ... + ln 1000000 > (1/2)( ∫{1→1000000} ln x dx + ln 1000000 )

となります。よって、

( ln 1 + ln 3 + ... + ln 999999 ) - ( ln 2 + ln 4 + ... + ln 1000000 ) < (1/2)( ∫{1→999999} ln x dx + ln 999999 - ∫{1→1000000} ln x dx + ln 1000000 )

ここで 1000000 = M, 999999 = m として右辺を変形すると

(右辺) = (1/2)[ ln ( m / M ) - ∫{m→M} ln x dx ]

∫{m→M} ln x dx
= [ x ln x ]{m→M} - &int{m→M} dx
= ln ( M^M / m^m ) - ( M - m )
= ln ( M^M / m^m ) - 1

よって

(右辺)
= (1/2)[ ln ( m / M ) - ln ( M^M / m^m ) + 1 )
= (1/2) ln ( m^mme / M^MM )
= (1/2) ln ( ( m / M )^M( e / M ) )
= (1/2) ln ( ( 1 - 1 / M )^M( e / M ) )

となります。補題 1 から

( 1 - 1 / M )^M = 1 / ( 1 - 1 / M )^-M → 1 / e ( M→∞ )

であり、( 1 - 1 / M )^-M は単調減少だから ( 1 - 1 / M )^-M > e より ( 1 - 1 / M )^M < 1 / e となって、

( ln 1 + ln 3 + ... + ln 999999 ) - ( ln 2 + ln 4 + ... + ln 1000000 )
< (1/2)( ∫{1→999999} ln x dx + ln 999999 - ∫{1→1000000} ln x dx + ln 1000000 )
< (1/2)ln 1 / 1000000 = ln ( 1 / 1000 )

よって、不等式が証明されました。
  

少し前から、クラスタリングの勉強を始めてます。昔に覚えた手法も含めてもう一度基礎からやり直しで、ようやく少しずつ理解が進んできた感じです。で、SOM ( 自己組織化写像 ) のサンプル・プログラムを作成したのですが、思ったような結果が得られず苦戦しています。いつ頃公開できるかは未定ですが、とりあえず次のテーマはこのあたりにするつもりです。

数学問題bot から拾った問題です。例によって合っている保証はありません。

-----

n を 2 以上の整数とする。1 つのサイコロを n 回投げ、第 1 回目から第 n 回目までに出た目の最大公約数を G とする。G の期待値を n の式で表せ ( 07 大阪 )

サイコロを n 回投げたときの目の並べ方は 6ⁿ 通りあります。その中で G = 2 となるのは、目が 2, 4, 6 のいずれかで、全ての目が 4 のみまたは 6 のみの場合を除いたときなので、その並べ方は 3ⁿ - 2 通りになります。同様に、G = 3 となるのは目が 3, 6 のいずれかで、すべての目が 6 のみの場合を除いたときなのでその並べ方は 2ⁿ - 1 通りです。G = 4, 5, 6 になるのは、それぞれ目が 4, 5, 6 のみの場合だけなので各々 1 通りのみで、残りは G = 1 の場合で 6ⁿ - ( 3ⁿ - 2 ) - ( 2ⁿ - 1 ) - 3 = 6ⁿ - 3ⁿ - 2ⁿ 通りになります。従って G の期待値は

[ 2・( 3ⁿ - 2 ) + 3・( 2ⁿ - 1 ) + 4 + 5 + 6 + ( 6ⁿ - 3ⁿ - 2ⁿ ) ] / 6ⁿ
= ( 3ⁿ + 2ⁿ⁺¹ + 6ⁿ + 8 ) / 6ⁿ
= ( 1 / 2 )ⁿ + 2( 1 / 3 )ⁿ + 8( 1 / 6 )ⁿ + 1

となります。n → ∞ のとき期待値が 1 に収束するのは、一回でも 1 の目が出れば G = 1 となることからも納得のできる結果です。  

今日は涼しい一日でした。これくらいの気温がちょうどいいですね。これ以上は寒くなってほしくないです。本当に。

家の中で久しぶりにゴキブリに遭遇して速攻で殺虫剤で撃退しました。まだ成虫にはなっていないゴキブリでしたが、やっぱり気持ち悪いです。
ヤモリでも蛾でも素手で捕まえて外に逃がすことができますがゴキブリだけはダメです。あのテカテカした表面がどうも苦手なんですよね。苦手じゃないという人のほうが圧倒的に少ないとは思いますが。
しかし、元々は森で暮らしていた昆虫だと思うので、そういうところで遭遇していればまた違った見方になるのかもしれません。どんな昆虫でも家の中で見かけたら違和感はありますからね。そういう意味では自然に合った姿形なのかもしれません。案外、人間の方が自然には馴染めない姿だったりして。  

いろいろあってドタバタした週末でした。

自分が病気になったわけではないのですが、訳あってこのところ大きな病院へ行く機会が多くなりました。しばらく病室にいると、いろんな患者さんがいることに気付きます。頻繁にナースコールする人、点滴の針を抜いてしまい怒られている人、勝手に病室を抜け出して注意される人などなど。当然、みんな病人なのでどこか痛んだり調子が悪くなったりするわけで、その度に看護師さんが飛んできます。
二つの病院に交互に行くことになったわけですが、それぞれ巡回の数とか食事の献立とか様々です。しかし、共通点はとにかく多忙であるということ。確かに、医師や看護師は重労働だと改めて思いました。それでも、定期的に見回りに来てもらえるので非常にありがたいと感じます。

自分は入院をした経験がありません。これからもそんな経験をしなくて済めばいいんですけど。やはり健康が一番です。