2019年03月17日
もうすぐ春分の日
今週は春分の日がありますね。いよいよ春到来ですか。
今回も名大の入試問題を解いてみたいと思います。今年ではなく去年の問題から選んでみました。
ちなみに、たいていは問題文の短いものを選択しています。図入りのものなんかは画像を作らなきゃならないのでよほどのことがない限りパスしてます。
-----
■ p を素数、a, b を整数とする。このとき、次の問に答えよ ( 2018 年 名大 )。
(1) ( a + b )p - ap - bp は p で割り切れることを示せ。
(2) ( a + 2 )p - ap は偶数であることを示せ。
(3) ( a + 2 )p - ap を 2p で割ったときの余りを求めよ。
(1) 二項定理より
( a + b )p - ap - bp = Σk{1→p-1}( pCkakbp-k )
なので、pCk ( k = 1, 2, ... p - 1 ) が p で割り切れることを示せば十分です。pCk = p! / k!( p - k )! より分子は p を素因数に持ちますが、分母は持ちません。p は素数なので分母にあるすべての素因数と互いに素です。pCk は整数なので、pCk は p で割り切れることになります。
(2) ( a + 2 )p - ap = 2Σk{0→p-1}( pCkak2p-k-1 )
より、偶数であることが示されます。
(3) (2) で示した式と (1) の結果より、k が 1 から p - 1 までの項は 2p で割り切れるので、2pC0a02p-1 = 2p を 2p で割ったときの余りを求めればよいことになります。p = 2 のときは明らかに 0 なので、奇素数の場合を考えます。
2p = ( 1 + 1 )p
と表せることから、( 1 + 1 )p - 1 - 1 は (1) より p で割り切れ、かつ偶数であるので、2p - 2 は 2p で割り切れることになり、2p を 2p で割った余りは 2 となります。
今回も名大の入試問題を解いてみたいと思います。今年ではなく去年の問題から選んでみました。
ちなみに、たいていは問題文の短いものを選択しています。図入りのものなんかは画像を作らなきゃならないのでよほどのことがない限りパスしてます。
-----
■ p を素数、a, b を整数とする。このとき、次の問に答えよ ( 2018 年 名大 )。
(1) ( a + b )p - ap - bp は p で割り切れることを示せ。
(2) ( a + 2 )p - ap は偶数であることを示せ。
(3) ( a + 2 )p - ap を 2p で割ったときの余りを求めよ。
(1) 二項定理より
( a + b )p - ap - bp = Σk{1→p-1}( pCkakbp-k )
なので、pCk ( k = 1, 2, ... p - 1 ) が p で割り切れることを示せば十分です。pCk = p! / k!( p - k )! より分子は p を素因数に持ちますが、分母は持ちません。p は素数なので分母にあるすべての素因数と互いに素です。pCk は整数なので、pCk は p で割り切れることになります。
(2) ( a + 2 )p - ap = 2Σk{0→p-1}( pCkak2p-k-1 )
より、偶数であることが示されます。
(3) (2) で示した式と (1) の結果より、k が 1 から p - 1 までの項は 2p で割り切れるので、2pC0a02p-1 = 2p を 2p で割ったときの余りを求めればよいことになります。p = 2 のときは明らかに 0 なので、奇素数の場合を考えます。
2p = ( 1 + 1 )p
と表せることから、( 1 + 1 )p - 1 - 1 は (1) より p で割り切れ、かつ偶数であるので、2p - 2 は 2p で割り切れることになり、2p を 2p で割った余りは 2 となります。
2019年03月10日
久々に入試問題
このところ雨が多くなってきました。季節も春に移りつつあるようです。
新聞に載っていた今年の名大の入試問題をいくつか解いてみました。久々に紹介してみたいと思います。
-----
正の整数 n の正の平方根 √n は整数ではなく、それを 10 進法で表すと、小数第 1 位は 0 であり、第 2 位は 0 以外の数であるとする ( 2019 年 名大 )。
(1) このような n の中で最小のものを求めよ。
(2) このような n を小さいものから順に並べたときに 10 番目にくるものを求めよ。
(1) √n は整数ではなく、小数第 1 位が 0 なので、ある整数 m を使って m.01 以上で m.1 より小さい数として表すことができます。
m = 1 のとき、1.12 = 1.21 < 2 なので、2, 3 は非該当です。
m = 2 のとき、2.12 = 4.41 < 5 なので、5, 6, 7, 8 は非該当です。
m = 3 のとき、3.12 = 9.61 < 10 なので、10~15 は非該当です。
m = 4 のとき、4.12 = 16.81 < 17 なので、17~24 は非該当です。
m = 5 のとき、5.12 = 26.01 > 26 で、5.012 = 25.1001 < 26 なので 26 が最小となります。
m.1 の平方値の増え方には規則性があります。実際、
( m + 0.1 )2 = m2 + 0.2m + 0.01
( m + 1.1 )2 = m2 + 2.2m + 1.21
なので、m が 1 増えることに m.12 は 2m + 1.2 ずつ増えます。また
( m + 0.01 )2 = m2 + 0.02m + 0.0001
なので、分解して計算すると計算が少し楽になります。
(2) 5.12 < 27 なので、27~35 は非該当です。
m = 6 のとき、6.12 = 37.21 > 37 で、6.012 = 36.1201 < 37 なので 37 が 2 番目となります。
m = 7 のとき、7.12 = 50.41 > 50 で、7.012 = 49.1401 < 50 なので 50 が 3 番目となります。
m = 8 のとき、8.12 = 65.61 > 65 で、8.012 = 64.1601 < 65 なので 65 が 4 番目となります。
m = 9 のとき、9.12 = 82.81 > 82 で、9.012 = 81.1801 < 82 なので 82 が 5 番目となります。
m = 10 のとき、10.12 = 102.01 > 102 で、10.012 = 100.2001 < 101 なので 101, 102 で 6, 7 番目となります。
m = 11 のとき、11.12 = 123.21 > 123 で、11.012 = 121.2201 < 122 なので 122, 123 で 8, 9 番目となります。
m = 12 のとき、12.12 = 146.41 > 146 で、12.012 = 144.2401 < 145 なので 145 が 10 番目となります。
計算さえ間違えなければ割と簡単に解ける問題だと思います。新聞の解答はもう少し凝った方法で解いているようでした。
新聞に載っていた今年の名大の入試問題をいくつか解いてみました。久々に紹介してみたいと思います。
-----
正の整数 n の正の平方根 √n は整数ではなく、それを 10 進法で表すと、小数第 1 位は 0 であり、第 2 位は 0 以外の数であるとする ( 2019 年 名大 )。
(1) このような n の中で最小のものを求めよ。
(2) このような n を小さいものから順に並べたときに 10 番目にくるものを求めよ。
(1) √n は整数ではなく、小数第 1 位が 0 なので、ある整数 m を使って m.01 以上で m.1 より小さい数として表すことができます。
m = 1 のとき、1.12 = 1.21 < 2 なので、2, 3 は非該当です。
m = 2 のとき、2.12 = 4.41 < 5 なので、5, 6, 7, 8 は非該当です。
m = 3 のとき、3.12 = 9.61 < 10 なので、10~15 は非該当です。
m = 4 のとき、4.12 = 16.81 < 17 なので、17~24 は非該当です。
m = 5 のとき、5.12 = 26.01 > 26 で、5.012 = 25.1001 < 26 なので 26 が最小となります。
m.1 の平方値の増え方には規則性があります。実際、
( m + 0.1 )2 = m2 + 0.2m + 0.01
( m + 1.1 )2 = m2 + 2.2m + 1.21
なので、m が 1 増えることに m.12 は 2m + 1.2 ずつ増えます。また
( m + 0.01 )2 = m2 + 0.02m + 0.0001
なので、分解して計算すると計算が少し楽になります。
(2) 5.12 < 27 なので、27~35 は非該当です。
m = 6 のとき、6.12 = 37.21 > 37 で、6.012 = 36.1201 < 37 なので 37 が 2 番目となります。
m = 7 のとき、7.12 = 50.41 > 50 で、7.012 = 49.1401 < 50 なので 50 が 3 番目となります。
m = 8 のとき、8.12 = 65.61 > 65 で、8.012 = 64.1601 < 65 なので 65 が 4 番目となります。
m = 9 のとき、9.12 = 82.81 > 82 で、9.012 = 81.1801 < 82 なので 82 が 5 番目となります。
m = 10 のとき、10.12 = 102.01 > 102 で、10.012 = 100.2001 < 101 なので 101, 102 で 6, 7 番目となります。
m = 11 のとき、11.12 = 123.21 > 123 で、11.012 = 121.2201 < 122 なので 122, 123 で 8, 9 番目となります。
m = 12 のとき、12.12 = 146.41 > 146 で、12.012 = 144.2401 < 145 なので 145 が 10 番目となります。
計算さえ間違えなければ割と簡単に解ける問題だと思います。新聞の解答はもう少し凝った方法で解いているようでした。
2017年11月26日
勤労感謝の日
先週は「勤労感謝の日」で一日お休みでした。
今年の祝日はあと一日、「天皇誕生日」を残すのみとなりました。気がつけばもうすぐ 12 月。寒さも厳しくなってきて、冬が苦手な自分にとってはつらい時期となりました。
「数学問題bot(個人用)」から同志社大学の問題です。例によって合っている保証なしです。
-----
m, n は自然数とする ( m > n )。「m と n が互いに素」⇔「2m - 1 と 2n - 1 が互いに素」を示せ ( 同志社 )
2m - 1 と 2n - 1 の差分は以下のように計算できます。
( 2m - 1 ) - ( 2n - 1 )
= 2m - 2n
= 2n[ 2m-n - 1 ]
m, n は互いに素であることから m - n は m, n の因数を持たず ( もし持つならば、m の因数を G、m = Gm'、m - n = GK としたとき m - n = Gm' - n = GK より n = G( m' - K ) となり m, n は共通の因数を持つので矛盾 )、m, n, m - n はそれぞれ互いに素になります。
m > n, m > m - n より、n と m - n に対して同様の操作を行うと、n > m - n の場合、 n, m - n, n - ( m - n ) = 2n - m は互いに素であり、n > m - n, n > 2n - m です。さらに m - n, 2n - m に対してこの操作を行います。以下、最大数 ( 最初は m ) を除いた 2 数でこの操作を繰り返すと、常に値は小さくなっていき最終的には差が 1 になります。この 2 数を M, N ( M > N )とすると M - N = 1 で
( 2M - 1 ) - ( 2N - 1 )
= 2M - 2N
= 2N[ 2M-N - 1 ] = 2N
であり、2M - 1 と 2N - 1 は奇数なので 2 を因数として持たず、従って互いに素です。遡って M + N, M, N では
( 2M+N - 1 ) - ( 2M - 1 ) = 2M( 2N - 1 )
より
2M+N - 1 = 2M( 2N - 1 ) + ( 2M - 1 )
であり、2M - 1 と 2N - 1 は互いに素で 2M は偶数なので 2M - 1 と 2M( 2N - 1 ) は互いに素なので、2M+N - 1, 2M - 1, 2N - 1 は それぞれ互いに素です。これを繰り返していくと最終的に 2m - 1 と 2n - 1 は互いに素になります。
ちなみに m = 7, n = 2 のとき
( 27 - 1 ) - ( 22 - 1 ) = 22( 25 - 1 ) [ 127 - 3 = 4・31 ) ]
( 25 - 1 ) - ( 22 - 1 ) = 22( 23 - 1 ) [ 31 - 3 = 4・7 ]
( 23 - 1 ) - ( 22 - 1 ) = 22 [ 7 - 3 = 4 ]
で 3, 7, 31, 127 は全て互いに素になります。
2m - 1, 2n - 1 はそれぞれ 1 のみからなる m, n 桁の二進数で表すことができます。m, n が互いに素でない時、m, n の共通因数を G とすると、2m - 1, 2n - 1 はどちらも 2G - 1 ( G 桁の 1 のみからなる二進数 ) で割り切れます。よって 2m - 1, 2n - 1 は共通因数 2G - 1 を持ち、互いに素ではありません。この対偶として、2m - 1, 2n - 1 が互いに素なら m, n は互いに素です。
今年の祝日はあと一日、「天皇誕生日」を残すのみとなりました。気がつけばもうすぐ 12 月。寒さも厳しくなってきて、冬が苦手な自分にとってはつらい時期となりました。
「数学問題bot(個人用)」から同志社大学の問題です。例によって合っている保証なしです。
-----
m, n は自然数とする ( m > n )。「m と n が互いに素」⇔「2m - 1 と 2n - 1 が互いに素」を示せ ( 同志社 )
2m - 1 と 2n - 1 の差分は以下のように計算できます。
( 2m - 1 ) - ( 2n - 1 )
= 2m - 2n
= 2n[ 2m-n - 1 ]
m, n は互いに素であることから m - n は m, n の因数を持たず ( もし持つならば、m の因数を G、m = Gm'、m - n = GK としたとき m - n = Gm' - n = GK より n = G( m' - K ) となり m, n は共通の因数を持つので矛盾 )、m, n, m - n はそれぞれ互いに素になります。
m > n, m > m - n より、n と m - n に対して同様の操作を行うと、n > m - n の場合、 n, m - n, n - ( m - n ) = 2n - m は互いに素であり、n > m - n, n > 2n - m です。さらに m - n, 2n - m に対してこの操作を行います。以下、最大数 ( 最初は m ) を除いた 2 数でこの操作を繰り返すと、常に値は小さくなっていき最終的には差が 1 になります。この 2 数を M, N ( M > N )とすると M - N = 1 で
( 2M - 1 ) - ( 2N - 1 )
= 2M - 2N
= 2N[ 2M-N - 1 ] = 2N
であり、2M - 1 と 2N - 1 は奇数なので 2 を因数として持たず、従って互いに素です。遡って M + N, M, N では
( 2M+N - 1 ) - ( 2M - 1 ) = 2M( 2N - 1 )
より
2M+N - 1 = 2M( 2N - 1 ) + ( 2M - 1 )
であり、2M - 1 と 2N - 1 は互いに素で 2M は偶数なので 2M - 1 と 2M( 2N - 1 ) は互いに素なので、2M+N - 1, 2M - 1, 2N - 1 は それぞれ互いに素です。これを繰り返していくと最終的に 2m - 1 と 2n - 1 は互いに素になります。
ちなみに m = 7, n = 2 のとき
( 27 - 1 ) - ( 22 - 1 ) = 22( 25 - 1 ) [ 127 - 3 = 4・31 ) ]
( 25 - 1 ) - ( 22 - 1 ) = 22( 23 - 1 ) [ 31 - 3 = 4・7 ]
( 23 - 1 ) - ( 22 - 1 ) = 22 [ 7 - 3 = 4 ]
で 3, 7, 31, 127 は全て互いに素になります。
2m - 1, 2n - 1 はそれぞれ 1 のみからなる m, n 桁の二進数で表すことができます。m, n が互いに素でない時、m, n の共通因数を G とすると、2m - 1, 2n - 1 はどちらも 2G - 1 ( G 桁の 1 のみからなる二進数 ) で割り切れます。よって 2m - 1, 2n - 1 は共通因数 2G - 1 を持ち、互いに素ではありません。この対偶として、2m - 1, 2n - 1 が互いに素なら m, n は互いに素です。
2017年10月01日
読書の秋
10月になりました。今年も 100 日を切ったことになります。
読書の秋・スポーツの秋・食欲の秋などなど「何とかの秋」という言葉が多いですが、その由来は様々なようです。秋は読書をするのに最適な季節ということで「読書の秋」、実りの秋というように食べ物が豊富な季節ということで「食欲の秋」と呼ばれるようになったのだとか。
最近、読書の量が減ってきました。スマホを持つようになったのがきっかけでしょうか。またおもしろそうな本でも探して読もうかなと考えています。その前に、まだ読んでいない本を片付けなければなりませんが。
「数学問題bot(個人用)」から京大の問題です。例によって合っている保証なしです。
-----
a は正の実数とする。不等式 ax ≥ ax がすべての正の数 x に対して成り立つという。このとき a はどのようなものか ( 1993 京大後期 )
0 < a < 1 のときは ax → 0 ( x → +∞ ) に対して ax → +∞ ( x → +∞ ) なので明らかに成り立ちません。また、a = 1 のときは 左辺 1 に対して右辺は x → +∞ ( x → +∞ ) となるので、a > 1 のときだけを考えれば十分です。
ax ≥ ax の両辺に対して a を底とする対数をとると
x ≥ 1 + logax
となるので、x - logax - 1 ≥ 0 が任意の x で成り立てばよいことになります。そこで
f(x) = x - logax - 1
とすると
f'(x) = 1 - 1 / x・logea
なので、f'(x) = 0 のとき x = 1 / logea、x < 1 / logea で f'(x) < 0、x > 1 / logea で f'(x) > 0 となって f(x) は x = 1 / logea のとき極小値をとります。x = 1 / logea のとき
f(x) = 1 - loga( 1 / logea ) - 1 = - loga( 1 / logea )
なので、a > 1 より f(x) ≥ 0 が常に成り立つためには 1 / logea ≤ 1 であればよいことになります。同じく a > 1 より logea > 0 で、logea ≥ 1 より a ≥ e となります。
読書の秋・スポーツの秋・食欲の秋などなど「何とかの秋」という言葉が多いですが、その由来は様々なようです。秋は読書をするのに最適な季節ということで「読書の秋」、実りの秋というように食べ物が豊富な季節ということで「食欲の秋」と呼ばれるようになったのだとか。
最近、読書の量が減ってきました。スマホを持つようになったのがきっかけでしょうか。またおもしろそうな本でも探して読もうかなと考えています。その前に、まだ読んでいない本を片付けなければなりませんが。
「数学問題bot(個人用)」から京大の問題です。例によって合っている保証なしです。
-----
a は正の実数とする。不等式 ax ≥ ax がすべての正の数 x に対して成り立つという。このとき a はどのようなものか ( 1993 京大後期 )
0 < a < 1 のときは ax → 0 ( x → +∞ ) に対して ax → +∞ ( x → +∞ ) なので明らかに成り立ちません。また、a = 1 のときは 左辺 1 に対して右辺は x → +∞ ( x → +∞ ) となるので、a > 1 のときだけを考えれば十分です。
ax ≥ ax の両辺に対して a を底とする対数をとると
x ≥ 1 + logax
となるので、x - logax - 1 ≥ 0 が任意の x で成り立てばよいことになります。そこで
f(x) = x - logax - 1
とすると
f'(x) = 1 - 1 / x・logea
なので、f'(x) = 0 のとき x = 1 / logea、x < 1 / logea で f'(x) < 0、x > 1 / logea で f'(x) > 0 となって f(x) は x = 1 / logea のとき極小値をとります。x = 1 / logea のとき
f(x) = 1 - loga( 1 / logea ) - 1 = - loga( 1 / logea )
なので、a > 1 より f(x) ≥ 0 が常に成り立つためには 1 / logea ≤ 1 であればよいことになります。同じく a > 1 より logea > 0 で、logea ≥ 1 より a ≥ e となります。
2017年08月27日
とんちゃん
昨日は岐阜県の鵜沼にある「つたや」というところでとん焼を食べに行ってきました。個人的にはネギマがおいしかったです。
豚ホルモンというと名古屋人は「とんちゃん」を思い出します。味噌ダレに絡めた豚の腸の部位を焼いたもので、子供の頃からよく食べてました。今でも時々食べたくなる時があります。名古屋以外では「てっちゃん」というそうですね。
岐阜の「鶏ちゃん」はとんちゃんを鶏肉に変えたものでこちらの方が時代としては新しいと思っているのですが、本当のところはどうなんでしょう?鶏ちゃんもおいしいですよ。
「数学問題bot(個人用)」から京大の問題です。例によって合っている保証なしです。
-----
a, b, p, q は全て自然数で、( p2 + q2 ) / a = pq / b を満たしている。a と b は互いに素とする。√( a + 2b ) は自然数であることを示せ ( 1998 年京大後期文系 )
( p + q )2 = p2 + q2 + 2pq = ( a / b + 2 )pq = ( a + 2b )pq / b
より、a / b + 2 は a, b が互いに素であることから整数にはなれないので pq / b は整数、すなわち pq は b で割り切れることになります。
p, q の最大公約数を G、p = p'G, q = q'G とすると、
( p2 + q2 ) / a = G2( p'2 + q'2 ) / a
pq / b = G2p'q' / b
で、G ≠ 0 なので
( p'2 + q'2 ) / a = p'q' / b
で、p', q' は互いに素となります。
p' が持つ素因数は q' には存在せず、その逆も真なので、p'2 + q'2 は p', q' の素因数を持たず、従って p'2 + q'2 と p'q' は互いに素です。a, b が互いに素であることから G の中の素因数を a, b が共通で持つことはないので、
G2( p'2 + q'2 ) / a = G2p'q' / b
が成り立つためには
p'2 + q'2 = a
p'q' = b
でなければならず、従って pq / b = G2 となります。
( p + q )2 = ( a + 2b )G2
より、右辺が平方数になるためには a + 2b も平方数でなければならず、よって、 √( a + 2b ) は自然数になります。
豚ホルモンというと名古屋人は「とんちゃん」を思い出します。味噌ダレに絡めた豚の腸の部位を焼いたもので、子供の頃からよく食べてました。今でも時々食べたくなる時があります。名古屋以外では「てっちゃん」というそうですね。
岐阜の「鶏ちゃん」はとんちゃんを鶏肉に変えたものでこちらの方が時代としては新しいと思っているのですが、本当のところはどうなんでしょう?鶏ちゃんもおいしいですよ。
「数学問題bot(個人用)」から京大の問題です。例によって合っている保証なしです。
-----
a, b, p, q は全て自然数で、( p2 + q2 ) / a = pq / b を満たしている。a と b は互いに素とする。√( a + 2b ) は自然数であることを示せ ( 1998 年京大後期文系 )
( p + q )2 = p2 + q2 + 2pq = ( a / b + 2 )pq = ( a + 2b )pq / b
より、a / b + 2 は a, b が互いに素であることから整数にはなれないので pq / b は整数、すなわち pq は b で割り切れることになります。
p, q の最大公約数を G、p = p'G, q = q'G とすると、
( p2 + q2 ) / a = G2( p'2 + q'2 ) / a
pq / b = G2p'q' / b
で、G ≠ 0 なので
( p'2 + q'2 ) / a = p'q' / b
で、p', q' は互いに素となります。
p' が持つ素因数は q' には存在せず、その逆も真なので、p'2 + q'2 は p', q' の素因数を持たず、従って p'2 + q'2 と p'q' は互いに素です。a, b が互いに素であることから G の中の素因数を a, b が共通で持つことはないので、
G2( p'2 + q'2 ) / a = G2p'q' / b
が成り立つためには
p'2 + q'2 = a
p'q' = b
でなければならず、従って pq / b = G2 となります。
( p + q )2 = ( a + 2b )G2
より、右辺が平方数になるためには a + 2b も平方数でなければならず、よって、 √( a + 2b ) は自然数になります。
2017年08月13日
サンルイス
昨日はちょっとした飲み会があって出掛けていました。
サンルイスという南米料理が主体の店ですが、なぜか焼酎をボトルで頼むという普通の居酒屋と同じことをしていました。エビのガーリックオイル煮、おいしかったです。
「数学問題bot(個人用)」からこんな問題をチョイス。
-----
p, q は異なる自然数とする。また a を正の定数(自然数)とする。1/p, 1/a, 1/q がこの順に等差数列になることはあるか ( 2013 年京大 OP )
等差数列になるには 1/a - 1/p = 1/q - 1/a となる必要があります。この式を変形すると
1/p + 1/q = 2/a より a( p + q ) = 2pq
となります。p, q の最大公約数を G とし、p = p'G, q = q'G とすると、aG( p' + q' ) = 2p'q'G2 G ≠ 0 より
a( p' + q' ) = 2p'q'G
です。p', q' は互いに素なので、p', q' のどの素因数とも p' + q' は割り切れません。従って、a は p'q' で割り切れなくてはなりません。a に対してそのような数を見つけ、G を掛ければ目的の p, q を生成することができます。
ここで、右辺は 2 を係数として持つので、左辺は偶数です。a が奇数の場合は p', q' はどちらも奇数となるので、p' + q' は偶数となり問題はありません。a が偶数の場合、a/2 から p', q' を生成しなければなりません。
例として、a = 100 のとき、a/2 = 50 なので p' = 5, q' = 2 とすると、
(左辺) = 100( 5 + 2 ) = 700
(右辺) = 2・5・2G = 20G
より G = 35 になり、p = 175, q = 70 と求められます。このとき、
1 / 100 - 1 / 175 = ( 7 - 4 ) / 700 = 3 / 700
1 / 70 - 1 / 100 = ( 10 - 7 ) / 700 = 3 / 700
となるので等差数列となっています。a が素数の場合、例えば a = 7 のとき、p' = 7, q' = 1 とすれば
(左辺) = 7( 7 + 1 ) = 56
(右辺) = 2・7・1G = 14G
より G = 4 になり、p = 28, q = 4 とすれば、
1 / 7 - 1 / 28 = ( 4 - 1 ) / 28 = 3 / 28
1 / 4 - 1 / 7 = ( 7 - 4 ) / 28 = 3 / 28
で等差数列となります。
サンルイスという南米料理が主体の店ですが、なぜか焼酎をボトルで頼むという普通の居酒屋と同じことをしていました。エビのガーリックオイル煮、おいしかったです。
「数学問題bot(個人用)」からこんな問題をチョイス。
-----
p, q は異なる自然数とする。また a を正の定数(自然数)とする。1/p, 1/a, 1/q がこの順に等差数列になることはあるか ( 2013 年京大 OP )
等差数列になるには 1/a - 1/p = 1/q - 1/a となる必要があります。この式を変形すると
1/p + 1/q = 2/a より a( p + q ) = 2pq
となります。p, q の最大公約数を G とし、p = p'G, q = q'G とすると、aG( p' + q' ) = 2p'q'G2 G ≠ 0 より
a( p' + q' ) = 2p'q'G
です。p', q' は互いに素なので、p', q' のどの素因数とも p' + q' は割り切れません。従って、a は p'q' で割り切れなくてはなりません。a に対してそのような数を見つけ、G を掛ければ目的の p, q を生成することができます。
ここで、右辺は 2 を係数として持つので、左辺は偶数です。a が奇数の場合は p', q' はどちらも奇数となるので、p' + q' は偶数となり問題はありません。a が偶数の場合、a/2 から p', q' を生成しなければなりません。
例として、a = 100 のとき、a/2 = 50 なので p' = 5, q' = 2 とすると、
(左辺) = 100( 5 + 2 ) = 700
(右辺) = 2・5・2G = 20G
より G = 35 になり、p = 175, q = 70 と求められます。このとき、
1 / 100 - 1 / 175 = ( 7 - 4 ) / 700 = 3 / 700
1 / 70 - 1 / 100 = ( 10 - 7 ) / 700 = 3 / 700
となるので等差数列となっています。a が素数の場合、例えば a = 7 のとき、p' = 7, q' = 1 とすれば
(左辺) = 7( 7 + 1 ) = 56
(右辺) = 2・7・1G = 14G
より G = 4 になり、p = 28, q = 4 とすれば、
1 / 7 - 1 / 28 = ( 4 - 1 ) / 28 = 3 / 28
1 / 4 - 1 / 7 = ( 7 - 4 ) / 28 = 3 / 28
で等差数列となります。
2017年07月30日
魚料理
昨日はとある子ども向けのイベントに参加してきました。
夕食は子どもたちといっしょに食べたんですけど、そこにあった鯖の味噌煮にだれも手を出さなかったのにはちょっと笑いました。子どもには人気ないんですね。自分は好きなので食べましたが。
子どもたちにとっては魚よりも肉のほうが好きなんでしょうね。自分も子供の頃はそうでした。特に刺身が苦手でした。でも、三重県の鳥羽で捕れたての魚の刺身を食べたときはあまりのおいしさにビックリしました。それから少しずつ食べられるようになったような気が。
魚料理の中でも鯖の味噌煮というのは子どもにとっては地味に見えるんでしょう。もう少し見た目の派手なマリネとかならよかったのかも。
数学問題bot(個人用)から京大の問題です。例によって合っている保証はありません。
-----
a, b は a > b を満たす自然数とし、p, d は素数で p は奇素数とする。このとき、ap - bp = d であるならば、d を 2p で割った余りは 1 であることを示せ ( 95 京大前期 )
ap - bp = ( a - b )( ap-1 + ap-2b + ... + bp-1 ) より、d が素数ならば ap-1 + ap-2b + ... + bp-1 ≠ 1 より a - b = 1 である必要があります。従って、a = b + 1 であり、
d = ( b + 1 )p - bp
= Σk{0→p}( [ p! / k!(p-k)! ]bp-k ) - bp
= Σk{1→p-1}( [ p! / k!(p-k)! ]bp-k ) + 1
と変形することができます。ここで p は素数なので、p! / k!(p-k)! は分母の k!(p-k)! に含まれる素因数がすべて p と互いに素であり、p を和の外側にくくり出すことができます。従って、p をくくり出した後の和の部分を N として
d = pN + 1
の形に表すことができます。
d = ( b + 1 )p - bp より ( b + 1 )p と bp のいずれかが奇数なので d は奇数です。p は奇数なので、上式において N は偶数であることを意味し、N = 2M として
d = 2pM + 1
となります。よって、d は 2p で割ると 1 余ることが証明されました。
夕食は子どもたちといっしょに食べたんですけど、そこにあった鯖の味噌煮にだれも手を出さなかったのにはちょっと笑いました。子どもには人気ないんですね。自分は好きなので食べましたが。
子どもたちにとっては魚よりも肉のほうが好きなんでしょうね。自分も子供の頃はそうでした。特に刺身が苦手でした。でも、三重県の鳥羽で捕れたての魚の刺身を食べたときはあまりのおいしさにビックリしました。それから少しずつ食べられるようになったような気が。
魚料理の中でも鯖の味噌煮というのは子どもにとっては地味に見えるんでしょう。もう少し見た目の派手なマリネとかならよかったのかも。
数学問題bot(個人用)から京大の問題です。例によって合っている保証はありません。
-----
a, b は a > b を満たす自然数とし、p, d は素数で p は奇素数とする。このとき、ap - bp = d であるならば、d を 2p で割った余りは 1 であることを示せ ( 95 京大前期 )
ap - bp = ( a - b )( ap-1 + ap-2b + ... + bp-1 ) より、d が素数ならば ap-1 + ap-2b + ... + bp-1 ≠ 1 より a - b = 1 である必要があります。従って、a = b + 1 であり、
d = ( b + 1 )p - bp
= Σk{0→p}( [ p! / k!(p-k)! ]bp-k ) - bp
= Σk{1→p-1}( [ p! / k!(p-k)! ]bp-k ) + 1
と変形することができます。ここで p は素数なので、p! / k!(p-k)! は分母の k!(p-k)! に含まれる素因数がすべて p と互いに素であり、p を和の外側にくくり出すことができます。従って、p をくくり出した後の和の部分を N として
d = pN + 1
の形に表すことができます。
d = ( b + 1 )p - bp より ( b + 1 )p と bp のいずれかが奇数なので d は奇数です。p は奇数なので、上式において N は偶数であることを意味し、N = 2M として
d = 2pM + 1
となります。よって、d は 2p で割ると 1 余ることが証明されました。
2017年07月02日
今年も半分終わりました
早いもので、もう今年も半分が終わりました。
まだ梅雨も終わっていないのにやたらと暑い日が続きます。暑いだけならいいですが、湿度も高いので非常につらいですね。
今日も大雨でした。すぐには止みましたが、とても梅雨とは思えない豪雨でした。明日も雨なのでしょうか。憂うつです。
そういえば、蚊を 2 回も部屋の中で見つけました。いずれも退治し損ねました。あの羽音だけはどうにも我慢できません。しばらくはまた悩まされることになるんですね。
数学問題bot(個人用)からこんな問題を選んでみました。
-----
3 以上の任意の整数 n において、n < p < n! を満たす素数 p が少なくともひとつ存在することを示せ ( 1997 京都教育大 )
n = 3 のとき、3 < p < 3! = 6 を満たす素数 p として 5 があります。
n までの任意の整数に対して n < p < n! を満たす素数 p が少なくともひとつ存在すると仮定します。n + 1 に対して、n < n + 1 ≤ p < n! < ( n + 1 )! より p ≠ n + 1 ならば n + 1 < p < ( n + 1 )! を満たす素数 p が少なくともひとつ存在することになります。p = n + 1 のとき、素数 p に対して p < q < p! を満たす別の素数 q が少なくともひとつ存在することを証明すればいいことになります。
p! は 2 から p までのすべての数の積なので、特に p 以下のすべての素数で割り切れます。従って、 p! - 1 は p 以下のすべての素数に対して割り切ることができず、必ず -1 余ります。つまり、p! - 1 は p より大きな素数からなる積か、素数そのものであることになり、p < q < p! を満たす別の素数 q が少なくともひとつ存在することになります。よって、命題が成り立つことが証明されました。
まだ梅雨も終わっていないのにやたらと暑い日が続きます。暑いだけならいいですが、湿度も高いので非常につらいですね。
今日も大雨でした。すぐには止みましたが、とても梅雨とは思えない豪雨でした。明日も雨なのでしょうか。憂うつです。
そういえば、蚊を 2 回も部屋の中で見つけました。いずれも退治し損ねました。あの羽音だけはどうにも我慢できません。しばらくはまた悩まされることになるんですね。
数学問題bot(個人用)からこんな問題を選んでみました。
-----
3 以上の任意の整数 n において、n < p < n! を満たす素数 p が少なくともひとつ存在することを示せ ( 1997 京都教育大 )
n = 3 のとき、3 < p < 3! = 6 を満たす素数 p として 5 があります。
n までの任意の整数に対して n < p < n! を満たす素数 p が少なくともひとつ存在すると仮定します。n + 1 に対して、n < n + 1 ≤ p < n! < ( n + 1 )! より p ≠ n + 1 ならば n + 1 < p < ( n + 1 )! を満たす素数 p が少なくともひとつ存在することになります。p = n + 1 のとき、素数 p に対して p < q < p! を満たす別の素数 q が少なくともひとつ存在することを証明すればいいことになります。
p! は 2 から p までのすべての数の積なので、特に p 以下のすべての素数で割り切れます。従って、 p! - 1 は p 以下のすべての素数に対して割り切ることができず、必ず -1 余ります。つまり、p! - 1 は p より大きな素数からなる積か、素数そのものであることになり、p < q < p! を満たす別の素数 q が少なくともひとつ存在することになります。よって、命題が成り立つことが証明されました。
2017年06月04日
6 月に突入
6 月に入りました。
このところ、少し涼しい日が続いています。というよりその前の暑さが異常なのかもしれません。このまま梅雨に入るのでしょうかね。今度はゲリラ豪雨が心配です。
「数学問題bot」から久々に問題を解いてみました。もっとエレガントな解法があると思いますが、力づくで解いてます。例によって合っている保証はありません。
-----
4 桁の整数で,その下 2 桁の数と上 2 桁の数との和の平方と等しくなるものを求めよ ( 78 群馬大 )
上 2 桁を x ( 10 ≤ x < 100 )、下 2 桁を y ( 0 ≤ x < 100 ) とすると、
( x + y )2 = 100x + y
が成り立てばいいので、上式を x について解くと
x = -( y - 50 ) ± ( 2500 - 99y )1/2
となります。2 項目の根号内はゼロ以上でなければならないので、 0 ≤ y ≤ 25 という制限が追加されます。また、2 項目は整数でもなければならないので、根号内の数 2500 - 99y は平方数でもなければなりません。
2500 - 99y = 100( 25 - y ) + y
なので、y を 0 から 25 まで変化させて得られる数は上 2 桁が 25 - y、下 2 桁が y で表される 26 個の数となります。これを一つずつ平方数か調べていくわけですが、ここで次の手法を使います。
(1) 2 で割れて 4 で割れなければ平方数ではないので除外。4 で割れる場合、4 で割ってさらに 2 で割れるが 4 では割れなければやはり除外。
(2) 5 で割れて 25 で割れなければ平方数ではないので除外。
これに該当しない数は平方数であるかどうかを直接チェックします。
2500 = 502
2401 = 492
2302 (1) に該当 ×
2203 462 = 2116 と 472 = 2209 の間なので×
2104 (1) に該当 ×
2005 (2) に該当 ×
1906 (1) に該当 ×
1807 412 = 1681 と 422 = 1849 の間なので×
1708 4 で割って 427。 212 = 421 と 222 = 484 の間なので×
1609 402 = 1600 と 412 = 1681 の間なので×
1510 (1) に該当 ×
1411 372 = 1369 と 382 = 1444 の間なので×
1312 4 で 2 回割れて 82。92 = 81 と 102 = 100 の間なので×
1213 342 = 1156 と 352 = 1225 の間なので×
1114 (1) に該当 ×
1015 (2) に該当 ×
916 4 で割って 229。152 = 225 と 162 = 256 の間なので×
817 282 = 784 と 292 = 844 の間なので×
718 (1) に該当 ×
619 242 = 576 と 252 = 625 の間なので×
520 4 で割って 130。112 = 121 と 122 = 144 の間なので×
421 202 = 400 と 212 = 441 の間なので×
322 (1) に該当 ×
223 142 = 196 と 152 = 225 の間なので×
124 4 で割って 31。52 = 25 と 62 = 36 の間なので×
25 = 52
従って、y の候補としては 25, 1, 0 の三つあります。
y = 25 のとき x = 25 ± 5 = 30, 20 なので、3025, 2025 が条件を満たす数となります。y = 1 のとき x = 49 ± 49 = 98, 0 なので、9801 が条件を満たす数となります。最後の y = 0 のときは x = 50 ± 50 = 100, 0 なので、条件を満たす数はありません。
よって、条件を満たす数は 2025, 3025, 9801 の三つとなります。
このところ、少し涼しい日が続いています。というよりその前の暑さが異常なのかもしれません。このまま梅雨に入るのでしょうかね。今度はゲリラ豪雨が心配です。
「数学問題bot」から久々に問題を解いてみました。もっとエレガントな解法があると思いますが、力づくで解いてます。例によって合っている保証はありません。
-----
4 桁の整数で,その下 2 桁の数と上 2 桁の数との和の平方と等しくなるものを求めよ ( 78 群馬大 )
上 2 桁を x ( 10 ≤ x < 100 )、下 2 桁を y ( 0 ≤ x < 100 ) とすると、
( x + y )2 = 100x + y
が成り立てばいいので、上式を x について解くと
x = -( y - 50 ) ± ( 2500 - 99y )1/2
となります。2 項目の根号内はゼロ以上でなければならないので、 0 ≤ y ≤ 25 という制限が追加されます。また、2 項目は整数でもなければならないので、根号内の数 2500 - 99y は平方数でもなければなりません。
2500 - 99y = 100( 25 - y ) + y
なので、y を 0 から 25 まで変化させて得られる数は上 2 桁が 25 - y、下 2 桁が y で表される 26 個の数となります。これを一つずつ平方数か調べていくわけですが、ここで次の手法を使います。
(1) 2 で割れて 4 で割れなければ平方数ではないので除外。4 で割れる場合、4 で割ってさらに 2 で割れるが 4 では割れなければやはり除外。
(2) 5 で割れて 25 で割れなければ平方数ではないので除外。
これに該当しない数は平方数であるかどうかを直接チェックします。
2500 = 502
2401 = 492
2302 (1) に該当 ×
2203 462 = 2116 と 472 = 2209 の間なので×
2104 (1) に該当 ×
2005 (2) に該当 ×
1906 (1) に該当 ×
1807 412 = 1681 と 422 = 1849 の間なので×
1708 4 で割って 427。 212 = 421 と 222 = 484 の間なので×
1609 402 = 1600 と 412 = 1681 の間なので×
1510 (1) に該当 ×
1411 372 = 1369 と 382 = 1444 の間なので×
1312 4 で 2 回割れて 82。92 = 81 と 102 = 100 の間なので×
1213 342 = 1156 と 352 = 1225 の間なので×
1114 (1) に該当 ×
1015 (2) に該当 ×
916 4 で割って 229。152 = 225 と 162 = 256 の間なので×
817 282 = 784 と 292 = 844 の間なので×
718 (1) に該当 ×
619 242 = 576 と 252 = 625 の間なので×
520 4 で割って 130。112 = 121 と 122 = 144 の間なので×
421 202 = 400 と 212 = 441 の間なので×
322 (1) に該当 ×
223 142 = 196 と 152 = 225 の間なので×
124 4 で割って 31。52 = 25 と 62 = 36 の間なので×
25 = 52
従って、y の候補としては 25, 1, 0 の三つあります。
y = 25 のとき x = 25 ± 5 = 30, 20 なので、3025, 2025 が条件を満たす数となります。y = 1 のとき x = 49 ± 49 = 98, 0 なので、9801 が条件を満たす数となります。最後の y = 0 のときは x = 50 ± 50 = 100, 0 なので、条件を満たす数はありません。
よって、条件を満たす数は 2025, 3025, 9801 の三つとなります。
2017年03月19日
名大入試問題 2017 (6)
明日は「春分の日」です。個人的にはもっと暖かくなってほしいところです。
2017 年名大入試問題のラストです。結構、悩まされました。
-----
次の問に答えよ。
(1) 次の条件 (*) を満たす 3 つの自然数の組 ( a, b, c ) をすべて求めよ。
(*) a < b < c かつ 1/a +1/b + 1/c = 1/2 である。
(2) 偶数 2n ( n ≥ 1 ) の 3 つの正の約数 p, q, r で p > q > r と p + q + r = n を満たす組 ( p, q, r ) の個数を f(n) とする。ただし、条件を満たす組が存在しない場合は、f(n) = 0 とする。n が自然数全体を動くときの f(n) の最大値 M を求めよ。また、f(n) = M となる自然数 n の中で最小のものを求めよ。
(1) (*) より 1/a > 1/2 なので a > 2 になります。
a = 3 のとき、1/b + 1/c = 1/2 - 1/3 = 1/6 より 1/b < 1/6 なので b > 6 です。
b = 7 のとき 1/c = 1/6 - 1/7 = 1/42、b = 8 のとき 1/c = 1/6 - 1/8 = 1/24、b = 9 のとき 1/c = 1/6 - 1/9 = 1/18、b = 10 のとき 1/c = 1/6 - 1/10 = 1/15、b = 11 のとき 1/c = 1/6 - 1/11 = 5/66、b = 12 のとき 1/c = 1/6 - 1/12 = 1/12 で b = c となるのでこれ以上はありません。よって、( 3, 7, 42 ), ( 3, 8, 24 ), ( 3, 9, 18 ), ( 3, 10, 15 ) が得られます。
a = 4 のとき、1/b + 1/c = 1/2 - 1/4 = 1/4 より 1/b < 1/4 なので b > 4 です。
b = 5 のとき 1/c = 1/4 - 1/5 = 1/20、b = 6 のとき 1/c = 1/4 - 1/6 = 1/12、b = 7 のとき 1/c = 1/4 - 1/7 = 3/28、b = 8 のとき 1/c = 1/4 - 1/8 = 1/8 で b = c となるのでこれ以上はありません。よって、( 4, 5, 20 ), ( 4, 6, 12 ) が得られます。
a = 5 のとき、1/b + 1/c = 1/2 - 1/5 = 3/10 より 1/b < 3/10 なので b > 3 ですが、a = 5 なので b ≥ 6 となります。
b = 6 のとき 1/c = 3/10 - 1/6 = 2/15、b = 7 のとき 1/c = 3/10 - 1/7 = 11/70 > 1/7 で b > c となるのでこれ以上はありません。
a = 6 のとき、1/b + 1/c = 1/2 - 1/6 = 1/3 より 1/b < 1/3 なので b > 3 ですが、a = 6 なので b ≥ 7 となります。
b = 7 のとき 1/c = 1/3 - 1/7 = 4/21 > 1/7 で b > c となるのでこれ以上はありません。
以下、a ≥ 6 のときは b ≥ a + 1 であり、1/c = 1/2 - 1/a - 1/(a+1) ≥ 1/2 - 1/6 - 1/7 = 4/21 > 1/7 より c < 7 となり、 a < b < c を満たさなくなるのでこれ以上はありません。
よって、( 3, 7, 42 ), ( 3, 8, 24 ), ( 3, 9, 18 ), ( 3, 10, 15 ), ( 4, 5, 20 ), ( 4, 6, 12 ) の 6 つになります。
(2) p = 2n/p'、q = 2n/q'、r = 2n/q' とすると、p' < q' < r' かつ 1/p' + 1/q' + 1/r' = p/2n + q/2n + r/2n = 1/2 となるので、( p', q', r' ) の組は (1) でもとめたものに限ります。以下、k を 1 以上の整数とします。
( p', q', r' ) = ( 3, 7, 42 ) のとき、n = 21k ならば p = 14k, q = 6k, r = k で p + q + r = 21k なので成り立ちます。
( p', q', r' ) = ( 3, 8, 24 ) のとき、n = 12k ならば p = 8k, q = 3k, r = k で p + q + r = 12k なので成り立ちます。
( p', q', r' ) = ( 3, 9, 18 ) のとき、n = 9k ならば p = 6k, q = 2k, r = k で p + q + r = 9k なので成り立ちます。
( p', q', r' ) = ( 3, 10, 15 ) のとき、n = 15k ならば p = 10k, q = 3k, r = 2k で p + q + r = 15k なので成り立ちます。
( p', q', r' ) = ( 4, 5, 20 ) のとき、n = 10k ならば p = 5k, q = 4k, r = k で p + q + r = 10k なので成り立ちます。
( p', q', r' ) = ( 4, 6, 12 ) のとき、n = 6k ならば p = 3k, q = 2k, r = k で p + q + r = 6k なので成り立ちます。
すなわち、n = 6k, 9k, 10k, 12k, 15k, 21k のとき p + q + r = n を満たす ( p, q, r ) の組が存在することになります。これらの最初公倍数は 2・2・3・3・5・7k = 1260k で、このとき f(n) = 6 となります。よって、M = 6 で、最小の数は 1260 です。
2017 年名大入試問題のラストです。結構、悩まされました。
-----
次の問に答えよ。
(1) 次の条件 (*) を満たす 3 つの自然数の組 ( a, b, c ) をすべて求めよ。
(*) a < b < c かつ 1/a +1/b + 1/c = 1/2 である。
(2) 偶数 2n ( n ≥ 1 ) の 3 つの正の約数 p, q, r で p > q > r と p + q + r = n を満たす組 ( p, q, r ) の個数を f(n) とする。ただし、条件を満たす組が存在しない場合は、f(n) = 0 とする。n が自然数全体を動くときの f(n) の最大値 M を求めよ。また、f(n) = M となる自然数 n の中で最小のものを求めよ。
(1) (*) より 1/a > 1/2 なので a > 2 になります。
a = 3 のとき、1/b + 1/c = 1/2 - 1/3 = 1/6 より 1/b < 1/6 なので b > 6 です。
b = 7 のとき 1/c = 1/6 - 1/7 = 1/42、b = 8 のとき 1/c = 1/6 - 1/8 = 1/24、b = 9 のとき 1/c = 1/6 - 1/9 = 1/18、b = 10 のとき 1/c = 1/6 - 1/10 = 1/15、b = 11 のとき 1/c = 1/6 - 1/11 = 5/66、b = 12 のとき 1/c = 1/6 - 1/12 = 1/12 で b = c となるのでこれ以上はありません。よって、( 3, 7, 42 ), ( 3, 8, 24 ), ( 3, 9, 18 ), ( 3, 10, 15 ) が得られます。
a = 4 のとき、1/b + 1/c = 1/2 - 1/4 = 1/4 より 1/b < 1/4 なので b > 4 です。
b = 5 のとき 1/c = 1/4 - 1/5 = 1/20、b = 6 のとき 1/c = 1/4 - 1/6 = 1/12、b = 7 のとき 1/c = 1/4 - 1/7 = 3/28、b = 8 のとき 1/c = 1/4 - 1/8 = 1/8 で b = c となるのでこれ以上はありません。よって、( 4, 5, 20 ), ( 4, 6, 12 ) が得られます。
a = 5 のとき、1/b + 1/c = 1/2 - 1/5 = 3/10 より 1/b < 3/10 なので b > 3 ですが、a = 5 なので b ≥ 6 となります。
b = 6 のとき 1/c = 3/10 - 1/6 = 2/15、b = 7 のとき 1/c = 3/10 - 1/7 = 11/70 > 1/7 で b > c となるのでこれ以上はありません。
a = 6 のとき、1/b + 1/c = 1/2 - 1/6 = 1/3 より 1/b < 1/3 なので b > 3 ですが、a = 6 なので b ≥ 7 となります。
b = 7 のとき 1/c = 1/3 - 1/7 = 4/21 > 1/7 で b > c となるのでこれ以上はありません。
以下、a ≥ 6 のときは b ≥ a + 1 であり、1/c = 1/2 - 1/a - 1/(a+1) ≥ 1/2 - 1/6 - 1/7 = 4/21 > 1/7 より c < 7 となり、 a < b < c を満たさなくなるのでこれ以上はありません。
よって、( 3, 7, 42 ), ( 3, 8, 24 ), ( 3, 9, 18 ), ( 3, 10, 15 ), ( 4, 5, 20 ), ( 4, 6, 12 ) の 6 つになります。
(2) p = 2n/p'、q = 2n/q'、r = 2n/q' とすると、p' < q' < r' かつ 1/p' + 1/q' + 1/r' = p/2n + q/2n + r/2n = 1/2 となるので、( p', q', r' ) の組は (1) でもとめたものに限ります。以下、k を 1 以上の整数とします。
( p', q', r' ) = ( 3, 7, 42 ) のとき、n = 21k ならば p = 14k, q = 6k, r = k で p + q + r = 21k なので成り立ちます。
( p', q', r' ) = ( 3, 8, 24 ) のとき、n = 12k ならば p = 8k, q = 3k, r = k で p + q + r = 12k なので成り立ちます。
( p', q', r' ) = ( 3, 9, 18 ) のとき、n = 9k ならば p = 6k, q = 2k, r = k で p + q + r = 9k なので成り立ちます。
( p', q', r' ) = ( 3, 10, 15 ) のとき、n = 15k ならば p = 10k, q = 3k, r = 2k で p + q + r = 15k なので成り立ちます。
( p', q', r' ) = ( 4, 5, 20 ) のとき、n = 10k ならば p = 5k, q = 4k, r = k で p + q + r = 10k なので成り立ちます。
( p', q', r' ) = ( 4, 6, 12 ) のとき、n = 6k ならば p = 3k, q = 2k, r = k で p + q + r = 6k なので成り立ちます。
すなわち、n = 6k, 9k, 10k, 12k, 15k, 21k のとき p + q + r = n を満たす ( p, q, r ) の組が存在することになります。これらの最初公倍数は 2・2・3・3・5・7k = 1260k で、このとき f(n) = 6 となります。よって、M = 6 で、最小の数は 1260 です。
2017年03月18日
名大入試問題 2017 (5)
歯医者で検診がありました。結果、虫歯が一本。治療が必要ということで憂うつです。
2017 年名大入試文系の問題です。去年と同様、全体的に文系のほうが難しいと感じました。
-----
a を正の定数とする。2 次関数 f(x) = ax2 と 3 次関数 g(x) x( x - 4 )2 について、次の問に答えよ。
(1) 関数 y = g(x) について、極値を求め、そのグラフを描け。
(2) 2 つの曲線 y = f(x) と y = g(x) は相異なる 3 点で交わることを示せ。
(3) 2 つの曲線 y = f(x) と y = g(x) で囲まれた 2 つの部分の面積が等しくなるように a の値を定めよ。またそのとき、2 つの曲線の交点の x 座標を求めよ。
(1) g(x) = x( x - 4 )2 より
g'(x) = ( x - 4 )2 + 2x( x - 4 )
= ( x - 4 )( 3x - 4 )
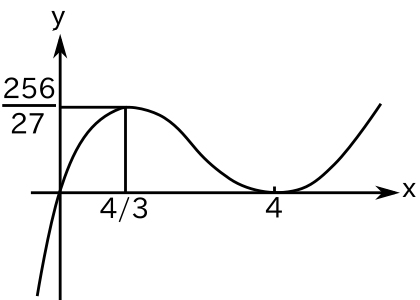
なので、x = 4, 4/3 のとき極値になります。g(4) = 0, g(4/3) = 256/27 で増減表は
なのでグラフは下図のようになります。
(2) f(x) = g(x) のとき、x( x - 4 )2 = ax2 より明らかに x = 0 を買いに持ちます。
x ≠ 0 のとき、両辺を x で割って ( x - 4 )2 = ax より
x2 - ( a + 8 )x + 16 = 0
の判別式 D を求めると
D = ( a + 8 )2 - 64 = a2 + 16a
となり、a は正の定数なので D > 0 より実数解は 2 つ存在します。従って、命題が成り立ちます。
(3) 2 つの解を r, s ( 但し r < s ) としたとき、
∫{0→s} x( x - 4 )2 - ax2 dx = 0
が成り立てばよいので、上式の左辺を計算すると
(左辺) = ∫{0→s} x3 - 8x2 + 16x - ax2 dx
= [ (1/4)x4 - (8/3)x3 + 8x2 - (a/3)x3 ]{0→s}
= (1/4)s4 - (8/3)s3 + 8s2 - (a/3)s3 = 0
となります。s ≠ 0 より左辺を s2 / 12 で割って
3s2 - ( 4a + 32 )s + 96 = 0
より a = (3/4)s + 24/s - 8 になります。r, s の値を計算すると
[ ( a + 8 ) ± ( a2 + 16a )1/2 ] / 2 で s は符号が + の方なので、
1/s = 2 / [ ( a + 8 ) ± ( a2 + 16a )1/2 ]
= [ ( a + 8 ) - ( a2 + 16a )1/2 ] / 32
より
a = (3/8)[ ( a + 8 ) + ( a2 + 16a )1/2 ] + (3/4)[ ( a + 8 ) - ( a2 + 16a )1/2 ] - 8
= (9/8)( a + 8 ) - (3/8)( a2 + 16a )1/2 - 8
となります。式を変形して
(1/8)a + 1 = (3/8)( a2 + 16a )1/2
より両辺に 8 を描けて 2 乗すると
( a + 8 )2 = 9( a2 + 16a )
式を整理して
a2 + 16a - 8 = 0
となります。従って
a = -8 ± 6√2
で a > 0 より a = -8 + 6√2 となります。このとき、r, s は
{ [ ( -8 + 6√2 ) + 8 ] ± [ ( -8 + 6√2 )2 + 16( -8 + 6√2 ) ]1/2 } / 2
= ( 6√2 ± √8 ) / 2 = 2√2, 4√2
と求められます。
2017 年名大入試文系の問題です。去年と同様、全体的に文系のほうが難しいと感じました。
-----
a を正の定数とする。2 次関数 f(x) = ax2 と 3 次関数 g(x) x( x - 4 )2 について、次の問に答えよ。
(1) 関数 y = g(x) について、極値を求め、そのグラフを描け。
(2) 2 つの曲線 y = f(x) と y = g(x) は相異なる 3 点で交わることを示せ。
(3) 2 つの曲線 y = f(x) と y = g(x) で囲まれた 2 つの部分の面積が等しくなるように a の値を定めよ。またそのとき、2 つの曲線の交点の x 座標を求めよ。
(1) g(x) = x( x - 4 )2 より
g'(x) = ( x - 4 )2 + 2x( x - 4 )
= ( x - 4 )( 3x - 4 )
なので、x = 4, 4/3 のとき極値になります。g(4) = 0, g(4/3) = 256/27 で増減表は
| x | 0 | 4/3 | 4 | ||||
|---|---|---|---|---|---|---|---|
| g(x) | - | 0 | + | 256/27 | + | 0 | - |
| g'(x) | + | 0 | - | 0 | + | ||
なのでグラフは下図のようになります。

(2) f(x) = g(x) のとき、x( x - 4 )2 = ax2 より明らかに x = 0 を買いに持ちます。
x ≠ 0 のとき、両辺を x で割って ( x - 4 )2 = ax より
x2 - ( a + 8 )x + 16 = 0
の判別式 D を求めると
D = ( a + 8 )2 - 64 = a2 + 16a
となり、a は正の定数なので D > 0 より実数解は 2 つ存在します。従って、命題が成り立ちます。
(3) 2 つの解を r, s ( 但し r < s ) としたとき、
∫{0→s} x( x - 4 )2 - ax2 dx = 0
が成り立てばよいので、上式の左辺を計算すると
(左辺) = ∫{0→s} x3 - 8x2 + 16x - ax2 dx
= [ (1/4)x4 - (8/3)x3 + 8x2 - (a/3)x3 ]{0→s}
= (1/4)s4 - (8/3)s3 + 8s2 - (a/3)s3 = 0
となります。s ≠ 0 より左辺を s2 / 12 で割って
3s2 - ( 4a + 32 )s + 96 = 0
より a = (3/4)s + 24/s - 8 になります。r, s の値を計算すると
[ ( a + 8 ) ± ( a2 + 16a )1/2 ] / 2 で s は符号が + の方なので、
1/s = 2 / [ ( a + 8 ) ± ( a2 + 16a )1/2 ]
= [ ( a + 8 ) - ( a2 + 16a )1/2 ] / 32
より
a = (3/8)[ ( a + 8 ) + ( a2 + 16a )1/2 ] + (3/4)[ ( a + 8 ) - ( a2 + 16a )1/2 ] - 8
= (9/8)( a + 8 ) - (3/8)( a2 + 16a )1/2 - 8
となります。式を変形して
(1/8)a + 1 = (3/8)( a2 + 16a )1/2
より両辺に 8 を描けて 2 乗すると
( a + 8 )2 = 9( a2 + 16a )
式を整理して
a2 + 16a - 8 = 0
となります。従って
a = -8 ± 6√2
で a > 0 より a = -8 + 6√2 となります。このとき、r, s は
{ [ ( -8 + 6√2 ) + 8 ] ± [ ( -8 + 6√2 )2 + 16( -8 + 6√2 ) ]1/2 } / 2
= ( 6√2 ± √8 ) / 2 = 2√2, 4√2
と求められます。
2017年03月12日
名大入試問題 2017 (4)
暑さ寒さも彼岸までとは言いますが、来週になれば暖かくなるのでしょうかね。
少し前に「ブラック・ジャック」の 1, 2 巻を買いました。昔の単行本のやつです。まだ買えるんですねこれ。
久しぶりに読みましたがやっぱり面白いです。続けてほしくなりましたが、コンプリートしようとすると結構お金かかるんですよね。どうしましょうか。
2017 年の名大入試問題の理系最後の問題です。次回から文系に移ります。
-----
n を自然数とする。0 でない複素数からなる集合 M が次の条件 (I), (II), (III) を満たしている。
(I) 集合 M は n 個の要素からなる。
(II) 集合 M の要素 z に対して 1 / z と -z はともに集合 M の要素である。
(III) 集合 M の要素 z, w に対して、その積 zw は集合 M の要素である。ただし、z = w の場合も含める。
このとき、次の問に答えよ。
(1) 1 および -1 は集合 M の要素であることを示せ。
(2) n は偶数であることを示せ。
(3) n = 4 のとき、集合 M は一通りに定まることを示し、その要素をすべて求めよ。
(3) n = 6 のとき、集合 M は一通りに定まることを示し、その要素をすべて求めよ。
(1) 集合 M のある要素 z に対して (II) より 1 / z は M の要素なので、(III) より z と 1 / z の積 1 は必ず集合 M の要素となります。また、(II) より -z も M の要素なので、(III) より -z と 1 / z の積 -1 も M の要素です。
(2) (1) より { 1, -1 } は必ず集合 M の要素となるので、M の一つの要素を z としたとき -1 との積 -z が必ず M に存在します。0 を含まないことから z ≠ -z かつ集合 M の異なる二つの要素 z1, z2 に対して -z1 ≠ -z2 なので、集合 M の要素は { z, -z } のペアをちょうど複数個持つことになり、n は偶数となります。
(3) { 1, -1 } は必ず M にあるので、残り 2 つの要素は ±1 とは異なるある複素数 z に対して [ z, 1 / z, -z } で表され、z ≠ -z より 1 / z は z, -z のいずれかと等しいことになります。z = 1 / z のとき z2 = 1 より z = ±1 なので条件を満たしません。-z = 1 / z のとき z2 = -1 となり、z = i より 4 つの要素 { 1, -1, i, -i } が決まります。
(4) ±1 とは異なるある複素数 z に対して条件 (III) より z2 も M の要素となります。z2 = 1 のとき z = ±1 であり条件を満たしません。また、z2 = -1 のとき z = i なので、これは n = 4 の場合に該当します。z2 = ±z のとき z = ±1 なのでこれらも除外すると、z2 は新たな要素であることになります。従って、{ 1, -1, z, -z, z2, -z2 } は集合 M の要素の一部を表し、その他に ±1 / z, ±1 / z2 も集合 M に含まれます。
1 / z = ±z のときは z2 = ±1 となりこれは n = 2, 4 の場合に該当します。
1 / z = z2 のとき z3 = 1 より 1 以外の解は z = ( -1 ± √3i ) / 2 となります。このとき、1 / z = 2 / ( -1 ± √3i ) = ( -1 ∓√3i ) / 2 = z2 であり、1 / z2 = 2 / ( -1 ∓√3i ) = ( -1 ±√3i ) / 2 = z となります。
1 / z = -z2 のとき z3 = -1 より -1 以外の解は z = ( 1 ± √3i ) / 2 となります。このとき、1 / z = 2 / ( 1 ± √3i ) = ( 1 ∓√3i ) / 2 = z2 であり、1 / z2 = 2 / ( 1 ∓√3i ) = ( 1 ±√3i ) / 2 = z となります。
よって、n = 6 のときは { 1, -1, ( 1 ± √3i ) / 2, ( -1 ± √3i ) / 2 } のみとなります。
少し前に「ブラック・ジャック」の 1, 2 巻を買いました。昔の単行本のやつです。まだ買えるんですねこれ。
久しぶりに読みましたがやっぱり面白いです。続けてほしくなりましたが、コンプリートしようとすると結構お金かかるんですよね。どうしましょうか。
2017 年の名大入試問題の理系最後の問題です。次回から文系に移ります。
-----
n を自然数とする。0 でない複素数からなる集合 M が次の条件 (I), (II), (III) を満たしている。
(I) 集合 M は n 個の要素からなる。
(II) 集合 M の要素 z に対して 1 / z と -z はともに集合 M の要素である。
(III) 集合 M の要素 z, w に対して、その積 zw は集合 M の要素である。ただし、z = w の場合も含める。
このとき、次の問に答えよ。
(1) 1 および -1 は集合 M の要素であることを示せ。
(2) n は偶数であることを示せ。
(3) n = 4 のとき、集合 M は一通りに定まることを示し、その要素をすべて求めよ。
(3) n = 6 のとき、集合 M は一通りに定まることを示し、その要素をすべて求めよ。
(1) 集合 M のある要素 z に対して (II) より 1 / z は M の要素なので、(III) より z と 1 / z の積 1 は必ず集合 M の要素となります。また、(II) より -z も M の要素なので、(III) より -z と 1 / z の積 -1 も M の要素です。
(2) (1) より { 1, -1 } は必ず集合 M の要素となるので、M の一つの要素を z としたとき -1 との積 -z が必ず M に存在します。0 を含まないことから z ≠ -z かつ集合 M の異なる二つの要素 z1, z2 に対して -z1 ≠ -z2 なので、集合 M の要素は { z, -z } のペアをちょうど複数個持つことになり、n は偶数となります。
(3) { 1, -1 } は必ず M にあるので、残り 2 つの要素は ±1 とは異なるある複素数 z に対して [ z, 1 / z, -z } で表され、z ≠ -z より 1 / z は z, -z のいずれかと等しいことになります。z = 1 / z のとき z2 = 1 より z = ±1 なので条件を満たしません。-z = 1 / z のとき z2 = -1 となり、z = i より 4 つの要素 { 1, -1, i, -i } が決まります。
(4) ±1 とは異なるある複素数 z に対して条件 (III) より z2 も M の要素となります。z2 = 1 のとき z = ±1 であり条件を満たしません。また、z2 = -1 のとき z = i なので、これは n = 4 の場合に該当します。z2 = ±z のとき z = ±1 なのでこれらも除外すると、z2 は新たな要素であることになります。従って、{ 1, -1, z, -z, z2, -z2 } は集合 M の要素の一部を表し、その他に ±1 / z, ±1 / z2 も集合 M に含まれます。
1 / z = ±z のときは z2 = ±1 となりこれは n = 2, 4 の場合に該当します。
1 / z = z2 のとき z3 = 1 より 1 以外の解は z = ( -1 ± √3i ) / 2 となります。このとき、1 / z = 2 / ( -1 ± √3i ) = ( -1 ∓√3i ) / 2 = z2 であり、1 / z2 = 2 / ( -1 ∓√3i ) = ( -1 ±√3i ) / 2 = z となります。
1 / z = -z2 のとき z3 = -1 より -1 以外の解は z = ( 1 ± √3i ) / 2 となります。このとき、1 / z = 2 / ( 1 ± √3i ) = ( 1 ∓√3i ) / 2 = z2 であり、1 / z2 = 2 / ( 1 ∓√3i ) = ( 1 ±√3i ) / 2 = z となります。
よって、n = 6 のときは { 1, -1, ( 1 ± √3i ) / 2, ( -1 ± √3i ) / 2 } のみとなります。
2017年03月11日
名大入試問題 2017 (3)
今日は 3 月 11 日です。
Yahoo で「3.11」と検索すると、10 円が寄付されます。但し、3 月 11 日中だけです。今なら間に合いますよ。
2017 年名大入試問題の 3 問目です。そういえば、合格発表がすでにあったようですね。
-----
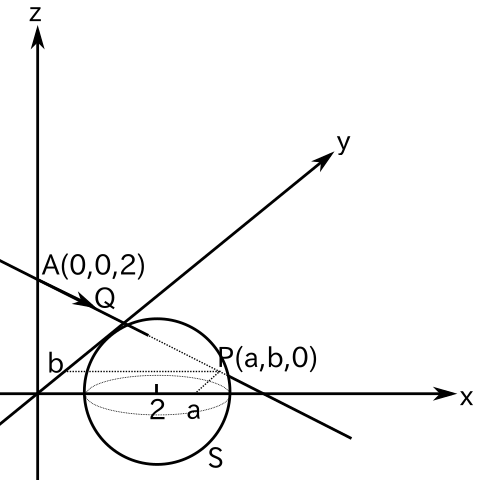
xyz 空間の 2 点 A( 0, 0, 2 ), P( a, b, 0 ) を通る直線を l とする。また、点 ( 2, 0, 0 ) を中心都市、半径が √2 である球面を S で表し、S のうち z 座標が z > 0 を満たす部分を T とする。このとき、次の問に答えよ。
(1) l 上に点 Q がある。実数 t を [AQ] = t[AP] ( [XY]は二点 X, Y を結ぶベクトルを表す ) で定めるとき、点 Q の座標を a, b, t を使って表せ。
(2) l が S と相異なる 2 点で交わるような実数 a, b に関する条件を求め、ab 平面上に図示せよ。
(3) l が T と相異なる 2 点で交わるような実数 a, b に関する条件を求め、ab 平面上に図示せよ。
(1) 図より Q( at, bt, 2 - 2t ) です。
(2) l と S の交点を Q とすると、( at - 2 )2 + ( bt )2 + ( 2 - 2t )2 = 2 が成り立ちます。これを変形すると
( a2 + b2 + 4 )t2 - ( 4a + 8 )t + 6 = 0
これが異なる実数解を持つためには判別式 D > 0 である必要があります。従って
D = ( 4a + 8 )2 - 24( a2 + b2 + 4 )
= -8a2 + 64a - 24b2 - 32 > 0 より
a2 - 8a + 3b2 + 4 < 0
( a - 4 )2 + 3b2 < 12 が条件となります。
(3) P が球の内部にある場合、l は T 上の 1 点と、S の z ≤ 0 の領域の 1 点で交差することになります。従ってこの範囲では成り立たず、( a - 2 )2 + b2 > 2 でなければなりません。
P が球の外部にある場合、S の z > 0 の領域の 2 点で交差する場合が成り立つ範囲となります。f(t) = ( a2 + b2 + 4 )t2 - ( 4a + 8 )t + 6 としたとき、|AQ| < |AP| となることからこの関数は t < 1 の領域で実数解を持つので
(i) f(1) > 0
(ii) f'(1) > 0
の二つが成り立つことになります。(i) より
f(1) = ( a2 + b2 + 4 ) - ( 4a + 8 ) + 6 = ( a - 2 )2 + b2 - 2 > 0
なのでこれは先程求めた範囲に等しくなります。また、(ii) より
f'(1) = 2( a2 + b2 + 4 ) - ( 4a + 8 ) = 2( a - 1 )2 + 2b2 - 2 > 0
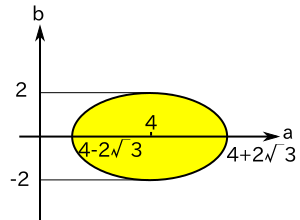
なので、( a - 1 )2 + b2 > 1 がもう一つの範囲となります。(2) の結果と合わせると、求める条件は
( a - 4 )2 + 3b2 < 12
( a - 2 )2 + b2 > 2
( a - 1 )2 + b2 > 1
となります。
( a - 4 )2 + 3b2 = 12 と ( a - 2 )2 + b2 = 2 の交点は ( a, b ) = ( 1, ±1 ) です。
また、( a - 2 )2 + b2 = 2 と ( a - 1 )2 + b2 = 1 の交点も ( a, b ) = ( 1, ±1 ) で、この 3 つの曲線は同じ点 ( a, b ) = ( 1, ±1 ) で交わります。それに注意して図示すると以下のようになります。
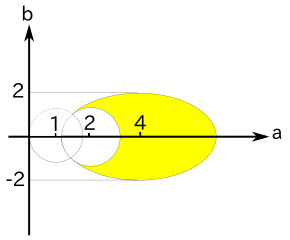
Yahoo で「3.11」と検索すると、10 円が寄付されます。但し、3 月 11 日中だけです。今なら間に合いますよ。
2017 年名大入試問題の 3 問目です。そういえば、合格発表がすでにあったようですね。
-----
xyz 空間の 2 点 A( 0, 0, 2 ), P( a, b, 0 ) を通る直線を l とする。また、点 ( 2, 0, 0 ) を中心都市、半径が √2 である球面を S で表し、S のうち z 座標が z > 0 を満たす部分を T とする。このとき、次の問に答えよ。
(1) l 上に点 Q がある。実数 t を [AQ] = t[AP] ( [XY]は二点 X, Y を結ぶベクトルを表す ) で定めるとき、点 Q の座標を a, b, t を使って表せ。
(2) l が S と相異なる 2 点で交わるような実数 a, b に関する条件を求め、ab 平面上に図示せよ。
(3) l が T と相異なる 2 点で交わるような実数 a, b に関する条件を求め、ab 平面上に図示せよ。
(1) 図より Q( at, bt, 2 - 2t ) です。

(2) l と S の交点を Q とすると、( at - 2 )2 + ( bt )2 + ( 2 - 2t )2 = 2 が成り立ちます。これを変形すると
( a2 + b2 + 4 )t2 - ( 4a + 8 )t + 6 = 0
これが異なる実数解を持つためには判別式 D > 0 である必要があります。従って
D = ( 4a + 8 )2 - 24( a2 + b2 + 4 )
= -8a2 + 64a - 24b2 - 32 > 0 より
a2 - 8a + 3b2 + 4 < 0
( a - 4 )2 + 3b2 < 12 が条件となります。

(3) P が球の内部にある場合、l は T 上の 1 点と、S の z ≤ 0 の領域の 1 点で交差することになります。従ってこの範囲では成り立たず、( a - 2 )2 + b2 > 2 でなければなりません。
P が球の外部にある場合、S の z > 0 の領域の 2 点で交差する場合が成り立つ範囲となります。f(t) = ( a2 + b2 + 4 )t2 - ( 4a + 8 )t + 6 としたとき、|AQ| < |AP| となることからこの関数は t < 1 の領域で実数解を持つので

(i) f(1) > 0
(ii) f'(1) > 0
の二つが成り立つことになります。(i) より
f(1) = ( a2 + b2 + 4 ) - ( 4a + 8 ) + 6 = ( a - 2 )2 + b2 - 2 > 0
なのでこれは先程求めた範囲に等しくなります。また、(ii) より
f'(1) = 2( a2 + b2 + 4 ) - ( 4a + 8 ) = 2( a - 1 )2 + 2b2 - 2 > 0
なので、( a - 1 )2 + b2 > 1 がもう一つの範囲となります。(2) の結果と合わせると、求める条件は
( a - 4 )2 + 3b2 < 12
( a - 2 )2 + b2 > 2
( a - 1 )2 + b2 > 1
となります。
( a - 4 )2 + 3b2 = 12 と ( a - 2 )2 + b2 = 2 の交点は ( a, b ) = ( 1, ±1 ) です。
また、( a - 2 )2 + b2 = 2 と ( a - 1 )2 + b2 = 1 の交点も ( a, b ) = ( 1, ±1 ) で、この 3 つの曲線は同じ点 ( a, b ) = ( 1, ±1 ) で交わります。それに注意して図示すると以下のようになります。

2017年03月11日
名大入試問題 2017 (2)
2017 年名大入試問題の二問目です。個人的には一番悩まされた問題です。
-----
下図のような立方体を考える。この立方体の 8 つの頂点の上を点 P が次の規則で移動する。時刻 0 では点 P は頂点 A にいる。時刻が 1 増えるごとに点 P は、今いる頂点と辺で結ばれている頂点に等確率で移動する。例えば時刻 n で点 P が頂点 H にいるとすると、時刻 n + 1 では、それぞれ 1 / 3 の確率で頂点 D, E, G のいずれかにいる。自然数 n ≥ 1 に対して、(i) 点 P が時刻 n までの間一度も頂点 A に戻らず、かつ時刻 n で頂点 B, D, E のいずれかにいる確率を pn、(ii) 点 P が時刻 n までの間一度も頂点 A に戻らず、かつ時刻 n で頂点 C, F, H のいずれかにいる確率を qn、(iii) 点 P が時刻 n までの間一度も頂点 A に戻らず、かつ時刻 n で頂点 G にいる確率を rn とする。このとき、次の問に答えよ。
(1) p2, q2, r2 と p3, q3, r3 を求めよ。
(2) n ≥ 2 のとき、pn, qn, rn を求めよ。
(3) 自然数 m ≥ 1 に対して、点 P が時刻 2m で頂点 A に初めて戻る確率 sm を求めよ。
(4) 自然数 m ≥ 2 に対して、点 P が時刻 2m で頂点 A に戻るのがちょうど 2 回目となる確率を tm とする。このとき、tm < sm となる m をすべて求めよ。
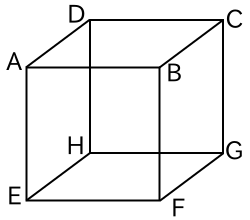
(1) 時刻 1 で点 P は B, D, E のいずれかにいるので p1 = 1 です。時刻 2 では B, D, E から A に戻る確率が 1 / 3、C, F, H へ移動する確率が 2 / 3 なので p2 = 0, q2 = 2 / 3, r2 = 0 となります。時刻 3 では C, F, H から G へ移動する確率が 1 / 3、B, D, E へ戻る確率が 2 / 3 で、q2 = 2 / 3 だったので p3 = 2/3 x 2/3 = 4 / 9、q3 = 0、r3 = 2/3 x 1/3 = 2 / 9 となります。
(2) n = 2m ( m は 1 以上の整数 ) のとき、点 P は C, F, H のいずれかにあるので p2m = r2m = 0 になります。また、n = 2m - 1 のとき、点 P は C, F, H のいずれにもないので q2m-1 = 0 です。
時刻 2m + 1 のとき、C, F, H にいた点 P は 2 / 3 の確率で B, D, E へ、1 / 3 の確率で G へ移動するので p2m+1 = (2/3)q2m、r2m+1 = (1/3)q2m が成り立ちます。また、時刻 2m + 2 のとき、B, D, E にいた点 P は 2 / 3 の確率で C, F, H へ、1 / 3 の確率で A へ移動し、G にいた場合は必ず C, F, H に移動するので q2m+2 = (2/3)p2m+1 + r2m+1 となります。従って、
q2m+2 = (2/3)・(2/3)q2m + (1/3)q2m = (7/9)q2m より q2m = (2/3)(7/9)m-1
であり、
p2m+1 = (4/9)(7/9)m-1、r2m+1 = (2/9)(7/9)m-1
となります。
(3) 時刻 2 のときは、(1) で述べたように 1 / 3 になります。それ以降は、時刻 2m - 1 のときに B, D, E にある確率 p2m-1 = (4/9)(7/9)m-2 に、A に移る確率 1 / 3 を掛ければ求められ、sm = (4/27)(7/9)m-2 になります。
(4) B, D, E にいる場合を X、C, F, H にいる場合を Y で表すことにします。まず、t1 = 0 は明らかです。t2 は A→X→A→X→A と遷移する場合しかないので、 1/3 x 1/3 = 1 / 9 です。s2 = 4 / 27 なので t2 < s2 となります。t3 は以下の二通りの確率の和になります。
A→X→A→X→Y→X→A 1/3 x 2/3 x 2/3 x 1/3 = 4 / 81
A→X→Y→X→A→X→A 2/3 x 2/3 x 1/3 x 1/3 = 4 / 81
よって、t3 = 8 / 81 で、s3 = 28 / 243 より t3 < s3 です。t4 の場合、
(a) A→X→A→X→Y→{ X or G }→Y→X→A
(b) A→X→Y→X→A→X→Y→X→A
(c) A→X→Y→{ X or G }→Y→X→A→X→A
となりますが ( X or G はいずれかに遷移するという意味です )、(a) の場合 A→X→A の部分とそれ以降に分けて考えると、それぞれ初めて A に戻る確率 s1, s3 に等しいので 1/3 x (4/27)(7/9) = 28 / 729 です。同様に (b) は 4/27 x 4/27 = 16 / 729、(c) は (4/27)(7/9) x 1/3 = 28 / 729 で、合わせて 72 / 729 になります。s4 = 196 / 2187 なので t4 > s4 で m = 4 のときは成り立ちません。
m = 4 の結果から、m ≥ 4 の場合の tm の計算式が以下のようになることがわかります。
tm = (1/3)・(4/27)(7/9)m-3 + (4/27)・(4/27)(7/9)m-4 + (4/27)(7/9)・(4/27)(7/9)m-5 + ... + (4/27)(7/9)m-3・(1/3)
= (2/3)(4/27)(7/9)m-3 + (4/27)2( m - 3 )(7/9)m-4
> [ (2/3)(9/7) + (4/27)(9/7)2 ](4/27)(7/9)m-2
= (162/147)(4/27)(7/9)m-2 > sm
従って、条件を満たす m は 2, 3 になります。
-----
下図のような立方体を考える。この立方体の 8 つの頂点の上を点 P が次の規則で移動する。時刻 0 では点 P は頂点 A にいる。時刻が 1 増えるごとに点 P は、今いる頂点と辺で結ばれている頂点に等確率で移動する。例えば時刻 n で点 P が頂点 H にいるとすると、時刻 n + 1 では、それぞれ 1 / 3 の確率で頂点 D, E, G のいずれかにいる。自然数 n ≥ 1 に対して、(i) 点 P が時刻 n までの間一度も頂点 A に戻らず、かつ時刻 n で頂点 B, D, E のいずれかにいる確率を pn、(ii) 点 P が時刻 n までの間一度も頂点 A に戻らず、かつ時刻 n で頂点 C, F, H のいずれかにいる確率を qn、(iii) 点 P が時刻 n までの間一度も頂点 A に戻らず、かつ時刻 n で頂点 G にいる確率を rn とする。このとき、次の問に答えよ。
(1) p2, q2, r2 と p3, q3, r3 を求めよ。
(2) n ≥ 2 のとき、pn, qn, rn を求めよ。
(3) 自然数 m ≥ 1 に対して、点 P が時刻 2m で頂点 A に初めて戻る確率 sm を求めよ。
(4) 自然数 m ≥ 2 に対して、点 P が時刻 2m で頂点 A に戻るのがちょうど 2 回目となる確率を tm とする。このとき、tm < sm となる m をすべて求めよ。

(1) 時刻 1 で点 P は B, D, E のいずれかにいるので p1 = 1 です。時刻 2 では B, D, E から A に戻る確率が 1 / 3、C, F, H へ移動する確率が 2 / 3 なので p2 = 0, q2 = 2 / 3, r2 = 0 となります。時刻 3 では C, F, H から G へ移動する確率が 1 / 3、B, D, E へ戻る確率が 2 / 3 で、q2 = 2 / 3 だったので p3 = 2/3 x 2/3 = 4 / 9、q3 = 0、r3 = 2/3 x 1/3 = 2 / 9 となります。
(2) n = 2m ( m は 1 以上の整数 ) のとき、点 P は C, F, H のいずれかにあるので p2m = r2m = 0 になります。また、n = 2m - 1 のとき、点 P は C, F, H のいずれにもないので q2m-1 = 0 です。
時刻 2m + 1 のとき、C, F, H にいた点 P は 2 / 3 の確率で B, D, E へ、1 / 3 の確率で G へ移動するので p2m+1 = (2/3)q2m、r2m+1 = (1/3)q2m が成り立ちます。また、時刻 2m + 2 のとき、B, D, E にいた点 P は 2 / 3 の確率で C, F, H へ、1 / 3 の確率で A へ移動し、G にいた場合は必ず C, F, H に移動するので q2m+2 = (2/3)p2m+1 + r2m+1 となります。従って、
q2m+2 = (2/3)・(2/3)q2m + (1/3)q2m = (7/9)q2m より q2m = (2/3)(7/9)m-1
であり、
p2m+1 = (4/9)(7/9)m-1、r2m+1 = (2/9)(7/9)m-1
となります。
(3) 時刻 2 のときは、(1) で述べたように 1 / 3 になります。それ以降は、時刻 2m - 1 のときに B, D, E にある確率 p2m-1 = (4/9)(7/9)m-2 に、A に移る確率 1 / 3 を掛ければ求められ、sm = (4/27)(7/9)m-2 になります。
(4) B, D, E にいる場合を X、C, F, H にいる場合を Y で表すことにします。まず、t1 = 0 は明らかです。t2 は A→X→A→X→A と遷移する場合しかないので、 1/3 x 1/3 = 1 / 9 です。s2 = 4 / 27 なので t2 < s2 となります。t3 は以下の二通りの確率の和になります。
A→X→A→X→Y→X→A 1/3 x 2/3 x 2/3 x 1/3 = 4 / 81
A→X→Y→X→A→X→A 2/3 x 2/3 x 1/3 x 1/3 = 4 / 81
よって、t3 = 8 / 81 で、s3 = 28 / 243 より t3 < s3 です。t4 の場合、
(a) A→X→A→X→Y→{ X or G }→Y→X→A
(b) A→X→Y→X→A→X→Y→X→A
(c) A→X→Y→{ X or G }→Y→X→A→X→A
となりますが ( X or G はいずれかに遷移するという意味です )、(a) の場合 A→X→A の部分とそれ以降に分けて考えると、それぞれ初めて A に戻る確率 s1, s3 に等しいので 1/3 x (4/27)(7/9) = 28 / 729 です。同様に (b) は 4/27 x 4/27 = 16 / 729、(c) は (4/27)(7/9) x 1/3 = 28 / 729 で、合わせて 72 / 729 になります。s4 = 196 / 2187 なので t4 > s4 で m = 4 のときは成り立ちません。
m = 4 の結果から、m ≥ 4 の場合の tm の計算式が以下のようになることがわかります。
tm = (1/3)・(4/27)(7/9)m-3 + (4/27)・(4/27)(7/9)m-4 + (4/27)(7/9)・(4/27)(7/9)m-5 + ... + (4/27)(7/9)m-3・(1/3)
= (2/3)(4/27)(7/9)m-3 + (4/27)2( m - 3 )(7/9)m-4
> [ (2/3)(9/7) + (4/27)(9/7)2 ](4/27)(7/9)m-2
= (162/147)(4/27)(7/9)m-2 > sm
従って、条件を満たす m は 2, 3 になります。
2017年03月05日
名大入試問題 2017 (1)
3 月になりました。だいぶ暖かくなりましたね。
本日、「アルゴリズムのコーナー」を更新しました。内容は予定通り「自己組織化写像(SOM)」です。今回はかなりボリュームが少なくなりました。他に面白いネタがあれば追加したいのですが、あいにく今のところ思い浮かびません。結構おもしろいアルゴリズムで、他にもいろいろな応用があると思うのですが。。。
新聞に載っていた名大の入試問題を今年も解いてみました。まずは一問目から。今回は解答もチェックしていますので答えは合ってます。
-----
不等式 0 < a < 1 を満たす定数 a に対して、曲線 C : y = a - 1 - log x ( x > 0 ) を考える。s を正の定数とし、曲線 C 上の点 P( s, a - 1 - log s ) における接線が x 軸、y 軸と交わる点をそれぞれ ( u(s), 0 ), ( 0, v(s) ) とする。このとき、次の問いに答えよ。必要があれば、lim{x→0} x log x = 0 を証明なしで使ってよい (2017年 名大)。
(1) 関数 u(s), v(s) を s の式で表せ。
(2) 関数 t = u(s), t = v(s) の 2 つのグラフを、領域・凹凸および交点の座標に注意して、同じ st 平面上に図示せよ。
(3) 関数 t = u(s), t = v(s) の 2 つのグラフで囲まれた図形を t 軸のまわりに 1 回転させてできる立体の体積を求めよ。
(1) y' = -1 / x より P の接線は
y = (-1/s)( x - s ) + a - 1 - log s = (-1/s)x + a - log s
となります。y = 0 のとき
x = s( a - log s ) より u(s) = s( a - log s )
x = 0 のとき
y = a - log s より v(s) = a - log s
となります。
(2) u'(s) = a - log s - 1, u''(s) = -1 / s < 0 より u(s) は 0 < s < ea-1 で増加、s = ea-1 のとき極値をとり、s > ea-1 で減少します。また、s = 0, ea のとき u(s) = 0 となります。
v'(s) = -1/s < 0, v''(s) = 1 / s2 > 0 v(s) は単調減少で下に凸であり、s = ea のとき v(s) = 0 です。
u(s) と v(s) の交点は、s( a - log s ) = a - log s より a - log s ≠ 0 のとき s = 1、a - log s = 0 のとき s = ea です。よって、グラフは下図のようになります。
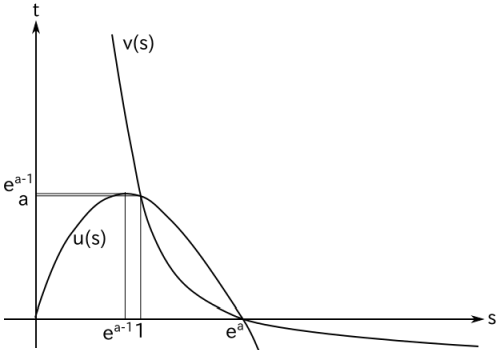
(3) t = v(s) = a - log s より s = ea-t なので、v(s) を t 軸のまわりに回転させたときの 0 ≤ t ≤ a での回転体の体積は
π∫{0→a} e2a-2t dt
= π[ (-1/2)e2a-2t ]{0→a}
= π( -1/2 + e2a / 2 )
= (π/2)( e2a - 1 )
となります。また、t = u(s) s( a - log s ) より dt = ( a - log s - 1 )ds、t = 0 のとき s = ea、t = a のとき s = 1 なので、回転体の体積は
π∫{0→a} s2 dt
= π∫{ea→1} s2( a - log s - 1 ) ds
= π{ [ (1/3)( a - 1 )s3 ]{ea→1} - ∫{ea→1} s2 log s ds }
で計算できます。
∫{ea→1} s2 log s ds
= [ (1/3)s3log s ]{ea→1} - (1/3)∫{ea→1} s2 ds
= -(1/3)ae3a - (1/3)[ (1/3)s3 ]{ea→1}
= -(1/3)ae3a - 1 / 9 + (1/9)e3a
なので、
π∫{0→a} s2 dt
= π{ (1/3)( a - 1 )( 1 - e3a ) + (1/3)ae3a + 1 / 9 - (1/9)e3a }
= π[ (2/9)e3a - 2 / 9 + (1/3)a ]
となり、求める体積は
= π[ (2/9)e3a - 2 / 9 + (1/3)a ] - (π/2)( e2a - 1 )
= (π/18)( 4e3a - 9e2a + 6a + 5 )
となります。
回転体の体積の求め方をすっかり忘れておりました。ググって調べたのは内緒です。
本日、「アルゴリズムのコーナー」を更新しました。内容は予定通り「自己組織化写像(SOM)」です。今回はかなりボリュームが少なくなりました。他に面白いネタがあれば追加したいのですが、あいにく今のところ思い浮かびません。結構おもしろいアルゴリズムで、他にもいろいろな応用があると思うのですが。。。
新聞に載っていた名大の入試問題を今年も解いてみました。まずは一問目から。今回は解答もチェックしていますので答えは合ってます。
-----
不等式 0 < a < 1 を満たす定数 a に対して、曲線 C : y = a - 1 - log x ( x > 0 ) を考える。s を正の定数とし、曲線 C 上の点 P( s, a - 1 - log s ) における接線が x 軸、y 軸と交わる点をそれぞれ ( u(s), 0 ), ( 0, v(s) ) とする。このとき、次の問いに答えよ。必要があれば、lim{x→0} x log x = 0 を証明なしで使ってよい (2017年 名大)。
(1) 関数 u(s), v(s) を s の式で表せ。
(2) 関数 t = u(s), t = v(s) の 2 つのグラフを、領域・凹凸および交点の座標に注意して、同じ st 平面上に図示せよ。
(3) 関数 t = u(s), t = v(s) の 2 つのグラフで囲まれた図形を t 軸のまわりに 1 回転させてできる立体の体積を求めよ。
(1) y' = -1 / x より P の接線は
y = (-1/s)( x - s ) + a - 1 - log s = (-1/s)x + a - log s
となります。y = 0 のとき
x = s( a - log s ) より u(s) = s( a - log s )
x = 0 のとき
y = a - log s より v(s) = a - log s
となります。
(2) u'(s) = a - log s - 1, u''(s) = -1 / s < 0 より u(s) は 0 < s < ea-1 で増加、s = ea-1 のとき極値をとり、s > ea-1 で減少します。また、s = 0, ea のとき u(s) = 0 となります。
v'(s) = -1/s < 0, v''(s) = 1 / s2 > 0 v(s) は単調減少で下に凸であり、s = ea のとき v(s) = 0 です。
u(s) と v(s) の交点は、s( a - log s ) = a - log s より a - log s ≠ 0 のとき s = 1、a - log s = 0 のとき s = ea です。よって、グラフは下図のようになります。

(3) t = v(s) = a - log s より s = ea-t なので、v(s) を t 軸のまわりに回転させたときの 0 ≤ t ≤ a での回転体の体積は
π∫{0→a} e2a-2t dt
= π[ (-1/2)e2a-2t ]{0→a}
= π( -1/2 + e2a / 2 )
= (π/2)( e2a - 1 )
となります。また、t = u(s) s( a - log s ) より dt = ( a - log s - 1 )ds、t = 0 のとき s = ea、t = a のとき s = 1 なので、回転体の体積は
π∫{0→a} s2 dt
= π∫{ea→1} s2( a - log s - 1 ) ds
= π{ [ (1/3)( a - 1 )s3 ]{ea→1} - ∫{ea→1} s2 log s ds }
で計算できます。
∫{ea→1} s2 log s ds
= [ (1/3)s3log s ]{ea→1} - (1/3)∫{ea→1} s2 ds
= -(1/3)ae3a - (1/3)[ (1/3)s3 ]{ea→1}
= -(1/3)ae3a - 1 / 9 + (1/9)e3a
なので、
π∫{0→a} s2 dt
= π{ (1/3)( a - 1 )( 1 - e3a ) + (1/3)ae3a + 1 / 9 - (1/9)e3a }
= π[ (2/9)e3a - 2 / 9 + (1/3)a ]
となり、求める体積は
= π[ (2/9)e3a - 2 / 9 + (1/3)a ] - (π/2)( e2a - 1 )
= (π/18)( 4e3a - 9e2a + 6a + 5 )
となります。
回転体の体積の求め方をすっかり忘れておりました。ググって調べたのは内緒です。
2017年02月26日
光通信
先週末は歓迎会で飲んでました。
ケーブルテレビが光ファイバーに配線切替されるということで工事の下見がありました。メールアドレスが有料になるものの月額はそのままで通信速度が速くなるということで非常にオトクな話です。しかし、ショックだったのが無線 LAN 機能標準装備ということ。ルータが最近故障して買い直したばかりだったので非常に損した気分です。もう少し故障するのが遅ければ。。。
「数学問題bot」から東大の問題です。かなり悩みました。例によって合っている保証はありません。
-----
各世代ごとに、各個体が他の個体とは独立に、確率 p [ 0 < p < 1 ] で 1 個、確率 1 - p で 2 個の新しい個体を次の世代に残し、それ自身消滅する細胞がある。第 0 世代に 1 個だった細胞が第 n [ n ∈ N ] 世代に m 個になる確率を Pn(m) と書く。Pn(1), Pn(2), Pn(3) を求めよ ( 84 東大 )
下図は、第 4 世代まで、3 個まで分裂するときの確率を表したものです。
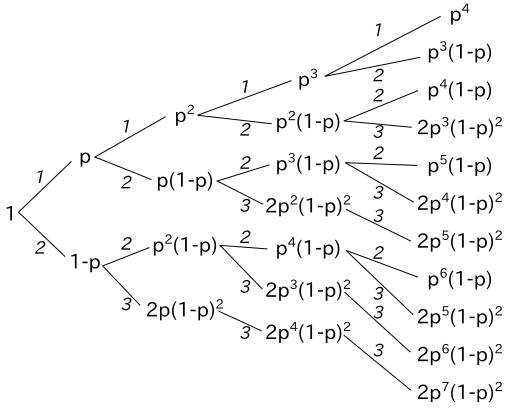
前の世代が 1 個の場合、次の世代では 1 個か 2 個のいずれかにしかなりません。次の世代が 1 個になる確率は前の確率に p を掛けたものになります。また、2 個になる確率は前の確率に p( 1 - p ) を掛けたものになります。
前の世代が 2 個の場合、次の世代では 2, 3, 4 個のいずれかになります。次の世代が 2 個になる確率は前の確率に p2 を掛けたものになります。また、3 個になる確率は前の確率に 2p( 1 - p ) を掛けたものになります。
前の世代が 3 個の場合、次の世代では 3 から 6 個までのいずれかになります。次の世代が 3 個になる確率は前の確率に p3 を掛けたものになります。
1 個の個体を残す事象を A、2 個の個体を残す事象を B とします。n 回目で 1 つだけになるのは常に事象 A が発生した場合なので、その確率は pn です。よって、Pn(1) = pn となります。
n 回目で 2 個となるのは、n - 1 回目で 1 個であった場合に事象 B が発生する場合と、2 個であった場合に A, B が各々発生した場合に限られます。従って、各回について 2 個になる場合は 1 つずつ増え、1 個から 2 個に変化した場合、それまでは pn-1 の確率で発生していたので pn-1( p - 1 ) の確率になります。また、2 個のままである場合、それまでの確率に p2 を掛けた確率になります。
上図から、Pn(2) = ( pn-1 + pn + ... + p2n-2 )( 1 - p ) と仮定してみます。このとき、P1(2) = 1 - p で成り立ちます。
n + 1 回目では、各事象に対して p2 を掛けたものに 1 個から 2 個に増えた場合の確率 pn( 1 - p ) を加えた値になるので
Pn+1(2)
= pn( 1 - p ) + p2( pn-1 + pn + ... + p2n-2 )( 1 - p )
= ( pn + pn+1 + pn+2 + ... + p2(n+1)-2 )( 1 - p )
となり、帰納法により正しいことがわかります。
Pn(2) = ( pn-1 + pn + ... + p2n-2 )( 1 - p )
pPn(2) = ( pn + pn+1 + ... + p2n-1 )( 1 - p ) より
( 1 - p )Pn(2) = ( pn-1 - p2n-1 )( 1 - p )
よって Pn(2) = pn-1 - p2n-1 = pn-1( 1 - pn ) となります。
n 回目で 3 個となるのは、n - 1 回目で 2 個であった場合に A, B の両方が発生した場合と、3 個であった場合に全てにおいて A が発生した場合に限られます。n 回目で 2 個から 3 個になる確率は 2 個になる確率 pn-2( 1 - pn-1 ) に 2p( 1 - p ) を掛けることで求められ、3 個のままである確率は Pn-1(3) に p3 を掛けることで求められるので、次の漸化式が成り立つことになります。
Pn(3) = p3Pn-1(3) + 2pn-1( 1 - p )( 1 - pn-1 )
これを解くと、
Pn(3)
= p3Pn-1(3) + 2pn-1( 1 - p )( 1 - pn-1 )
= p3[ p3Pn-2(3) + 2pn-2( 1 - p )( 1 - pn-2 ) ] + 2pn-1( 1 - p )( 1 - pn-1 )
= p6Pn-2(3) + 2pn+1( 1 - p )( 1 - pn-2 ) + 2pn-1( 1 - p )( 1 - pn-1 )
= p6[ p3Pn-3(3) + 2pn-3( 1 - p )( 1 - pn-3 ) ] + 2pn+1( 1 - p )( 1 - pn-2 ) + 2pn-1( 1 - p )( 1 - pn-1 )
= p9Pn-3(3) + 2pn+3( 1 - p )( 1 - pn-3 ) + 2pn+1( 1 - p )( 1 - pn-2 ) + 2pn-1( 1 - p )( 1 - pn-1 )
= ...
= p3(n-1)P1(3) + 23p-5( 1 - p )2 + ... + 2pn+1( 1 - p )( 1 - pn-2 ) + 2pn-1( 1 - p )( 1 - pn-1 )
= Σk{1→n-1}( 2p3n-3-2k( 1 - p )( 1 - pk ) )
となります。式を展開して
Pn(3) = ( 1 - p )Σk{1→n-1}( 2p3n-3-2k - 2p3n-3-k ) ≡ ( 1 - p )( S1 + S2 )
とすると、
S1 = 2p3n-5 + 2p3n-7 + ... + 2pn-1
p2S1 = 2p3n-3 + 2p3n-5 + ... + 2pn+1
で、辺々引いて
( 1 - p2 )S1 = 2pn-1 - 2p3n-3
S1 = 2pn-1( 1 - p2n-2 ) / ( 1 - p2 )
となります。また、
S2 = 2p3n-4 + 2p3n-5 + ... + 2p2n-2
pS2 = 2p3n-3 + 2p3n-4 + ... + 2p2n-1
で、辺々引いて
( 1 - p )S2 = 2p2n-2 - 2p3n-3
S2 = 2p2n-2( 1 - pn-1 ) / ( 1 - p )
なので、
Pn(3)
= 2pn-1( 1 - p2n-2 ) / ( 1 + p ) - 2p2n-2( 1 - pn-1 )
= 2pn-1[ ( 1 - p2n-2 ) - ( 1 + p )( pn-1 - p2n-2 ] / ( 1 + p )
= 2pn-1( 1 - p2n-2 - pn-1 + p2n-2 - pn + p2n-1 ) / ( 1 + p )
= 2pn-1[ ( 1 - pn-1 ) - pn( 1 - pn-1 ) ] / ( 1 + p )
= 2pn-1( 1 - pn )( 1 - pn-1 ) / ( 1 + p )
となります。
ケーブルテレビが光ファイバーに配線切替されるということで工事の下見がありました。メールアドレスが有料になるものの月額はそのままで通信速度が速くなるということで非常にオトクな話です。しかし、ショックだったのが無線 LAN 機能標準装備ということ。ルータが最近故障して買い直したばかりだったので非常に損した気分です。もう少し故障するのが遅ければ。。。
「数学問題bot」から東大の問題です。かなり悩みました。例によって合っている保証はありません。
-----
各世代ごとに、各個体が他の個体とは独立に、確率 p [ 0 < p < 1 ] で 1 個、確率 1 - p で 2 個の新しい個体を次の世代に残し、それ自身消滅する細胞がある。第 0 世代に 1 個だった細胞が第 n [ n ∈ N ] 世代に m 個になる確率を Pn(m) と書く。Pn(1), Pn(2), Pn(3) を求めよ ( 84 東大 )
下図は、第 4 世代まで、3 個まで分裂するときの確率を表したものです。

前の世代が 1 個の場合、次の世代では 1 個か 2 個のいずれかにしかなりません。次の世代が 1 個になる確率は前の確率に p を掛けたものになります。また、2 個になる確率は前の確率に p( 1 - p ) を掛けたものになります。
前の世代が 2 個の場合、次の世代では 2, 3, 4 個のいずれかになります。次の世代が 2 個になる確率は前の確率に p2 を掛けたものになります。また、3 個になる確率は前の確率に 2p( 1 - p ) を掛けたものになります。
前の世代が 3 個の場合、次の世代では 3 から 6 個までのいずれかになります。次の世代が 3 個になる確率は前の確率に p3 を掛けたものになります。
1 個の個体を残す事象を A、2 個の個体を残す事象を B とします。n 回目で 1 つだけになるのは常に事象 A が発生した場合なので、その確率は pn です。よって、Pn(1) = pn となります。
n 回目で 2 個となるのは、n - 1 回目で 1 個であった場合に事象 B が発生する場合と、2 個であった場合に A, B が各々発生した場合に限られます。従って、各回について 2 個になる場合は 1 つずつ増え、1 個から 2 個に変化した場合、それまでは pn-1 の確率で発生していたので pn-1( p - 1 ) の確率になります。また、2 個のままである場合、それまでの確率に p2 を掛けた確率になります。
上図から、Pn(2) = ( pn-1 + pn + ... + p2n-2 )( 1 - p ) と仮定してみます。このとき、P1(2) = 1 - p で成り立ちます。
n + 1 回目では、各事象に対して p2 を掛けたものに 1 個から 2 個に増えた場合の確率 pn( 1 - p ) を加えた値になるので
Pn+1(2)
= pn( 1 - p ) + p2( pn-1 + pn + ... + p2n-2 )( 1 - p )
= ( pn + pn+1 + pn+2 + ... + p2(n+1)-2 )( 1 - p )
となり、帰納法により正しいことがわかります。
Pn(2) = ( pn-1 + pn + ... + p2n-2 )( 1 - p )
pPn(2) = ( pn + pn+1 + ... + p2n-1 )( 1 - p ) より
( 1 - p )Pn(2) = ( pn-1 - p2n-1 )( 1 - p )
よって Pn(2) = pn-1 - p2n-1 = pn-1( 1 - pn ) となります。
n 回目で 3 個となるのは、n - 1 回目で 2 個であった場合に A, B の両方が発生した場合と、3 個であった場合に全てにおいて A が発生した場合に限られます。n 回目で 2 個から 3 個になる確率は 2 個になる確率 pn-2( 1 - pn-1 ) に 2p( 1 - p ) を掛けることで求められ、3 個のままである確率は Pn-1(3) に p3 を掛けることで求められるので、次の漸化式が成り立つことになります。
Pn(3) = p3Pn-1(3) + 2pn-1( 1 - p )( 1 - pn-1 )
これを解くと、
Pn(3)
= p3Pn-1(3) + 2pn-1( 1 - p )( 1 - pn-1 )
= p3[ p3Pn-2(3) + 2pn-2( 1 - p )( 1 - pn-2 ) ] + 2pn-1( 1 - p )( 1 - pn-1 )
= p6Pn-2(3) + 2pn+1( 1 - p )( 1 - pn-2 ) + 2pn-1( 1 - p )( 1 - pn-1 )
= p6[ p3Pn-3(3) + 2pn-3( 1 - p )( 1 - pn-3 ) ] + 2pn+1( 1 - p )( 1 - pn-2 ) + 2pn-1( 1 - p )( 1 - pn-1 )
= p9Pn-3(3) + 2pn+3( 1 - p )( 1 - pn-3 ) + 2pn+1( 1 - p )( 1 - pn-2 ) + 2pn-1( 1 - p )( 1 - pn-1 )
= ...
= p3(n-1)P1(3) + 23p-5( 1 - p )2 + ... + 2pn+1( 1 - p )( 1 - pn-2 ) + 2pn-1( 1 - p )( 1 - pn-1 )
= Σk{1→n-1}( 2p3n-3-2k( 1 - p )( 1 - pk ) )
となります。式を展開して
Pn(3) = ( 1 - p )Σk{1→n-1}( 2p3n-3-2k - 2p3n-3-k ) ≡ ( 1 - p )( S1 + S2 )
とすると、
S1 = 2p3n-5 + 2p3n-7 + ... + 2pn-1
p2S1 = 2p3n-3 + 2p3n-5 + ... + 2pn+1
で、辺々引いて
( 1 - p2 )S1 = 2pn-1 - 2p3n-3
S1 = 2pn-1( 1 - p2n-2 ) / ( 1 - p2 )
となります。また、
S2 = 2p3n-4 + 2p3n-5 + ... + 2p2n-2
pS2 = 2p3n-3 + 2p3n-4 + ... + 2p2n-1
で、辺々引いて
( 1 - p )S2 = 2p2n-2 - 2p3n-3
S2 = 2p2n-2( 1 - pn-1 ) / ( 1 - p )
なので、
Pn(3)
= 2pn-1( 1 - p2n-2 ) / ( 1 + p ) - 2p2n-2( 1 - pn-1 )
= 2pn-1[ ( 1 - p2n-2 ) - ( 1 + p )( pn-1 - p2n-2 ] / ( 1 + p )
= 2pn-1( 1 - p2n-2 - pn-1 + p2n-2 - pn + p2n-1 ) / ( 1 + p )
= 2pn-1[ ( 1 - pn-1 ) - pn( 1 - pn-1 ) ] / ( 1 + p )
= 2pn-1( 1 - pn )( 1 - pn-1 ) / ( 1 + p )
となります。
2017年01月22日
大寒
大寒に入って、あいかわらず寒い毎日です。
大相撲初場所は稀勢の里が見事に優勝しました。横綱になれば、日本人としては 19 年ぶりの横綱誕生になるのだそうです。最後に横綱になったのが若乃花というから本当に久々ですね。
日本では相撲が盛り上がりを見せていましたが、世界中はトランプ大統領の就任に対して大規模なデモが行われていたようです。何か異常な状況ですが、本当に大丈夫なんでしょうかね、このままで。
「数学問題bot」から、京大の問題です。例によって合っている保証はありません。
-----
極方程式 r = 1 + cos θ ( 0 ≤ θ ≤ π ) で表される曲線の長さを求めよ ( 09 京都・理甲 )
x = r cos θ
= ( 1 + cos θ )cos θ
= cos θ + ( 1 / 2 )( 2cos2 θ - 1 ) + 1 / 2
= ( 1 / 2 )cos 2θ + cos θ + 1 / 2
y = r sin θ
= ( 1 + cos θ )sin θ
= sin θ + ( 1 / 2 )( 2sin θcos θ )
= ( 1 / 2 )sin 2θ + sin θ
より
dx / dθ = -sin 2θ - sin θ
dy / dθ = cos 2θ + cos θ
となります。従って、曲線の長さは
∫{0→π} [ ( dx / dθ )2 + ( dy / dθ )2 ]1/2 dθ
= ∫{0→π} [ ( -sin 2θ - sin θ )2 + ( cos 2θ + cos θ )2 ]1/2 dθ
= ∫{0→π} ( sin2 2θ + 2sin 2θsin θ + sin2 θ + cos2 2θ + 2cos 2θcos θ + cos2 θ )1/2 dθ
を解くことで求められます。
cos 2θcos θ + sin 2θsin θ
= cos ( 2θ - θ ) = cos θ より
(与式) = ∫{0→π} ( 2 + 2cos2 θ )1/2 dθ
t = cos θ とすると、
dt / dθ = -sin θ ( 0 ≤ θ ≤ π より sin θ ≥ 0 )
= -( 1 - cos2 θ )1/2
= -( 1 - t2 )1/2
で、θ = 0 のとき t = 1、θ = π のとき t = -1 なので、
(与式) = √2∫{1→-1} ( 1 + t )1/2・[ - 1 / ( 1 - t2 )1/2 ] dt
= √2∫{-1→1} ( 1 - t )-1/2 dt
= √2[ -2( 1 - t )1/2 ]{-1→1}
= √2( 0 + 2√2 ) = 4
となります。
大相撲初場所は稀勢の里が見事に優勝しました。横綱になれば、日本人としては 19 年ぶりの横綱誕生になるのだそうです。最後に横綱になったのが若乃花というから本当に久々ですね。
日本では相撲が盛り上がりを見せていましたが、世界中はトランプ大統領の就任に対して大規模なデモが行われていたようです。何か異常な状況ですが、本当に大丈夫なんでしょうかね、このままで。
「数学問題bot」から、京大の問題です。例によって合っている保証はありません。
-----
極方程式 r = 1 + cos θ ( 0 ≤ θ ≤ π ) で表される曲線の長さを求めよ ( 09 京都・理甲 )
x = r cos θ
= ( 1 + cos θ )cos θ
= cos θ + ( 1 / 2 )( 2cos2 θ - 1 ) + 1 / 2
= ( 1 / 2 )cos 2θ + cos θ + 1 / 2
y = r sin θ
= ( 1 + cos θ )sin θ
= sin θ + ( 1 / 2 )( 2sin θcos θ )
= ( 1 / 2 )sin 2θ + sin θ
より
dx / dθ = -sin 2θ - sin θ
dy / dθ = cos 2θ + cos θ
となります。従って、曲線の長さは
∫{0→π} [ ( dx / dθ )2 + ( dy / dθ )2 ]1/2 dθ
= ∫{0→π} [ ( -sin 2θ - sin θ )2 + ( cos 2θ + cos θ )2 ]1/2 dθ
= ∫{0→π} ( sin2 2θ + 2sin 2θsin θ + sin2 θ + cos2 2θ + 2cos 2θcos θ + cos2 θ )1/2 dθ
を解くことで求められます。
cos 2θcos θ + sin 2θsin θ
= cos ( 2θ - θ ) = cos θ より
(与式) = ∫{0→π} ( 2 + 2cos2 θ )1/2 dθ
t = cos θ とすると、
dt / dθ = -sin θ ( 0 ≤ θ ≤ π より sin θ ≥ 0 )
= -( 1 - cos2 θ )1/2
= -( 1 - t2 )1/2
で、θ = 0 のとき t = 1、θ = π のとき t = -1 なので、
(与式) = √2∫{1→-1} ( 1 + t )1/2・[ - 1 / ( 1 - t2 )1/2 ] dt
= √2∫{-1→1} ( 1 - t )-1/2 dt
= √2[ -2( 1 - t )1/2 ]{-1→1}
= √2( 0 + 2√2 ) = 4
となります。
2017年01月15日
寒波到来
昨日から名古屋も大雪でした。
休日中は近くに出かけただけでほとんど家にいました。雪道には慣れていないので、ほんの少し出かけるだけでも大変です。雪は明日まで続くということで、会社にたどり着けるか心配ですね。運悪く、センター試験とも重なって受験生にとっては大変な二日間だったと思います。いつも思うんですけど、なぜこういう時期に試験をするんでしょうかね。
「数学問題bot」から、センター試験の問題を選んでみました。一応、検算はしてますが、合っている保証はありません。
-----
二次関数 y = -x2 + ( 2a + 4 )x + b の頂点座標が直線 y = -4x - 1 上にあるとする。この二次関数の 0 ≤ x ≤ 4 における最小値が -22 のとき、a の値とそのときの最大値を求めよ ( 12 センター数学 1A )
y = -x2 + ( 2a + 4 )x + b = -[ x - ( a + 2 ) ]2 + ( a + 2 )2 + b
より二次関数の頂点は ( a + 2, ( a + 2 )2 + b ) になります。この座標が y = -4x - 1 上にあるので
( a + 2 )2 + b = -4( a + 2 ) - 1 より
b = -a2 - 8a - 13
となります。x = 0 のとき y = b = -a2 - 8a - 13、x = 4 のとき y = 8a + b = -a2 - 13 なので、a > 0 ならば x = 0 のとき、a < 0 ならば x = 4 のとき最小値となります。
前者の場合、-a2 - 8a - 13 = -22 より a2 + 8a - 9 = 0 なので a = -9, 1 で、a > 0 より a = 1 となります。このとき、b = -22 で、
y = -( x - 3 )2 + 32 - 22 = -( x - 3 )2 - 13
なので、最大値は -13 となります。
後者の場合は -a2 - 13 = -22 より a2 = 9 なので a = ±3 で、a < 0 より a = -3 となります。このとき、b = 2 で、
y = -( x + 1 )2 + ( -1 )2 + 2 = -( x + 1 )2 + 3
なので、最大値は 3 となります。
休日中は近くに出かけただけでほとんど家にいました。雪道には慣れていないので、ほんの少し出かけるだけでも大変です。雪は明日まで続くということで、会社にたどり着けるか心配ですね。運悪く、センター試験とも重なって受験生にとっては大変な二日間だったと思います。いつも思うんですけど、なぜこういう時期に試験をするんでしょうかね。
「数学問題bot」から、センター試験の問題を選んでみました。一応、検算はしてますが、合っている保証はありません。
-----
二次関数 y = -x2 + ( 2a + 4 )x + b の頂点座標が直線 y = -4x - 1 上にあるとする。この二次関数の 0 ≤ x ≤ 4 における最小値が -22 のとき、a の値とそのときの最大値を求めよ ( 12 センター数学 1A )
y = -x2 + ( 2a + 4 )x + b = -[ x - ( a + 2 ) ]2 + ( a + 2 )2 + b
より二次関数の頂点は ( a + 2, ( a + 2 )2 + b ) になります。この座標が y = -4x - 1 上にあるので
( a + 2 )2 + b = -4( a + 2 ) - 1 より
b = -a2 - 8a - 13
となります。x = 0 のとき y = b = -a2 - 8a - 13、x = 4 のとき y = 8a + b = -a2 - 13 なので、a > 0 ならば x = 0 のとき、a < 0 ならば x = 4 のとき最小値となります。
前者の場合、-a2 - 8a - 13 = -22 より a2 + 8a - 9 = 0 なので a = -9, 1 で、a > 0 より a = 1 となります。このとき、b = -22 で、
y = -( x - 3 )2 + 32 - 22 = -( x - 3 )2 - 13
なので、最大値は -13 となります。
後者の場合は -a2 - 13 = -22 より a2 = 9 なので a = ±3 で、a < 0 より a = -3 となります。このとき、b = 2 で、
y = -( x + 1 )2 + ( -1 )2 + 2 = -( x + 1 )2 + 3
なので、最大値は 3 となります。
2017年01月09日
参考書の問題
今日はわりと暖かい一日でした。散歩するにはいい日でしたね。夕方から少し雨が降りましたが。
今回は、とある参考書にあった問題です。大学入試にも出そうな内容ですね。
-----
1) 2r - 1 が素数とすると、r は素数であることを示せ。
2) 2r + 1 が素数であれば、r は 2 のベキであることを示せ。
1) 対偶となる「r が合成数なら 2r - 1 は合成数」を示します。r = mn ( m, n は 2 以上の整数 ) とすると、
2r - 1 = 2mn - 1 = ( 2n )m - 1
となります。2n = K とすると、
2r - 1 = Km - 1 = ( K - 1 )( Km-1 + Km-2 + ... + 1 )
なので、2r - 1 は必ず合成数となります。
2) 対偶となる「r が 2 のベキでないなら 2r + 1 は合成数」を示します。r = m( 2n + 1 ) ( m, n は 1 以上の整数 ) とすると、
2r + 1 = 2m(2n+1) + 1 = ( 2m )2n+1 + 1
となります。2m = K とすると、
2r + 1 = K2n+1 + 1 = ( K + 1 )( K2n - K2n-1 + ... - K + 1 )
なので、2r + 1 は必ず合成数となります。
2r - 1 の形の素数を「メルセンヌ数」、2r + 1 の形の素数を「フェルマーの素数」というそうです。
( 出典元 「群・環・体入門」 新妻弘・木村哲三 著 共立出版 )
今回は、とある参考書にあった問題です。大学入試にも出そうな内容ですね。
-----
1) 2r - 1 が素数とすると、r は素数であることを示せ。
2) 2r + 1 が素数であれば、r は 2 のベキであることを示せ。
1) 対偶となる「r が合成数なら 2r - 1 は合成数」を示します。r = mn ( m, n は 2 以上の整数 ) とすると、
2r - 1 = 2mn - 1 = ( 2n )m - 1
となります。2n = K とすると、
2r - 1 = Km - 1 = ( K - 1 )( Km-1 + Km-2 + ... + 1 )
なので、2r - 1 は必ず合成数となります。
2) 対偶となる「r が 2 のベキでないなら 2r + 1 は合成数」を示します。r = m( 2n + 1 ) ( m, n は 1 以上の整数 ) とすると、
2r + 1 = 2m(2n+1) + 1 = ( 2m )2n+1 + 1
となります。2m = K とすると、
2r + 1 = K2n+1 + 1 = ( K + 1 )( K2n - K2n-1 + ... - K + 1 )
なので、2r + 1 は必ず合成数となります。
2r - 1 の形の素数を「メルセンヌ数」、2r + 1 の形の素数を「フェルマーの素数」というそうです。
( 出典元 「群・環・体入門」 新妻弘・木村哲三 著 共立出版 )
2016年12月18日
今年最後の更新
「アルゴリズムのコーナー」にて新たなテーマとして「パターン認識」を追加しました。最初は「凝集型クラスタリング」を紹介しています。これが今年最後の更新になりそうです。
予定より内容がふくらんでしまい、だいぶ時間がかかってしまいましたが何とか今年中に公開することができました。次のお題もだいたいは決まっているものの、どこで区切りを付けるか少々悩んでいます。まあ、今度はのんびりと進めることにします。
「数学問題 bot ( 個人用 )」から京大の問題を選んでみました。例によって合っている保証はありません。
-----
(1) 21/3 が無理数であることを示せ。
(2) P(x) は有理数を係数とする x の多項式で、P(21/3) = 0 を満たしているとする。このとき P(x) は x3 - 2 で割り切れることを証明せよ ( 2012 京大 )
(1) 21/3 = a / b ( 但し、a, b は互いに素な整数で b ≠ 0 とする ) と仮定します。この等式が成り立てば 21/3 は有理数です。このとき、両辺を 3 乗して
2 = a3 / b3 より a3 = 2b3
となり、a は 2 を素因数に持つことになります。a = 2c とすると、
8c3 = 2b3 より b3 = 4c3
となり、b は 2 を素因数に持つことになるので a, b が互いに素であるという仮定に反します。したがって、21/3 は有理数ではなく、無理数であることが証明されました。
(2) P(21/3) = 0 より P(x) は因数 x - 21/3 を持ちます。そこで
P(x) = ( x - 21/3 )Q(x)
Q(x) = Σk{0→n-1}( akxk )
とすると、
P(x)
= ( x - 21/3 )( an-1xn-1 + an-2xn-2 + ... + a0 )
= an-1xn + ( an-2 - 21/3an-1 )xn-1 + ... + ( a0 - 21/3a1 )x - 21/3a0
となります。P(x) の係数は有理数なので、Q を自然数全体の集合としたとき ak-1 - 21/3ak ∈ Q, an-1 ∈ Q, 21/3a0 ∈ Q が成り立つ必要があります。しかし、21/3 は無理数なので、
(i) ak = 0 ( 0 < k < n ) かつ 21/3a0 ∈ Q
または
(ii) ak-1 - 21/3ak = 0 ( 0 < k < n ) かつ 21/3a0 ∈ Q
が成り立つ必要があります。(i) の場合、P(x) = a0x - 21/3a0 となり、21/3a0 ∈ Q ならば任意の q ∈ Q に対して a0 = q / 21/3 で q = 0 以外では a0 は無理数となるため条件を満たしません。q = 0 のとき P(x) = 0 なので、P(x) は x3 - 2 で割り切れることになります。
(ii) の場合、
ak-1 = 21/3ak より ak = 2-1/3a0
なので、
P(x) = 2-(n-1)/3a0xn - 21/3a0
となり、21/3a0 = q ∈ Q とすると a0 = 2-1/3q となります。このとき、
P(x) = 2-n/3qxn - q
なので、2-n/3q が有理数であるためには n = 3k ( k は 0 以上の整数 ) でなければなりません。k = 0 のときは n = 0 なので
P(x) = qx0 - q = 0
で成り立ちます。k ≥ 1 のときは
P(x)
= 2-kqx3k - q
= 2-kq( x3k - 2k )
= 2-kq( x3 - 2 )( x3(k-1) + 2x3(k-2) + ... + 2k-1 )
となるので、命題が成り立つことが証明されました。
予定より内容がふくらんでしまい、だいぶ時間がかかってしまいましたが何とか今年中に公開することができました。次のお題もだいたいは決まっているものの、どこで区切りを付けるか少々悩んでいます。まあ、今度はのんびりと進めることにします。
「数学問題 bot ( 個人用 )」から京大の問題を選んでみました。例によって合っている保証はありません。
-----
(1) 21/3 が無理数であることを示せ。
(2) P(x) は有理数を係数とする x の多項式で、P(21/3) = 0 を満たしているとする。このとき P(x) は x3 - 2 で割り切れることを証明せよ ( 2012 京大 )
(1) 21/3 = a / b ( 但し、a, b は互いに素な整数で b ≠ 0 とする ) と仮定します。この等式が成り立てば 21/3 は有理数です。このとき、両辺を 3 乗して
2 = a3 / b3 より a3 = 2b3
となり、a は 2 を素因数に持つことになります。a = 2c とすると、
8c3 = 2b3 より b3 = 4c3
となり、b は 2 を素因数に持つことになるので a, b が互いに素であるという仮定に反します。したがって、21/3 は有理数ではなく、無理数であることが証明されました。
(2) P(21/3) = 0 より P(x) は因数 x - 21/3 を持ちます。そこで
P(x) = ( x - 21/3 )Q(x)
Q(x) = Σk{0→n-1}( akxk )
とすると、
P(x)
= ( x - 21/3 )( an-1xn-1 + an-2xn-2 + ... + a0 )
= an-1xn + ( an-2 - 21/3an-1 )xn-1 + ... + ( a0 - 21/3a1 )x - 21/3a0
となります。P(x) の係数は有理数なので、Q を自然数全体の集合としたとき ak-1 - 21/3ak ∈ Q, an-1 ∈ Q, 21/3a0 ∈ Q が成り立つ必要があります。しかし、21/3 は無理数なので、
(i) ak = 0 ( 0 < k < n ) かつ 21/3a0 ∈ Q
または
(ii) ak-1 - 21/3ak = 0 ( 0 < k < n ) かつ 21/3a0 ∈ Q
が成り立つ必要があります。(i) の場合、P(x) = a0x - 21/3a0 となり、21/3a0 ∈ Q ならば任意の q ∈ Q に対して a0 = q / 21/3 で q = 0 以外では a0 は無理数となるため条件を満たしません。q = 0 のとき P(x) = 0 なので、P(x) は x3 - 2 で割り切れることになります。
(ii) の場合、
ak-1 = 21/3ak より ak = 2-1/3a0
なので、
P(x) = 2-(n-1)/3a0xn - 21/3a0
となり、21/3a0 = q ∈ Q とすると a0 = 2-1/3q となります。このとき、
P(x) = 2-n/3qxn - q
なので、2-n/3q が有理数であるためには n = 3k ( k は 0 以上の整数 ) でなければなりません。k = 0 のときは n = 0 なので
P(x) = qx0 - q = 0
で成り立ちます。k ≥ 1 のときは
P(x)
= 2-kqx3k - q
= 2-kq( x3k - 2k )
= 2-kq( x3 - 2 )( x3(k-1) + 2x3(k-2) + ... + 2k-1 )
となるので、命題が成り立つことが証明されました。





