2016年11月20日
コタツを出すにはまだ早いか?
11 月も半ばを過ぎて、もう今年も残り少なくなってきました。早いものです。
そろそろコタツの恋しい時期になってきました。昨日は雨が降っていたこともあって寒い一日でしたが、今日は比較的暖かくてコタツを出すには微妙ということでまだ出してはいません。部屋がそんなに広くはないのでコタツを出すと一気に場所が狭くなり、掃除するのも面倒になります。なので、いつも寒くてどうしようもなくなってきた年末ギリギリに出しています。今年も結局はそうなるかもしれません。
かなり前に、机の下に置いて利用できるタイプの小さなコタツを通販サイトで見つけたことがあります。足元さえ暖かければ上半身が冷えていてもさほど苦ではないので、いいのが見つかれば買ってみようかとも考えています。しかし家の机は木製で、しかも裏側は引き出しがむき出しの状態なので、裏側に取り付けるタイプのデスク・ヒーターは使えないんですよね。かなりモノが絞り込まれる気がします。
「数学問題 bot ( 個人用 )」からの出題です。例によって合っている保証はありません。
-----
4 つの正数 a, b, c, d について a = b = c = d でないならば、4 つの数 a( 1 - b ), b( 1 - c ), c( 1 - d ), d( 1 - a ) のうち少なくとも 1 つは 1 / 4 より小さいことを証明せよ ( 1978 年東京理科大 )
a, b, c, d のうち一つでも 1 以上ならば、4 つの数のうち少なくとも一つはゼロ以下になるので、a, b, c, d は 1 より小さい場合を考えればいいことになります。また、このとき 4 つの数が 1 / 4 以上になるためには ( a, b, c, d は 1 より小さいので ) 1 - a, 1 - b, 1 - c, 1 - d は 1 / 4 より大きくなければなりません。従って、a, b, c, d は 3 / 4 より小さいことになります。
今、a( 1 - b ), b( 1 - c ), c( 1 - d ) は全て 1 / 4 以上であると仮定します。このとき、
a( 1 - b ) ≥ 1 / 4 より 1 - a ≤ 1 - 1 / 4( 1 - b )
c( 1 - d ) ≥ 1 / 4 より d ≤ 1 - 1 / 4c = ( 4c - 1 ) / 4c
b( 1 - c ) ≥ 1 / 4 より 1 / 4( 1 - b ) ≥ ( 1 - c ) / [ 4( 1 - c ) - 1 ]
が成り立ちます。よって、
1 - a ≤ 1 - 1 / 4( 1 - b ) ≤ 1 - ( 1 - c ) / [ 4( 1 - c ) - 1 ] = ( 3c - 2 ) / ( 4c - 3 )
であり、これらの結果から
d( 1 - a ) ≤ ( 4c - 1 )( 3c - 2 ) / 4c( 4c - 3 )
となります。
f(c) = ( 4c - 1 )( 3c - 2 ) / 4c( 4c - 3 ) - 1 / 4 とすると、右辺を整理することで f(c) = ( 2c - 1 )2 / 2c( 4c - 3 ) となります。よって、c < 3 / 4 のとき f(c) ≤ 0 であり、等号は c = 1 / 2 のときに成り立ちます。
d( 1 - a ) = 1 / 4 のとき f(c) = 0 でなければならないので c = 1 / 2 になります。このとき b( 1 - c ) ≥ 1 / 4 より b ≥ 1 / 2 となります。また、c( 1 - d ) ≥ 1 / 4 より d ≤ 1 / 2 であり、d( 1 - a ) = 1 / 4 より a ≤ 1 / 2 です。よって、a( 1 - b ) ≥ 1 / 4 が成り立つためには a = b = 1 / 2 でなければならず、このとき d = 1 / 2 となります。従って、a = b = c = d でない場合は d( 1 - a ) ≤ 1 / 4 であり、対称性からどの三つの組み合わせを 1 / 4 以上にしても必ず一つは 1 / 4 より小さくなるので、命題が証明されました。
そろそろコタツの恋しい時期になってきました。昨日は雨が降っていたこともあって寒い一日でしたが、今日は比較的暖かくてコタツを出すには微妙ということでまだ出してはいません。部屋がそんなに広くはないのでコタツを出すと一気に場所が狭くなり、掃除するのも面倒になります。なので、いつも寒くてどうしようもなくなってきた年末ギリギリに出しています。今年も結局はそうなるかもしれません。
かなり前に、机の下に置いて利用できるタイプの小さなコタツを通販サイトで見つけたことがあります。足元さえ暖かければ上半身が冷えていてもさほど苦ではないので、いいのが見つかれば買ってみようかとも考えています。しかし家の机は木製で、しかも裏側は引き出しがむき出しの状態なので、裏側に取り付けるタイプのデスク・ヒーターは使えないんですよね。かなりモノが絞り込まれる気がします。
「数学問題 bot ( 個人用 )」からの出題です。例によって合っている保証はありません。
-----
4 つの正数 a, b, c, d について a = b = c = d でないならば、4 つの数 a( 1 - b ), b( 1 - c ), c( 1 - d ), d( 1 - a ) のうち少なくとも 1 つは 1 / 4 より小さいことを証明せよ ( 1978 年東京理科大 )
a, b, c, d のうち一つでも 1 以上ならば、4 つの数のうち少なくとも一つはゼロ以下になるので、a, b, c, d は 1 より小さい場合を考えればいいことになります。また、このとき 4 つの数が 1 / 4 以上になるためには ( a, b, c, d は 1 より小さいので ) 1 - a, 1 - b, 1 - c, 1 - d は 1 / 4 より大きくなければなりません。従って、a, b, c, d は 3 / 4 より小さいことになります。
今、a( 1 - b ), b( 1 - c ), c( 1 - d ) は全て 1 / 4 以上であると仮定します。このとき、
a( 1 - b ) ≥ 1 / 4 より 1 - a ≤ 1 - 1 / 4( 1 - b )
c( 1 - d ) ≥ 1 / 4 より d ≤ 1 - 1 / 4c = ( 4c - 1 ) / 4c
b( 1 - c ) ≥ 1 / 4 より 1 / 4( 1 - b ) ≥ ( 1 - c ) / [ 4( 1 - c ) - 1 ]
が成り立ちます。よって、
1 - a ≤ 1 - 1 / 4( 1 - b ) ≤ 1 - ( 1 - c ) / [ 4( 1 - c ) - 1 ] = ( 3c - 2 ) / ( 4c - 3 )
であり、これらの結果から
d( 1 - a ) ≤ ( 4c - 1 )( 3c - 2 ) / 4c( 4c - 3 )
となります。
f(c) = ( 4c - 1 )( 3c - 2 ) / 4c( 4c - 3 ) - 1 / 4 とすると、右辺を整理することで f(c) = ( 2c - 1 )2 / 2c( 4c - 3 ) となります。よって、c < 3 / 4 のとき f(c) ≤ 0 であり、等号は c = 1 / 2 のときに成り立ちます。
d( 1 - a ) = 1 / 4 のとき f(c) = 0 でなければならないので c = 1 / 2 になります。このとき b( 1 - c ) ≥ 1 / 4 より b ≥ 1 / 2 となります。また、c( 1 - d ) ≥ 1 / 4 より d ≤ 1 / 2 であり、d( 1 - a ) = 1 / 4 より a ≤ 1 / 2 です。よって、a( 1 - b ) ≥ 1 / 4 が成り立つためには a = b = 1 / 2 でなければならず、このとき d = 1 / 2 となります。従って、a = b = c = d でない場合は d( 1 - a ) ≤ 1 / 4 であり、対称性からどの三つの組み合わせを 1 / 4 以上にしても必ず一つは 1 / 4 より小さくなるので、命題が証明されました。
2016年10月23日
不等式の問題
「アルゴリズムのコーナー」の「画像処理」の章を全てリニューアルしました。主にサンプル・プログラムの見直しを行っています。
「シーム・カービング」は試してみて非常に楽しいアルゴリズムなので、時間があれば他にもいろいろと試してみたいです。また、そのうちに更新を行うかもしれませんが、当分は先の話になりそうです。まだ作ってみたいものは他にもたくさんありますし。
「数学問題bot」から不等式の問題です。最初は手も足も出ない状態でしたが、ふと思い立った方法でなんとか証明してみました。例によって合っている保証はありません。
-----
不等式 (1/2)・(3/4)・(5/6)・ ... ・(999999/1000000) < 1/1000 を示せ ( 第 14 回シュプリンガー数学コンテスト )
命題の証明の前に、二つの補題を証明しておきます。
(補題 1) ( 1 - 1 / n )-n は単調減少で lim{n→∞} ( 1 - 1 / n )-n = e
f(x) = ln ( 1 - 1 / x )-x ( x > 1 ) とすると、
f(x) = -x ln ( 1 - 1 / x ) = -x ln ( x - 1 ) + x ln x
f'(x) = -ln ( x - 1 ) - x / ( x - 1 ) + ln x + 1 = -ln ( x - 1 ) + ln x - 1 / ( x - 1 )
f''(x) = -1 / ( x - 1 ) + 1 / x + 1 / ( x - 1 )2
= [ -x( x - 1 ) + ( x - 1 )2 + x ] / x( x - 1 )2
= ( -x2 + x + x2 - 2x + 1 + x ) / x( x - 1 )2
= 1 / x( x - 1 )2 > 0
よって、f'(x) は単調増加です。また、
f'(x) = -ln ( x - 1 ) + ln x - 1 / ( x - 1 )
= ln ( 1 + 1 / ( x - 1 ) ) - 1 / ( x - 1 )
→ 0 ( x → ∞ )
なので f'(x) < 0 となり、f(x) は単調減少となることから ( 1 - 1 / n )-n も単調減少となります。
ネイピア数の定義より lim{n→∞} ( 1 + 1 / n )n = e であることを利用すると、
( 1 + 1 / n )n / ( 1 - 1 / n )-n
= ( 1 - 1 / n2 )n
= 1 - n( 1 / n2 ) + (1/2)n( n - 1 )( 1 / n2 )2 - ... + (-1)knCk( 1 / n2 )k + ... → 1 ( n → ∞ )
より lim{n→∞} ( 1 - 1 / n )-n = e となります。
(補題 2) 関数 ln x に対し、下図において A > B が常に成り立つ
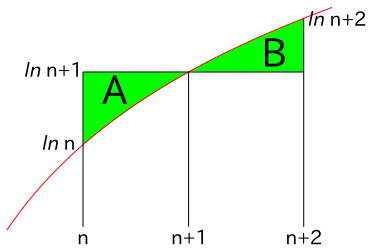
A = ln ( n + 1 ) - ∫{n→n+1} ln x dx
B = ∫{n+1→n+2} ln x dx - ln ( n + 1 )
より
A - B
= ln ( n + 1 ) - ∫{n→n+1} ln x dx - ∫{n+1→n+2} ln x dx + ln ( n + 1 )
= 2ln ( n + 1 ) - ∫{n→n+2} ln x dx
= 2ln ( n + 1 ) - [ x ln x ]{n→n+2} + [ x ]{n→n+2}
= 2ln ( n + 1 ) - ( n + 2 ) ln ( n + 2 ) + n ln n + 2
= ln ( n + 1 )2nne2 / ( n + 2 )n+2
= ln [ n / ( n + 2 ) ]n[ ( n + 1 ) / ( n + 2 ) ]2e2
となります。ここで
[ n / ( n + 2 ) ]n
= { [ 1 - 2 / ( n + 2 ) ](n+2)/2 }2[ ( n + 2 ) / n ]2
より
A - B = ln { [ 1 - 2 / ( n + 2 ) ](n+2)/2 }2[ ( n + 1 ) / n ]2e2
となり、補題 1 から { [ 1 - 2 / ( n + 2 ) ]-(n+2)/2 }2 は単調減少で → e2 ( n→∞ ) だから、{ [ 1 - 2 / ( n + 2 ) ](n+2)/2 }2 は単調増加で → 1 / e2 ( n→∞ ) となります。また、[ ( n + 1 ) / n ]2 → 1 ( n→∞ ) なので、A - B → ln ( 1 / e2 )・1・e2 = 0 ( n→∞ ) が成り立ちます。
n = 1 のとき、
A - B = ln ( 1 / 3 )( 2 / 3 )2e2 = ln ( 4 / 27 )e2 > ln ( 4 / 27 )( 2.7 )2 = ln 1.08 & gt; 0
なので、A - B が n の増加に対して単調減少であれば常に正であることになります。そこで、
f(x) = 2ln ( x + 1 ) - ( x + 2 ) ln ( x + 2 ) + x ln x + 2 ( x ≥ 1 )
とすると、
f'(x)
= 2 / ( x + 1 ) - ln ( x + 2 ) - 1 + ln x + 1
= 2 / ( x + 1 ) - ln ( x + 2 ) + ln x
f''(x)
= -2 / ( x + 1 )2 - 1 / ( x + 2 ) + 1 / x
= [ -2x( x + 2 ) - x( x + 1 )2 + ( x + 1 )2( x + 2 ) ] / x( x + 1 )2( x + 2 )
= [ -2x2 - 4x + 2( x + 1 )2 ] / x( x + 1 )2( x + 2 )
= 2 / x( x + 1 )2( x + 2 ) > 0
なので f'(x) は単調増加で、x = 1 のとき f'(1) = 1 - ln 3 > 0、f'(x) = 2 / ( x + 1 ) + ln ( 1 - 2 / ( x + 2 ) ) → 0 ( x→∞ ) だから、f'(x) < 0 が成り立ちます。よって f(x) は単調減少で、f(x) > 0 が常に成り立つことが証明されました。
(証明)
ln (1/2)・(3/4)・(5/6)・ ... ・(999999/1000000) = ( ln 1 + ln 3 + ... + ln 999999 ) - ( ln 2 + ln 4 + ... + ln 1000000 )
と変形できるので、左辺の二つの項についてその大きさを調べてみます。
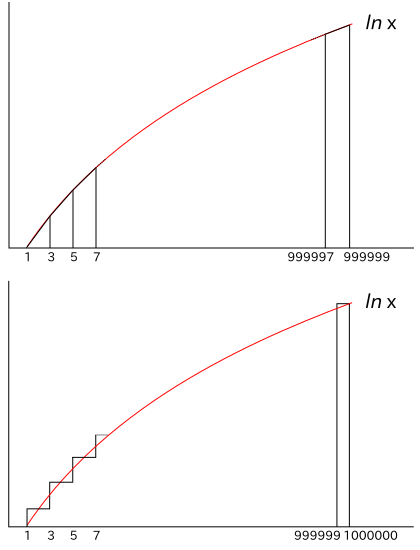
上図の上側の ln x と台形との面積の大きさを比較すると、
2( ln 1 + ln 3 ) / 2 + 2( ln 3 + ln 5 ) / 2 + ... 2( ln 999997 + ln 999999 ) / 2 < ∫{1→999999} ln x dx
が成り立ちます。この式は
ln1 + 2( ln 3 + ln 5 + ... + ln 999997 ) + ln 999999 < ∫{1→999999} ln x dx
と変形できて、ln 1 = 0 だから
ln1 + ln 3 + ln 5 + ... + ln 999997 + ln 999999 < (1/2)( ∫{1→999999} ln x dx + ln 999999 )
が成り立ちます。また、図の下側と補題 2 から
2 ln 2 + 2 ln 4 + 2 ln 6 + ... + ln 1000000 > ∫{1→1000000} ln x dx
なので、
ln 2 + ln 4 + ln 6 + ... + ln 1000000 > (1/2)( ∫{1→1000000} ln x dx + ln 1000000 )
となります。よって、
( ln 1 + ln 3 + ... + ln 999999 ) - ( ln 2 + ln 4 + ... + ln 1000000 ) < (1/2)( ∫{1→999999} ln x dx + ln 999999 - ∫{1→1000000} ln x dx + ln 1000000 )
ここで 1000000 = M, 999999 = m として右辺を変形すると
(右辺) = (1/2)[ ln ( m / M ) - ∫{m→M} ln x dx ]
∫{m→M} ln x dx
= [ x ln x ]{m→M} - &int{m→M} dx
= ln ( MM / mm ) - ( M - m )
= ln ( MM / mm ) - 1
よって
(右辺)
= (1/2)[ ln ( m / M ) - ln ( MM / mm ) + 1 )
= (1/2) ln ( mmme / MMM )
= (1/2) ln ( ( m / M )M( e / M ) )
= (1/2) ln ( ( 1 - 1 / M )M( e / M ) )
となります。補題 1 から
( 1 - 1 / M )M = 1 / ( 1 - 1 / M )-M → 1 / e ( M→∞ )
であり、( 1 - 1 / M )-M は単調減少だから ( 1 - 1 / M )-M > e より ( 1 - 1 / M )M < 1 / e となって、
( ln 1 + ln 3 + ... + ln 999999 ) - ( ln 2 + ln 4 + ... + ln 1000000 )
< (1/2)( ∫{1→999999} ln x dx + ln 999999 - ∫{1→1000000} ln x dx + ln 1000000 )
< (1/2)ln 1 / 1000000 = ln ( 1 / 1000 )
よって、不等式が証明されました。
「シーム・カービング」は試してみて非常に楽しいアルゴリズムなので、時間があれば他にもいろいろと試してみたいです。また、そのうちに更新を行うかもしれませんが、当分は先の話になりそうです。まだ作ってみたいものは他にもたくさんありますし。
「数学問題bot」から不等式の問題です。最初は手も足も出ない状態でしたが、ふと思い立った方法でなんとか証明してみました。例によって合っている保証はありません。
-----
不等式 (1/2)・(3/4)・(5/6)・ ... ・(999999/1000000) < 1/1000 を示せ ( 第 14 回シュプリンガー数学コンテスト )
命題の証明の前に、二つの補題を証明しておきます。
(補題 1) ( 1 - 1 / n )-n は単調減少で lim{n→∞} ( 1 - 1 / n )-n = e
f(x) = ln ( 1 - 1 / x )-x ( x > 1 ) とすると、
f(x) = -x ln ( 1 - 1 / x ) = -x ln ( x - 1 ) + x ln x
f'(x) = -ln ( x - 1 ) - x / ( x - 1 ) + ln x + 1 = -ln ( x - 1 ) + ln x - 1 / ( x - 1 )
f''(x) = -1 / ( x - 1 ) + 1 / x + 1 / ( x - 1 )2
= [ -x( x - 1 ) + ( x - 1 )2 + x ] / x( x - 1 )2
= ( -x2 + x + x2 - 2x + 1 + x ) / x( x - 1 )2
= 1 / x( x - 1 )2 > 0
よって、f'(x) は単調増加です。また、
f'(x) = -ln ( x - 1 ) + ln x - 1 / ( x - 1 )
= ln ( 1 + 1 / ( x - 1 ) ) - 1 / ( x - 1 )
→ 0 ( x → ∞ )
なので f'(x) < 0 となり、f(x) は単調減少となることから ( 1 - 1 / n )-n も単調減少となります。
ネイピア数の定義より lim{n→∞} ( 1 + 1 / n )n = e であることを利用すると、
( 1 + 1 / n )n / ( 1 - 1 / n )-n
= ( 1 - 1 / n2 )n
= 1 - n( 1 / n2 ) + (1/2)n( n - 1 )( 1 / n2 )2 - ... + (-1)knCk( 1 / n2 )k + ... → 1 ( n → ∞ )
より lim{n→∞} ( 1 - 1 / n )-n = e となります。
(補題 2) 関数 ln x に対し、下図において A > B が常に成り立つ

A = ln ( n + 1 ) - ∫{n→n+1} ln x dx
B = ∫{n+1→n+2} ln x dx - ln ( n + 1 )
より
A - B
= ln ( n + 1 ) - ∫{n→n+1} ln x dx - ∫{n+1→n+2} ln x dx + ln ( n + 1 )
= 2ln ( n + 1 ) - ∫{n→n+2} ln x dx
= 2ln ( n + 1 ) - [ x ln x ]{n→n+2} + [ x ]{n→n+2}
= 2ln ( n + 1 ) - ( n + 2 ) ln ( n + 2 ) + n ln n + 2
= ln ( n + 1 )2nne2 / ( n + 2 )n+2
= ln [ n / ( n + 2 ) ]n[ ( n + 1 ) / ( n + 2 ) ]2e2
となります。ここで
[ n / ( n + 2 ) ]n
= { [ 1 - 2 / ( n + 2 ) ](n+2)/2 }2[ ( n + 2 ) / n ]2
より
A - B = ln { [ 1 - 2 / ( n + 2 ) ](n+2)/2 }2[ ( n + 1 ) / n ]2e2
となり、補題 1 から { [ 1 - 2 / ( n + 2 ) ]-(n+2)/2 }2 は単調減少で → e2 ( n→∞ ) だから、{ [ 1 - 2 / ( n + 2 ) ](n+2)/2 }2 は単調増加で → 1 / e2 ( n→∞ ) となります。また、[ ( n + 1 ) / n ]2 → 1 ( n→∞ ) なので、A - B → ln ( 1 / e2 )・1・e2 = 0 ( n→∞ ) が成り立ちます。
n = 1 のとき、
A - B = ln ( 1 / 3 )( 2 / 3 )2e2 = ln ( 4 / 27 )e2 > ln ( 4 / 27 )( 2.7 )2 = ln 1.08 & gt; 0
なので、A - B が n の増加に対して単調減少であれば常に正であることになります。そこで、
f(x) = 2ln ( x + 1 ) - ( x + 2 ) ln ( x + 2 ) + x ln x + 2 ( x ≥ 1 )
とすると、
f'(x)
= 2 / ( x + 1 ) - ln ( x + 2 ) - 1 + ln x + 1
= 2 / ( x + 1 ) - ln ( x + 2 ) + ln x
f''(x)
= -2 / ( x + 1 )2 - 1 / ( x + 2 ) + 1 / x
= [ -2x( x + 2 ) - x( x + 1 )2 + ( x + 1 )2( x + 2 ) ] / x( x + 1 )2( x + 2 )
= [ -2x2 - 4x + 2( x + 1 )2 ] / x( x + 1 )2( x + 2 )
= 2 / x( x + 1 )2( x + 2 ) > 0
なので f'(x) は単調増加で、x = 1 のとき f'(1) = 1 - ln 3 > 0、f'(x) = 2 / ( x + 1 ) + ln ( 1 - 2 / ( x + 2 ) ) → 0 ( x→∞ ) だから、f'(x) < 0 が成り立ちます。よって f(x) は単調減少で、f(x) > 0 が常に成り立つことが証明されました。
(証明)
ln (1/2)・(3/4)・(5/6)・ ... ・(999999/1000000) = ( ln 1 + ln 3 + ... + ln 999999 ) - ( ln 2 + ln 4 + ... + ln 1000000 )
と変形できるので、左辺の二つの項についてその大きさを調べてみます。

上図の上側の ln x と台形との面積の大きさを比較すると、
2( ln 1 + ln 3 ) / 2 + 2( ln 3 + ln 5 ) / 2 + ... 2( ln 999997 + ln 999999 ) / 2 < ∫{1→999999} ln x dx
が成り立ちます。この式は
ln1 + 2( ln 3 + ln 5 + ... + ln 999997 ) + ln 999999 < ∫{1→999999} ln x dx
と変形できて、ln 1 = 0 だから
ln1 + ln 3 + ln 5 + ... + ln 999997 + ln 999999 < (1/2)( ∫{1→999999} ln x dx + ln 999999 )
が成り立ちます。また、図の下側と補題 2 から
2 ln 2 + 2 ln 4 + 2 ln 6 + ... + ln 1000000 > ∫{1→1000000} ln x dx
なので、
ln 2 + ln 4 + ln 6 + ... + ln 1000000 > (1/2)( ∫{1→1000000} ln x dx + ln 1000000 )
となります。よって、
( ln 1 + ln 3 + ... + ln 999999 ) - ( ln 2 + ln 4 + ... + ln 1000000 ) < (1/2)( ∫{1→999999} ln x dx + ln 999999 - ∫{1→1000000} ln x dx + ln 1000000 )
ここで 1000000 = M, 999999 = m として右辺を変形すると
(右辺) = (1/2)[ ln ( m / M ) - ∫{m→M} ln x dx ]
∫{m→M} ln x dx
= [ x ln x ]{m→M} - &int{m→M} dx
= ln ( MM / mm ) - ( M - m )
= ln ( MM / mm ) - 1
よって
(右辺)
= (1/2)[ ln ( m / M ) - ln ( MM / mm ) + 1 )
= (1/2) ln ( mmme / MMM )
= (1/2) ln ( ( m / M )M( e / M ) )
= (1/2) ln ( ( 1 - 1 / M )M( e / M ) )
となります。補題 1 から
( 1 - 1 / M )M = 1 / ( 1 - 1 / M )-M → 1 / e ( M→∞ )
であり、( 1 - 1 / M )-M は単調減少だから ( 1 - 1 / M )-M > e より ( 1 - 1 / M )M < 1 / e となって、
( ln 1 + ln 3 + ... + ln 999999 ) - ( ln 2 + ln 4 + ... + ln 1000000 )
< (1/2)( ∫{1→999999} ln x dx + ln 999999 - ∫{1→1000000} ln x dx + ln 1000000 )
< (1/2)ln 1 / 1000000 = ln ( 1 / 1000 )
よって、不等式が証明されました。
2016年10月16日
クラスタリング勉強中
少し前から、クラスタリングの勉強を始めてます。昔に覚えた手法も含めてもう一度基礎からやり直しで、ようやく少しずつ理解が進んできた感じです。で、SOM ( 自己組織化写像 ) のサンプル・プログラムを作成したのですが、思ったような結果が得られず苦戦しています。いつ頃公開できるかは未定ですが、とりあえず次のテーマはこのあたりにするつもりです。
数学問題bot から拾った問題です。例によって合っている保証はありません。
-----
n を 2 以上の整数とする。1 つのサイコロを n 回投げ、第 1 回目から第 n 回目までに出た目の最大公約数を G とする。G の期待値を n の式で表せ ( 07 大阪 )
サイコロを n 回投げたときの目の並べ方は 6n 通りあります。その中で G = 2 となるのは、目が 2, 4, 6 のいずれかで、全ての目が 4 のみまたは 6 のみの場合を除いたときなので、その並べ方は 3n - 2 通りになります。同様に、G = 3 となるのは目が 3, 6 のいずれかで、すべての目が 6 のみの場合を除いたときなのでその並べ方は 2n - 1 通りです。G = 4, 5, 6 になるのは、それぞれ目が 4, 5, 6 のみの場合だけなので各々 1 通りのみで、残りは G = 1 の場合で 6n - ( 3n - 2 ) - ( 2n - 1 ) - 3 = 6n - 3n - 2n 通りになります。従って G の期待値は
[ 2・( 3n - 2 ) + 3・( 2n - 1 ) + 4 + 5 + 6 + ( 6n - 3n - 2n ) ] / 6n
= ( 3n + 2n+1 + 6n + 8 ) / 6n
= ( 1 / 2 )n + 2( 1 / 3 )n + 8( 1 / 6 )n + 1
となります。n → ∞ のとき期待値が 1 に収束するのは、一回でも 1 の目が出れば G = 1 となることからも納得のできる結果です。
数学問題bot から拾った問題です。例によって合っている保証はありません。
-----
n を 2 以上の整数とする。1 つのサイコロを n 回投げ、第 1 回目から第 n 回目までに出た目の最大公約数を G とする。G の期待値を n の式で表せ ( 07 大阪 )
サイコロを n 回投げたときの目の並べ方は 6n 通りあります。その中で G = 2 となるのは、目が 2, 4, 6 のいずれかで、全ての目が 4 のみまたは 6 のみの場合を除いたときなので、その並べ方は 3n - 2 通りになります。同様に、G = 3 となるのは目が 3, 6 のいずれかで、すべての目が 6 のみの場合を除いたときなのでその並べ方は 2n - 1 通りです。G = 4, 5, 6 になるのは、それぞれ目が 4, 5, 6 のみの場合だけなので各々 1 通りのみで、残りは G = 1 の場合で 6n - ( 3n - 2 ) - ( 2n - 1 ) - 3 = 6n - 3n - 2n 通りになります。従って G の期待値は
[ 2・( 3n - 2 ) + 3・( 2n - 1 ) + 4 + 5 + 6 + ( 6n - 3n - 2n ) ] / 6n
= ( 3n + 2n+1 + 6n + 8 ) / 6n
= ( 1 / 2 )n + 2( 1 / 3 )n + 8( 1 / 6 )n + 1
となります。n → ∞ のとき期待値が 1 に収束するのは、一回でも 1 の目が出れば G = 1 となることからも納得のできる結果です。
2016年09月18日
夏の名残り
八月の中旬ごろに、ベランダでカミキリムシを見つけて写真に撮っていました。

昔はもっと頻繁に見る機会があったように思うのですが、自然が少なくなったのか、自分が自然から遠ざかってしまったのか。
最後にクワガタを見たのは何年前だったろうか。
「数学問題bot(個人用)」から東工大の問題にチャレンジ。合っている保証はありません ( かなり強引な解き方だと思います )。
-----
f(x) は周期は 2π の連続関数で、c は正の定数とする。すべての x について ∫{0→2π} f(t-x)sint dt = cf(x) が成り立つとき、f(x) および c の値を求めよ。ただし f(0) = 1 とする。( 東工大 1977 年誘導略 )
部分積分法により
∫{0→2π} f(t-x)sin t dt = -[ f(t-x)cos t ]{0→2π} + ∫{0→2π} f'(t-x)cos t dt
ここで、f(x) が周期 2π の連続関数なので f(2π-x)cos 2π = f(-x)cos 0 より [ f(t-x)cos t ]{0→2π} = 0 であり、
∫{0→2π} f(t-x)sin t dt = ∫{0→2π} f'(t-x)cos t dt
もう一度部分積分法を使って
∫{0→2π} f'(t-x)cos t dt
= [ f'(t-x)sin t ]{0→2π} - ∫{0→2π} f''(t-x)sin t dt
= -∫{0→2π} f''(t-x)sin t dt
よって、任意の x について ∫{0→2π} f(t-x)sin t dt = -∫{0→2π} f''(t-x)sin t dt となり、これが成り立つためには
f(x) = -f''(x)
でなければなりません。周期 2π の連続関数でこの条件を満たすものとして
f(x) = a sin( x - u ) + b cos( x - v )
があります。但し、a,b,u,v は任意の定数とします。このとき、f(0) = 1 より
-a sin u + b cos v = 1
が成り立ちます。
∫{0→2π} f(t-x)sin t dt
= ∫{0→2π} { a sin[ t - ( x + u ) ] + b cos[ t - ( x + v ) ] }sin t dt
= a∫{0→2π} [ sin t cos( x + u ) - cos t sin( x + u ) ]sin t dt
+ b∫{0→2π} [ cos t cos( x + v ) + sin t sin( x + v ) ]sin t dt
= [ a cos( x + u ) + b sin( x + v ) ]∫{0→2π} sin2t dt
- [ a sin( x + u ) - b cos( x + v ) ]∫{0→2π} sin t cos t dt
sin 2t = 2 sin t cos t より
∫{0→2π} sin t cos t dt
= (1/2)∫{0→2π} sin 2t dt
= (1/4)[ -cos 2t ]{0→2π} = 0
なので二項目は消え、
cos 2t = cos2t - sin2t = 1 - 2sin2t より
∫{0→2π} sin2t dt
= (1/2)∫{0→2π} 1 - cos 2t dt
= (1/2)[ t - (1/2)sin 2t ]{0→2π} = π
よって、
∫{0→2π} f(t-x)sin t dt = π[ a cos( x + u ) + b sin( x + v ) ]
となります。また、
c f(x) = c[ a sin( x - u ) + b cos( x - v ) ]
より、
π[ a cos( x + u ) + b sin( x + v ) ] = c[ a sin( x - u ) + b cos( x - v ) ]
を満たす定数を求めれば、c と f(x) を得ることができます。
(左辺)
= π[ a( cos x cos u - sin x sin u ) + b( sin x cos v + cos x sin v ) ]
= π[ ( -a sin u + b cos v )sin x + ( a cos u + b sin v )cos x ]
ここで、-a sin u + b cos v = 1 より
= π[ sin x + ( a cos u + b sin v )cos x ]
(右辺)
= c[ a( sin x cos u - cos x sin u ) + b( cos x cos v + sin x sin v ) ]
= c[ ( a cos u + b sin v )sin x + ( -a sin u + b cos v )cos x ]
= c[ ( a cos u + b sin v )sin x + cos x ]
恒等的に (左辺) = (右辺) が成り立つためには
c( a cos u + b sin v ) = π
c = π( a cos u + b sin v )
よって
c2 = π2
より c > 0 なので c = π となり、
a cos u + b sin v = 1
となります。従って、
f(x) = sin x + cos x
c = π
が求める解となります。

昔はもっと頻繁に見る機会があったように思うのですが、自然が少なくなったのか、自分が自然から遠ざかってしまったのか。
最後にクワガタを見たのは何年前だったろうか。
「数学問題bot(個人用)」から東工大の問題にチャレンジ。合っている保証はありません ( かなり強引な解き方だと思います )。
-----
f(x) は周期は 2π の連続関数で、c は正の定数とする。すべての x について ∫{0→2π} f(t-x)sint dt = cf(x) が成り立つとき、f(x) および c の値を求めよ。ただし f(0) = 1 とする。( 東工大 1977 年誘導略 )
部分積分法により
∫{0→2π} f(t-x)sin t dt = -[ f(t-x)cos t ]{0→2π} + ∫{0→2π} f'(t-x)cos t dt
ここで、f(x) が周期 2π の連続関数なので f(2π-x)cos 2π = f(-x)cos 0 より [ f(t-x)cos t ]{0→2π} = 0 であり、
∫{0→2π} f(t-x)sin t dt = ∫{0→2π} f'(t-x)cos t dt
もう一度部分積分法を使って
∫{0→2π} f'(t-x)cos t dt
= [ f'(t-x)sin t ]{0→2π} - ∫{0→2π} f''(t-x)sin t dt
= -∫{0→2π} f''(t-x)sin t dt
よって、任意の x について ∫{0→2π} f(t-x)sin t dt = -∫{0→2π} f''(t-x)sin t dt となり、これが成り立つためには
f(x) = -f''(x)
でなければなりません。周期 2π の連続関数でこの条件を満たすものとして
f(x) = a sin( x - u ) + b cos( x - v )
があります。但し、a,b,u,v は任意の定数とします。このとき、f(0) = 1 より
-a sin u + b cos v = 1
が成り立ちます。
∫{0→2π} f(t-x)sin t dt
= ∫{0→2π} { a sin[ t - ( x + u ) ] + b cos[ t - ( x + v ) ] }sin t dt
= a∫{0→2π} [ sin t cos( x + u ) - cos t sin( x + u ) ]sin t dt
+ b∫{0→2π} [ cos t cos( x + v ) + sin t sin( x + v ) ]sin t dt
= [ a cos( x + u ) + b sin( x + v ) ]∫{0→2π} sin2t dt
- [ a sin( x + u ) - b cos( x + v ) ]∫{0→2π} sin t cos t dt
sin 2t = 2 sin t cos t より
∫{0→2π} sin t cos t dt
= (1/2)∫{0→2π} sin 2t dt
= (1/4)[ -cos 2t ]{0→2π} = 0
なので二項目は消え、
cos 2t = cos2t - sin2t = 1 - 2sin2t より
∫{0→2π} sin2t dt
= (1/2)∫{0→2π} 1 - cos 2t dt
= (1/2)[ t - (1/2)sin 2t ]{0→2π} = π
よって、
∫{0→2π} f(t-x)sin t dt = π[ a cos( x + u ) + b sin( x + v ) ]
となります。また、
c f(x) = c[ a sin( x - u ) + b cos( x - v ) ]
より、
π[ a cos( x + u ) + b sin( x + v ) ] = c[ a sin( x - u ) + b cos( x - v ) ]
を満たす定数を求めれば、c と f(x) を得ることができます。
(左辺)
= π[ a( cos x cos u - sin x sin u ) + b( sin x cos v + cos x sin v ) ]
= π[ ( -a sin u + b cos v )sin x + ( a cos u + b sin v )cos x ]
ここで、-a sin u + b cos v = 1 より
= π[ sin x + ( a cos u + b sin v )cos x ]
(右辺)
= c[ a( sin x cos u - cos x sin u ) + b( cos x cos v + sin x sin v ) ]
= c[ ( a cos u + b sin v )sin x + ( -a sin u + b cos v )cos x ]
= c[ ( a cos u + b sin v )sin x + cos x ]
恒等的に (左辺) = (右辺) が成り立つためには
c( a cos u + b sin v ) = π
c = π( a cos u + b sin v )
よって
c2 = π2
より c > 0 なので c = π となり、
a cos u + b sin v = 1
となります。従って、
f(x) = sin x + cos x
c = π
が求める解となります。
2016年08月14日
盆休み
お盆休みに入りましたが、相変わらず蒸し暑い日が続きます。明日は雨のようですね。さらに湿度が上がりそうな予感が。。。
「数学問題bot(個人用)」から東大の問題を解いてみました。例によって合っている保証はありません。
-----
0 ≤ n ≤ m を満たすすべての整数 n について、mCn が奇数となる m を求めよ ( 1999年東大 )
mCn については以下の定理が成り立ちます。
mC0 = 1
mC1 = m
m+1Cn = mCn-1 + mCn
mCn = mCm-n
3 番目はいわゆる「パスカルの三角形」で、mCn を m = 0 を一番上にして下へ順番に、n = 0 を一番左側にして右の方へ順番に並べると以下の様な三角形ができます。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
:
実際は正三角形の形に表しますが、面倒なので上のような書き方にしています。頂上から順に、x, x + y, ( x + y )2 ... を展開したときの係数と等しく、上側の二つの値を足すと下側の値になります。また、左右対称の形になっているのは先に示した 4 番目の式を表します。
パスカルの三角形を見ると、すでに m = 0, 1, 3, 7 のときに各係数は奇数となっているので、この結果から m = 2k - 1 ( k > 0 ) が解答であることが予想できます。そこで、2k-1-1Cn について命題が成り立つと仮定すると、
2k-1Cn
= ( 2k - 1 )! / ( 2k - n - 1 )!n!
= ( 2k - 1 )( 2k - 2 )...2k-1( 2k-1 - 1 )! / ( 2k - n - 1 )( 2k - n - 2 )...( 2k-1 - n )( 2k-1 - n - 1 )!n!
= [ ( 2k - 1 )( 2k - 2 )...2k-1 / ( 2k - n - 1 )( 2k - n - 2 )...( 2k-1 - n ) ]2k-1-1Cn
となるので、
kLn = ( 2k - 1 )( 2k - 2 )...2k-1 / ( 2k - n - 1 )( 2k - n - 2 )...( 2k-1 - n )
として、kLn が奇数であることを証明します。まず、明らかに kL0 = 1 です。また、分子の第一項は奇数であり、最後の項は偶数で、分子・分母ともに 2k-1 個の項の積となっています。分子は
( 2k - 1 )( 2k - 2 )...2k-1
= ( 2k - 1 )・2( 2k-1 - 1 )・( 2k - 3 )・22( 2k-2 - 1 )...2k-1
= 2k(k-1)/2(odd) ( 但し (odd) は奇数 )
で表せます。従って、分母に対しても 2 が k( k - 1 ) / 2 個あることが示されれば kLn は奇数であることになります。まず、n = 0 のときは分子・分母はともに等しくなるので成り立ちます。そこで、n のときに成り立っていると仮定します。このとき、n = 0 の場合に対して前側の項は n 個分少なくなり、同時に末尾には n 個の項が増えた形になります。n が奇数なら先頭は偶数、末尾は奇数であり、n が偶数ならその逆で、偶奇は交互に現れます。
n + 1 のときは、先頭の項がなくなり、末尾に項が一つ増えます。n が偶数のときは奇数の項が増減するだけなので 2 のべき数は変化しません。n が奇数のとき、2k - n - 1 がなくなり、2k-1 - n - 1 が増えます。n + 1 は偶数なので、これを 2pq ( 但し q は奇数 ) とすると、
2k - n - 1 = 2k - 2pq = 2p( 2k-p - q )
2k-1 - n - 1 = 2k-1 - 2pq = 2p( 2k-p-1 - q )
なのでやはり 2 のべき数は変わりません。
よって、帰納法により kLn は奇数であることになり、命題が証明されました。
係数を偶数は . 奇数は o としてパスカルの三角形を書くと以下のようになります。

この模様はさらに下側の三角形にも現れ、それが永遠に続きます。いわゆるフラクタル図形で「シェルピンスキーのガスケット」と呼ばれます。
「数学問題bot(個人用)」から東大の問題を解いてみました。例によって合っている保証はありません。
-----
0 ≤ n ≤ m を満たすすべての整数 n について、mCn が奇数となる m を求めよ ( 1999年東大 )
mCn については以下の定理が成り立ちます。
mC0 = 1
mC1 = m
m+1Cn = mCn-1 + mCn
mCn = mCm-n
3 番目はいわゆる「パスカルの三角形」で、mCn を m = 0 を一番上にして下へ順番に、n = 0 を一番左側にして右の方へ順番に並べると以下の様な三角形ができます。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
:
実際は正三角形の形に表しますが、面倒なので上のような書き方にしています。頂上から順に、x, x + y, ( x + y )2 ... を展開したときの係数と等しく、上側の二つの値を足すと下側の値になります。また、左右対称の形になっているのは先に示した 4 番目の式を表します。
パスカルの三角形を見ると、すでに m = 0, 1, 3, 7 のときに各係数は奇数となっているので、この結果から m = 2k - 1 ( k > 0 ) が解答であることが予想できます。そこで、2k-1-1Cn について命題が成り立つと仮定すると、
2k-1Cn
= ( 2k - 1 )! / ( 2k - n - 1 )!n!
= ( 2k - 1 )( 2k - 2 )...2k-1( 2k-1 - 1 )! / ( 2k - n - 1 )( 2k - n - 2 )...( 2k-1 - n )( 2k-1 - n - 1 )!n!
= [ ( 2k - 1 )( 2k - 2 )...2k-1 / ( 2k - n - 1 )( 2k - n - 2 )...( 2k-1 - n ) ]2k-1-1Cn
となるので、
kLn = ( 2k - 1 )( 2k - 2 )...2k-1 / ( 2k - n - 1 )( 2k - n - 2 )...( 2k-1 - n )
として、kLn が奇数であることを証明します。まず、明らかに kL0 = 1 です。また、分子の第一項は奇数であり、最後の項は偶数で、分子・分母ともに 2k-1 個の項の積となっています。分子は
( 2k - 1 )( 2k - 2 )...2k-1
= ( 2k - 1 )・2( 2k-1 - 1 )・( 2k - 3 )・22( 2k-2 - 1 )...2k-1
= 2k(k-1)/2(odd) ( 但し (odd) は奇数 )
で表せます。従って、分母に対しても 2 が k( k - 1 ) / 2 個あることが示されれば kLn は奇数であることになります。まず、n = 0 のときは分子・分母はともに等しくなるので成り立ちます。そこで、n のときに成り立っていると仮定します。このとき、n = 0 の場合に対して前側の項は n 個分少なくなり、同時に末尾には n 個の項が増えた形になります。n が奇数なら先頭は偶数、末尾は奇数であり、n が偶数ならその逆で、偶奇は交互に現れます。
| ( 2k - n - 1 ) | ( 2k - n - 2 ) | ... | ( 2k-1 - n ) | |
| n が奇数 | 偶 | 奇 | 奇 | |
| n が偶数 | 奇 | 偶 | 偶 |
n + 1 のときは、先頭の項がなくなり、末尾に項が一つ増えます。n が偶数のときは奇数の項が増減するだけなので 2 のべき数は変化しません。n が奇数のとき、2k - n - 1 がなくなり、2k-1 - n - 1 が増えます。n + 1 は偶数なので、これを 2pq ( 但し q は奇数 ) とすると、
2k - n - 1 = 2k - 2pq = 2p( 2k-p - q )
2k-1 - n - 1 = 2k-1 - 2pq = 2p( 2k-p-1 - q )
なのでやはり 2 のべき数は変わりません。
よって、帰納法により kLn は奇数であることになり、命題が証明されました。
係数を偶数は . 奇数は o としてパスカルの三角形を書くと以下のようになります。

この模様はさらに下側の三角形にも現れ、それが永遠に続きます。いわゆるフラクタル図形で「シェルピンスキーのガスケット」と呼ばれます。
2016年06月19日
ピカ・パウ
昨日は、いっしょに演奏しているグループのメンバーと静岡に遊びに行ってました。
沼津で海鮮づくしのあと、三島市にある「ピカ・パウ」という店で他のグループの方といっしょに夕食 + 演奏で楽しんできました。昼間は異常な暑さでしたが、駿河湾のクルージングで外洋に出ると結構涼しい風が吹いていて心地よかったです。
ピカ・パウは南米料理の専門店。昼間の海鮮づくしでお腹が空いておらずあまり食べられませんでしたが、料理はおいしかったですよ。大半はビール飲みながら演奏してたので、今度は食事目当てで行ってみたいです。
ピカ・パウ ( Pica Pau ) の意味を調べてみましたが、Google 翻訳はダメでした。ググってみるとアニメの Woodpecker がでてくるので、キツツキを意味するんでしょうかね?
「数学問題 bot」さんから、東大の出題問題です。合っている保証はありません。
-----
10進法で表して5桁以上の平方数に対し、1000の位の数、100の位の数、10の位の数、および1の位の数の4つ全てが同じ数となるならば、その平方数は10000で割り切れることを示せ。 ( 04 東大理系 )
1000 の位までの数が決まるのは、元の数の 2 桁分のみです。なぜなら、3 桁目は 100n で表せるので、平方すれば 10000n2 で、下 4 桁に影響しないからです。従って、01 ~ 99 の中で、平方して 4 桁が等しくなるような数が存在しなければ、ゼロ以外に条件を満たす数は存在しないことになります。
平方数の下一桁は、1 の位の数の平方の下一桁のみで決まるので、1, 4, 5, 6, 9 のいずれかしかありません。よって、平方して 4 つの数が同じになる場合は 1111, 4444, 5555, 6666, 9999 の 5 つに絞られます。
1111 = 11 x 101 なので、これは成り立ちません。同様に
4444 = 22 x 11 x 101
5555 = 5 x 11 x 101
6666 = 2 x 3 x 11 x 101
9999 = 32 x 11 x 101
であり、いずれも平方数にはならないので、ゼロ以外に条件を満たす数は存在せず、平方数は必ず 10000 で割り切れることが証明されました。
沼津で海鮮づくしのあと、三島市にある「ピカ・パウ」という店で他のグループの方といっしょに夕食 + 演奏で楽しんできました。昼間は異常な暑さでしたが、駿河湾のクルージングで外洋に出ると結構涼しい風が吹いていて心地よかったです。
ピカ・パウは南米料理の専門店。昼間の海鮮づくしでお腹が空いておらずあまり食べられませんでしたが、料理はおいしかったですよ。大半はビール飲みながら演奏してたので、今度は食事目当てで行ってみたいです。
ピカ・パウ ( Pica Pau ) の意味を調べてみましたが、Google 翻訳はダメでした。ググってみるとアニメの Woodpecker がでてくるので、キツツキを意味するんでしょうかね?
「数学問題 bot」さんから、東大の出題問題です。合っている保証はありません。
-----
10進法で表して5桁以上の平方数に対し、1000の位の数、100の位の数、10の位の数、および1の位の数の4つ全てが同じ数となるならば、その平方数は10000で割り切れることを示せ。 ( 04 東大理系 )
1000 の位までの数が決まるのは、元の数の 2 桁分のみです。なぜなら、3 桁目は 100n で表せるので、平方すれば 10000n2 で、下 4 桁に影響しないからです。従って、01 ~ 99 の中で、平方して 4 桁が等しくなるような数が存在しなければ、ゼロ以外に条件を満たす数は存在しないことになります。
平方数の下一桁は、1 の位の数の平方の下一桁のみで決まるので、1, 4, 5, 6, 9 のいずれかしかありません。よって、平方して 4 つの数が同じになる場合は 1111, 4444, 5555, 6666, 9999 の 5 つに絞られます。
1111 = 11 x 101 なので、これは成り立ちません。同様に
4444 = 22 x 11 x 101
5555 = 5 x 11 x 101
6666 = 2 x 3 x 11 x 101
9999 = 32 x 11 x 101
であり、いずれも平方数にはならないので、ゼロ以外に条件を満たす数は存在せず、平方数は必ず 10000 で割り切れることが証明されました。
2016年06月04日
梅雨入り
とうとう、梅雨入り宣言されました。
来週は晴れの日はほとんどないようです。しかし、大雨にならなければそれほど苦にもならないというものです。ゲリラ豪雨だけはかんべんしてほしいですね。
「数学問題bot」さんから今回は京大の問題。解き方を気付いた後は割と簡単に解けました。気付くまでが大変ですが。
例によって合っている保証なしです。
-----
2 以上の自然数 n に対し、n と n2 + 2 がともに素数になるのは n = 3 の場合に限ることを示せ。( 06 京都前期・理 )
全ての自然数は、k ≥ 0 として 3k, 3k + 1, 3k + 2 で表すことができます。3k は k & gt; 1 のとき合成数なので、n = 3k + 1, 3k + 2 として n2 + 2 を計算すると
( 3k + 1 )2 + 2 = 9k2 + 6k + 3 = 3( 3k2 + 2k + 1 )
( 3k + 2 )2 + 2 = 9k2 + 12k + 6 = 3( 3k2 + 4k + 2 )
で必ず 3 の倍数になります。従って、n と n2 + 2 が n = 3 以外でともに素数となることはありません。
来週は晴れの日はほとんどないようです。しかし、大雨にならなければそれほど苦にもならないというものです。ゲリラ豪雨だけはかんべんしてほしいですね。
「数学問題bot」さんから今回は京大の問題。解き方を気付いた後は割と簡単に解けました。気付くまでが大変ですが。
例によって合っている保証なしです。
-----
2 以上の自然数 n に対し、n と n2 + 2 がともに素数になるのは n = 3 の場合に限ることを示せ。( 06 京都前期・理 )
全ての自然数は、k ≥ 0 として 3k, 3k + 1, 3k + 2 で表すことができます。3k は k & gt; 1 のとき合成数なので、n = 3k + 1, 3k + 2 として n2 + 2 を計算すると
( 3k + 1 )2 + 2 = 9k2 + 6k + 3 = 3( 3k2 + 2k + 1 )
( 3k + 2 )2 + 2 = 9k2 + 12k + 6 = 3( 3k2 + 4k + 2 )
で必ず 3 の倍数になります。従って、n と n2 + 2 が n = 3 以外でともに素数となることはありません。
2016年05月28日
現在、湿度 60%
だんだんと湿度が上がってきて蒸し暑い日が続くようになりました。もうすぐ梅雨が始まりますね。
少し前ですが、「アルゴリズムのコーナー」を更新しました。今回も新規ではなく内容の見直しになります。
「算術符号化」
「EBCOTとMQ-Coder」
「EBCOTとMQ-Coder」はほぼ全てのサンプル・プログラムをページに載せたので、分量が多くなってしまいました。
次回は何にするか、少々悩んでます。新たなネタが一つあって現在まとめ中ですが、まだ理解不足のところが多々あり時間がかかりそうです。その間に過去の内容の見直しをするかもしれません。
さて、「数学問題bot」さんから拾った問題です。かなり悩みました ( 特に 2 番)。例によって合っている保証はありません。
-----
1) 3n = k3 + 1 をみたす正の整数の組 ( k, n ) を全て求めよ。
2) 3n = k2 - 40 をみたす正の整数の組 ( k, n ) を全て求めよ。( 10 千葉 )
1)
k3 + 1 = ( k + 1 )3 - 3k( k + 1 ) より
3n + 3k( k + 1 ) = ( k + 1 )3
を満たす ( k, n ) の組を見つければいいことになります。n > 0 より
3・[ 3n-1 + k( k + 1 ) ] = ( k + 1 )3
となるので k + 1 は 3 の倍数であり、k + 1 = 3m とすれば
3・[ 3n-1 + 3m( 3m - 1 ) ] = ( 3m )3 = 27m3
となり、両辺を 3 で割って
3n-1 + 3m( 3m - 1 ) = 9m3
となります。式を変形して
3n-1 = 3m・[ 3m2 - ( 3m - 1 ) ]
なので、右辺は 3 のみを素因数として持たねばなりません。
m = 1 のとき、(右辺) = 3 で、( k, n ) = ( 2, 2 ) が該当します。
m > 1 のとき、m は 3 のべき乗でなければなりませんが、そうすると
3m2 - ( 3m - 1 ) = 3m( m - 1 ) + 1
は 3 の倍数になりません。
従って、( k, n ) = ( 2, 2 ) のみが該当することになります。
2)
k2 = 3n + 40 として n = 1 の場合から実際に計算してみます。
まず、n が奇数の時に着目すると、k2 の下一桁めは 3 か 7 のいずれかになります。n = 1 のとき 3n = 3 であり、40 を加えても下一桁は変わりません。n = 3 では 9 を掛けることになり 3n = 27 ≡ 7 ( mod 10 ) です。n = 5 ではまた 9 を掛けることになるので 3n = 243 ≡ 3 ( mod 10 ) で、以下 3 と 7 を繰り返すことになります。ところで、二乗数の下一桁は、計算すればすぐわかるように 1, 4, 5, 6, 9 のいずれかしか現れません。従って、n が奇数のときは二乗数になり得ないことになります。
n が偶数のとき、n = 4 までは k が得られていますが、それ以降は新たな k は見つかっていません。n が偶数ならば、3n は必ず二乗数になります。例えば n = 6 のとき、3n = 272 であり、これにある数を加えて二乗数にしたいとき、次の数は 282 なので、その差は
282 - 272 = ( 28 + 27 )( 28 - 27 ) = 55 > 40
となります。従って、40 を加えても二乗数にすることができません。n = 6 以降の全てに対してそうなので、これ以上は見つからないことを意味します。
よって、得られる組は ( k, n ) = ( 7, 2 ), ( 11, 4 ) の二つです。
少し前ですが、「アルゴリズムのコーナー」を更新しました。今回も新規ではなく内容の見直しになります。
「算術符号化」
「EBCOTとMQ-Coder」
「EBCOTとMQ-Coder」はほぼ全てのサンプル・プログラムをページに載せたので、分量が多くなってしまいました。
次回は何にするか、少々悩んでます。新たなネタが一つあって現在まとめ中ですが、まだ理解不足のところが多々あり時間がかかりそうです。その間に過去の内容の見直しをするかもしれません。
さて、「数学問題bot」さんから拾った問題です。かなり悩みました ( 特に 2 番)。例によって合っている保証はありません。
-----
1) 3n = k3 + 1 をみたす正の整数の組 ( k, n ) を全て求めよ。
2) 3n = k2 - 40 をみたす正の整数の組 ( k, n ) を全て求めよ。( 10 千葉 )
1)
k3 + 1 = ( k + 1 )3 - 3k( k + 1 ) より
3n + 3k( k + 1 ) = ( k + 1 )3
を満たす ( k, n ) の組を見つければいいことになります。n > 0 より
3・[ 3n-1 + k( k + 1 ) ] = ( k + 1 )3
となるので k + 1 は 3 の倍数であり、k + 1 = 3m とすれば
3・[ 3n-1 + 3m( 3m - 1 ) ] = ( 3m )3 = 27m3
となり、両辺を 3 で割って
3n-1 + 3m( 3m - 1 ) = 9m3
となります。式を変形して
3n-1 = 3m・[ 3m2 - ( 3m - 1 ) ]
なので、右辺は 3 のみを素因数として持たねばなりません。
m = 1 のとき、(右辺) = 3 で、( k, n ) = ( 2, 2 ) が該当します。
m > 1 のとき、m は 3 のべき乗でなければなりませんが、そうすると
3m2 - ( 3m - 1 ) = 3m( m - 1 ) + 1
は 3 の倍数になりません。
従って、( k, n ) = ( 2, 2 ) のみが該当することになります。
2)
k2 = 3n + 40 として n = 1 の場合から実際に計算してみます。
| n | k2 | k |
|---|---|---|
| 1 | 43 | - |
| 2 | 49 | 7 |
| 3 | 67 | - |
| 4 | 121 | 11 |
| 5 | 283 | - |
| 6 | 769 | - |
| 7 | 2227 | - |
| 8 | 6601 | - |
まず、n が奇数の時に着目すると、k2 の下一桁めは 3 か 7 のいずれかになります。n = 1 のとき 3n = 3 であり、40 を加えても下一桁は変わりません。n = 3 では 9 を掛けることになり 3n = 27 ≡ 7 ( mod 10 ) です。n = 5 ではまた 9 を掛けることになるので 3n = 243 ≡ 3 ( mod 10 ) で、以下 3 と 7 を繰り返すことになります。ところで、二乗数の下一桁は、計算すればすぐわかるように 1, 4, 5, 6, 9 のいずれかしか現れません。従って、n が奇数のときは二乗数になり得ないことになります。
n が偶数のとき、n = 4 までは k が得られていますが、それ以降は新たな k は見つかっていません。n が偶数ならば、3n は必ず二乗数になります。例えば n = 6 のとき、3n = 272 であり、これにある数を加えて二乗数にしたいとき、次の数は 282 なので、その差は
282 - 272 = ( 28 + 27 )( 28 - 27 ) = 55 > 40
となります。従って、40 を加えても二乗数にすることができません。n = 6 以降の全てに対してそうなので、これ以上は見つからないことを意味します。
よって、得られる組は ( k, n ) = ( 7, 2 ), ( 11, 4 ) の二つです。
2016年05月13日
13日の金曜日
今日は「13日の金曜日」です。
イエスが磔刑にされたのが云々というのはウソのようで、はっきりしたことはわかってないみたいですね。中世の頃から始まった迷信だそうですが、日本ではやはりあの映画から有名になったのではないでしょうか。一作目は面白かったと思います。二作目以降も見たような気もしますがほとんど覚えてません。ジェイソンが首吊り状態になっても自力でほどいてしまうシーンを覚えているんですけど、あれは何作目だったんでしょうかね。
今回は「マテマティカ 2」さんから拾った問題です。かなり苦戦した上に、合っているかどうか自信は全くありません。せっかく解いたので載せておきます。
-----
二次正方行列 A, B が次の二条件を満たしている。
(i) A - B = AB
(ii) ( A + B )n = 0 となる正の整数 n が存在する
このとき、B を A と E の一次式で表わせ。
まず、次の命題を証明します。
二次行列 A が逆行列を持たないとき、An = [ tr(A) ]n-1A
但し、tr(A) は A の対角成分の和とする。
とします。このとき、
となりますが、A が逆行列を持たないとき ad - bc = 0 なので、ad = bc より
となります。
An = (a+d)n-1A が成り立つと仮定します。このとき
= (a+d)nA
なので、帰納法により命題が証明されました。
An = 0 のとき、A が逆行列を持てばそれを n - 1 回掛けることで A = 0 となり、0 は逆行列を持たないので矛盾します。従って、A ≠ 0 のとき、An = 0 が成り立つならば、A は逆行列を持ちません。このとき、An = (a+d)n-1A = 0 が成り立つので、a + d = 0 かつ |A| = 0 であることになります。A2 = (a+d)A なので、An = 0 となる n が存在するならばその最小値は 1 か 2 のいずれかであることになります ( n = 1 ならば A = 0 です )。
( A + B )n = 0 が成り立つとき、
とすれば
a + e + d + h = 0 --- (1)
| A + B | = ( a + e )( d + h ) - ( b + f )( c + g ) = 0 --- (2)
が成り立ちます。B = pA + qE ( 但し p ≠ 0 ) とすると、
なので、(1) より
a + ( pa + q ) + d + ( pd + q ) = ( p + 1 )( a + d ) + 2q = 0 --- (1')
であり、(2) より
[ a + ( pa + q ) ][ d + ( pd + q ) ] - ( b + pb )( c + pc )
= [ ( p + 1 )a + q ][ ( p + 1 )d + q ] - ( p + 1 )2bc
= ( p + 1 )2( ad - bc ) + q( p + 1 )( a + d ) + q2 = 0 --- (2')
になります。
(1') を (2') に代入して整理すると、
( p + 1 )2|A| = q2 --- (3)
となります。次に、
A - B = ( 1 - p )A - qE
AB = pA2 + qA
なので、A - B = AB ならば
( 1 - p )A - qE = pA2 + qA
となります。これを整理すると
A2 - [ ( 1 - p - q ) / p ]A + ( q / p )E = 0
となりますが、ケーリー・ハミルトンの公式から
( 1 - p - q ) / p = a + d --- (4)
q / p = |A| --- (5)
が成り立つ必要があります。従って、(3),(5) から
q2 / ( p + 1 )2 = q / p ( 但し p ≠ -1 とする ) より
q = ( p + 1 )2 / p --- (6)
となり、(5) に代入して
|A| = [ ( p + 1 ) / p ]2 --- (7)
(4) に代入して
{ 1 - p - [ ( p + 1 )2 / p ] } / p
= [ p - p2 - ( p2 + 2p + 1 ) ] / p2
= -( 2p2 + p + 1 ) / p2 = a + d --- (8)
となります。(7)(8) を満たす p が存在するとき、(6) によって q が決定し、B の一次式も決まります。
p = -1 のとき、(3) より q = 0 なので (6) を満たします。B = -A より A + B = 0 であり、A - B = 2A、AB = -A2 なので、
A2 + 2A = 0
より |A| = 0、a + d = -2 で、これらも (7)(8) を満たし、特別扱いする必要はなくなります。
最後に、p = 0 のときは B = qE より A - B = A - qE、AB = qA なので、
( 1 - q )A = qE
となり、これが成り立つのは A = [ q / ( 1 - q ) ]E ( q ≠ 1 ) のときに限ります。r = q / ( 1 - q ) とすれば q = r / ( 1 + r ) なので、
B = [ r / ( 1 + r ) ]E 但し A = rE
となります。
B の一次式を書くと、
B = pA + [ ( p + 1 )2 / p ]E
但し、|A| = [ ( p + 1 ) / p ]2 かつ a + d = -( 2p2 + p + 1 ) / p2
となります。例えば p = 1 のとき、B = A + 4E となります。また、|A| = 4、a + d = -4 です。これを満たす A として
があります。このとき、
となり、
より ( A + B )2 = 0 となります。
イエスが磔刑にされたのが云々というのはウソのようで、はっきりしたことはわかってないみたいですね。中世の頃から始まった迷信だそうですが、日本ではやはりあの映画から有名になったのではないでしょうか。一作目は面白かったと思います。二作目以降も見たような気もしますがほとんど覚えてません。ジェイソンが首吊り状態になっても自力でほどいてしまうシーンを覚えているんですけど、あれは何作目だったんでしょうかね。
今回は「マテマティカ 2」さんから拾った問題です。かなり苦戦した上に、合っているかどうか自信は全くありません。せっかく解いたので載せておきます。
-----
二次正方行列 A, B が次の二条件を満たしている。
(i) A - B = AB
(ii) ( A + B )n = 0 となる正の整数 n が存在する
このとき、B を A と E の一次式で表わせ。
まず、次の命題を証明します。
二次行列 A が逆行列を持たないとき、An = [ tr(A) ]n-1A
但し、tr(A) は A の対角成分の和とする。
| A = | | | a | c | | |
| | | b | d | | |
とします。このとき、
| A2 = | | | a | c | || | a | c | | | = | | | a2+bc | ac+cd | | |
| | | b | d | || | b | d | | | | | ab+bd | bc+d2 | | |
となりますが、A が逆行列を持たないとき ad - bc = 0 なので、ad = bc より
| A2 = | | | a2+ad | c(a+d) | | | = | | | a(a+d) | c(a+d) | | | =(a+d)A |
| | | b(a+d) | ad+d2 | | | | | c(a+d) | d(a+d) | | |
となります。
An = (a+d)n-1A が成り立つと仮定します。このとき
| An+1 | = | | | a(a+d)n-1 | c(a+d)n-1 | || | a | c | | |
| | | b(a+d)n-1 | d(a+d)n-1 | || | b | d | | | ||
| = | | | (a2+bc)(a+d)n-1 | (ac+cd)(a+d)n-1 | | |
| | | (ab+bd)(a+d)n-1 | (bc+d2)(a+d)n-1 | | |
| = | | | a(a+d)(a+d)n-1 | c(a+d)(a+d)n-1 | | |
| | | b(a+d)(a+d)n-1 | d(a+d)(a+d)n-1 | | |
= (a+d)nA
なので、帰納法により命題が証明されました。
An = 0 のとき、A が逆行列を持てばそれを n - 1 回掛けることで A = 0 となり、0 は逆行列を持たないので矛盾します。従って、A ≠ 0 のとき、An = 0 が成り立つならば、A は逆行列を持ちません。このとき、An = (a+d)n-1A = 0 が成り立つので、a + d = 0 かつ |A| = 0 であることになります。A2 = (a+d)A なので、An = 0 となる n が存在するならばその最小値は 1 か 2 のいずれかであることになります ( n = 1 ならば A = 0 です )。
( A + B )n = 0 が成り立つとき、
| B = | | | e | g | | |
| | | f | h | | |
とすれば
a + e + d + h = 0 --- (1)
| A + B | = ( a + e )( d + h ) - ( b + f )( c + g ) = 0 --- (2)
が成り立ちます。B = pA + qE ( 但し p ≠ 0 ) とすると、
| B = | | | pa+q | pc | | |
| | | pb | pd+q | | |
なので、(1) より
a + ( pa + q ) + d + ( pd + q ) = ( p + 1 )( a + d ) + 2q = 0 --- (1')
であり、(2) より
[ a + ( pa + q ) ][ d + ( pd + q ) ] - ( b + pb )( c + pc )
= [ ( p + 1 )a + q ][ ( p + 1 )d + q ] - ( p + 1 )2bc
= ( p + 1 )2( ad - bc ) + q( p + 1 )( a + d ) + q2 = 0 --- (2')
になります。
(1') を (2') に代入して整理すると、
( p + 1 )2|A| = q2 --- (3)
となります。次に、
A - B = ( 1 - p )A - qE
AB = pA2 + qA
なので、A - B = AB ならば
( 1 - p )A - qE = pA2 + qA
となります。これを整理すると
A2 - [ ( 1 - p - q ) / p ]A + ( q / p )E = 0
となりますが、ケーリー・ハミルトンの公式から
( 1 - p - q ) / p = a + d --- (4)
q / p = |A| --- (5)
が成り立つ必要があります。従って、(3),(5) から
q2 / ( p + 1 )2 = q / p ( 但し p ≠ -1 とする ) より
q = ( p + 1 )2 / p --- (6)
となり、(5) に代入して
|A| = [ ( p + 1 ) / p ]2 --- (7)
(4) に代入して
{ 1 - p - [ ( p + 1 )2 / p ] } / p
= [ p - p2 - ( p2 + 2p + 1 ) ] / p2
= -( 2p2 + p + 1 ) / p2 = a + d --- (8)
となります。(7)(8) を満たす p が存在するとき、(6) によって q が決定し、B の一次式も決まります。
p = -1 のとき、(3) より q = 0 なので (6) を満たします。B = -A より A + B = 0 であり、A - B = 2A、AB = -A2 なので、
A2 + 2A = 0
より |A| = 0、a + d = -2 で、これらも (7)(8) を満たし、特別扱いする必要はなくなります。
最後に、p = 0 のときは B = qE より A - B = A - qE、AB = qA なので、
( 1 - q )A = qE
となり、これが成り立つのは A = [ q / ( 1 - q ) ]E ( q ≠ 1 ) のときに限ります。r = q / ( 1 - q ) とすれば q = r / ( 1 + r ) なので、
B = [ r / ( 1 + r ) ]E 但し A = rE
となります。
B の一次式を書くと、
B = pA + [ ( p + 1 )2 / p ]E
但し、|A| = [ ( p + 1 ) / p ]2 かつ a + d = -( 2p2 + p + 1 ) / p2
となります。例えば p = 1 のとき、B = A + 4E となります。また、|A| = 4、a + d = -4 です。これを満たす A として
| A = | | | -1 | -1 | | |
| | | 1 | -3 | | |
があります。このとき、
| B = A + 4E = | | | 3 | -1 | | |
| | | 1 | 1 | | |
| A - B = | | | -4 | 0 | | |
| | | 0 | -4 | | |
| AB = | | | -4 | 0 | | |
| | | 0 | -4 | | |
となり、
| A + B = | | | 2 | -2 | | |
| | | 2 | -2 | | |
より ( A + B )2 = 0 となります。
2016年05月09日
いつの間にか夏
いつの間にか「立夏」を過ぎていたんですね。すでに蒸し暑い状態が続いているように思います。
「数学問題bot」から二年前に拾った問題です。合ってるかどうか、あまり自信はありません。
-----
n個の1の間すべてに四則演算のいずれかの記号を書いて式を作る(カッコは使用不可)とき、答えが1になるものは何通りあるか。例:n=2なら1×1と1÷1の2通り (DrGojiMoriCun様)。
×と÷は値を変化させないので、どのように並んでいても必ず 1 になります。よって、計算結果が 1 になるかどうかは + と - の数だけで決まり、その数がゼロも含めて等しい場合だけ 1 になります。
n 個の 1 の間には n - 1 個の演算子が入れられるので、その中に + と - を並べる場合の数を、全ての×と÷の並べ方に対して求めれば目的の数が得られます。
+ と - を等しい数だけ並べる場合、その数はゼロから ( n - 1 ) / 2 ( n が奇数のとき ) または ( n - 2 ) / 2 ( n が偶数のとき ) となります。ゼロ個の場合から順番に考えてみます。
+, - がゼロ個なら、×,÷は n - 1 箇所に任意に入れられるので、2n-1 通りの並べ方があります。
+, - が 1 個ずつなら、n - 1 箇所の中に + は n - 1 通りの入れ方があり、それぞれに対して - は n - 2 通りの入れ方があるので、( n - 1 )( n - 2 ) 通りの並べ方があります。残りの n - 3 箇所に×,÷は任意に入れられるので、それぞれに対しさらに 2n-3 通りの並べ方があります。よって、2n-3( n - 1 )( n - 2 ) 通りの入れ方があることになります。
一般化して +, - が k 個ずつなら、n - 1 箇所の中に + は n-1Ck 通りの入れ方があり、それぞれに対して - は残り n - k - 1 箇所に n-k-1Ck 通りの入れ方があるので、n-1Ck・n-k-1Ck 通りの並べ方があります。残りの n - 2k - 1 箇所に×,÷は任意に入れられるので、それぞれに対しさらに 2n-2k-1 通りの並べ方があり、2n-2k-1n-1Ck・n-k-1Ck 通りの入れ方があることになります。
これが 0 から ( n - 1 ) / 2 ( n が奇数のとき ) または ( n - 2 ) / 2 ( n が偶数のとき ) まであるので、
Σk{0→(n-1)/2}( 2n-2k-1n-1Ck・n-k-1Ck ) ( n が奇数のとき )
Σk{0→(n-2)/2}( 2n-2k-1n-1Ck・n-k-1Ck ) ( n が偶数のとき )
が求める解となります。n = 2 のときは、
Σk{0→0}( 22-2k-11Ck・1-kCk ) = 2
で、n = 3 のときは
Σk{0→1}( 22-2k2Ck・2-kCk )
= 222C0・2C0 + 202C1・1C1
= 4 + 2 = 6
で、1×1×1, 1×1÷1, 1÷1×1, 1÷1÷1, 1+1-1, 1-1+1 が該当します。さらに n = 4 なら
Σk{0→1}( 23-2k3Ck・3-kCk )
= 233C0・3C0 + 213C1・2C1
= 8 + 12 = 20
で、
1×1×1×1, 1×1×1÷1, 1×1÷1×1, 1÷1×1×1, 1×1÷1÷1, 1÷1×1÷1, 1÷1÷1×1, 1÷1÷1÷1,
1×1+1-1, 1×1-1+1, 1÷1+1-1, 1÷1-1+1, 1+1×1-1, 1-1×1+1, 1+1÷1-1, 1-1÷1+1,
1+1-1×1, 1-1+1×1, 1+1-1÷1, 1-1+1÷1
が該当します。
「数学問題bot」から二年前に拾った問題です。合ってるかどうか、あまり自信はありません。
-----
n個の1の間すべてに四則演算のいずれかの記号を書いて式を作る(カッコは使用不可)とき、答えが1になるものは何通りあるか。例:n=2なら1×1と1÷1の2通り (DrGojiMoriCun様)。
×と÷は値を変化させないので、どのように並んでいても必ず 1 になります。よって、計算結果が 1 になるかどうかは + と - の数だけで決まり、その数がゼロも含めて等しい場合だけ 1 になります。
n 個の 1 の間には n - 1 個の演算子が入れられるので、その中に + と - を並べる場合の数を、全ての×と÷の並べ方に対して求めれば目的の数が得られます。
+ と - を等しい数だけ並べる場合、その数はゼロから ( n - 1 ) / 2 ( n が奇数のとき ) または ( n - 2 ) / 2 ( n が偶数のとき ) となります。ゼロ個の場合から順番に考えてみます。
+, - がゼロ個なら、×,÷は n - 1 箇所に任意に入れられるので、2n-1 通りの並べ方があります。
+, - が 1 個ずつなら、n - 1 箇所の中に + は n - 1 通りの入れ方があり、それぞれに対して - は n - 2 通りの入れ方があるので、( n - 1 )( n - 2 ) 通りの並べ方があります。残りの n - 3 箇所に×,÷は任意に入れられるので、それぞれに対しさらに 2n-3 通りの並べ方があります。よって、2n-3( n - 1 )( n - 2 ) 通りの入れ方があることになります。
一般化して +, - が k 個ずつなら、n - 1 箇所の中に + は n-1Ck 通りの入れ方があり、それぞれに対して - は残り n - k - 1 箇所に n-k-1Ck 通りの入れ方があるので、n-1Ck・n-k-1Ck 通りの並べ方があります。残りの n - 2k - 1 箇所に×,÷は任意に入れられるので、それぞれに対しさらに 2n-2k-1 通りの並べ方があり、2n-2k-1n-1Ck・n-k-1Ck 通りの入れ方があることになります。
これが 0 から ( n - 1 ) / 2 ( n が奇数のとき ) または ( n - 2 ) / 2 ( n が偶数のとき ) まであるので、
Σk{0→(n-1)/2}( 2n-2k-1n-1Ck・n-k-1Ck ) ( n が奇数のとき )
Σk{0→(n-2)/2}( 2n-2k-1n-1Ck・n-k-1Ck ) ( n が偶数のとき )
が求める解となります。n = 2 のときは、
Σk{0→0}( 22-2k-11Ck・1-kCk ) = 2
で、n = 3 のときは
Σk{0→1}( 22-2k2Ck・2-kCk )
= 222C0・2C0 + 202C1・1C1
= 4 + 2 = 6
で、1×1×1, 1×1÷1, 1÷1×1, 1÷1÷1, 1+1-1, 1-1+1 が該当します。さらに n = 4 なら
Σk{0→1}( 23-2k3Ck・3-kCk )
= 233C0・3C0 + 213C1・2C1
= 8 + 12 = 20
で、
1×1×1×1, 1×1×1÷1, 1×1÷1×1, 1÷1×1×1, 1×1÷1÷1, 1÷1×1÷1, 1÷1÷1×1, 1÷1÷1÷1,
1×1+1-1, 1×1-1+1, 1÷1+1-1, 1÷1-1+1, 1+1×1-1, 1-1×1+1, 1+1÷1-1, 1-1÷1+1,
1+1-1×1, 1-1+1×1, 1+1-1÷1, 1-1+1÷1
が該当します。
2016年05月02日
頭の体操
連休に入り、急激に暑くなってきました。明日は少し気温が下がるようですが、今度は雨になるみたいですね。
午後の空いた時間で頭の体操。「数学問題bot」さんから拾った問題です。合っている保証はありません。
-----
空間内に四面体 ABCD を考える。このとき、4 つの頂点 A, B, C, D を同時に通る球面が存在することを示せ ( 11 京大・理 )
四面体 ABCD に対して座標軸は任意に決められるので、頂点 A を原点とし、B( 2a, 0, 0 )、C( 2b, 2c, 0 )、D( 2d, 2e, 2f ) とします。
この時、辺 AB は x 軸上に、三角形 ABC は xy 平面上にあります。また、明らかに c ≠ 0、f ≠ 0 になります。
四面体の内点 P( xc, yc, zc ) に対し、|AP| = |BP| = |CP| = |DP| = ( xc2 + yc2 + zc2 )1/2 が成り立てば、P は求める球面の中心ということになるので、P が存在することを示せば十分です。三角形 PAB, PAC, PAD はそれぞれ二等辺三角形となるので、P は辺 AB, AC, AD の中点を通り各辺に垂直な平面の交点となります。平面の方程式は、
a( x - a ) = 0
b( x - b ) + c( y - c ) = 0
d( x - d ) + e( y - e ) + f( z - f ) = 0
となるので、
xc = a
yc = c - b( a - b ) / c
zc = f - d( a - d ) / f - e( yc - e ) / f
となります。この式を元に、|BP|2, |CP|2, |DP|2 を求めると、
|BP|2
= ( 2a - a )2 + ( 0 - yc )2 + ( 0 - zc )2
= a2 + yc2 + zc2
= xc2 + yc2 + zc2
|CP|2
= ( 2b - a )2 + { 2c - [ c - b( a - b ) / c ] }2 + ( 0 - zc )2
= a2 - 4ab + 4b2 + [ c - b( a - b ) / c ]2 - 4c[ c - b( a - b ) / c ] +4c2 + zc2
= xc2 + yc2 + zc2 - 4ab + 4b2 - 4c2 + 4ab - 4b2 +4c2
= xc2 + yc2 + zc2
|DP|2
= ( 2d - a )2 + ( 2e - yc )2 + { 2f - [ f - d( a - d ) / f - e( yc - e ) / f ] }2
= ( 2d - a )2 + ( 2e - yc )2 + { f + d( a - d ) / f + e( yc - e ) / f ] }2
= a2 - 4ad + 4d2 + yc2 - 4e・yc + 4e2 + [ f - d( a - d ) / f - e( yc - e ) / f ]2 +4[ d( a - d ) + e( yc - e ) ]
= xc2 + yc2 + zc2 - 4ad + 4d2 - 4e・yc + 4e2 +4ad - 4d2 + 4e・yc - 4e2
= xc2 + yc2 + zc2
となるので、|AP| = |BP| = |CP| = |DP| が成り立ち、命題が証明されました。
午後の空いた時間で頭の体操。「数学問題bot」さんから拾った問題です。合っている保証はありません。
-----
空間内に四面体 ABCD を考える。このとき、4 つの頂点 A, B, C, D を同時に通る球面が存在することを示せ ( 11 京大・理 )
四面体 ABCD に対して座標軸は任意に決められるので、頂点 A を原点とし、B( 2a, 0, 0 )、C( 2b, 2c, 0 )、D( 2d, 2e, 2f ) とします。
この時、辺 AB は x 軸上に、三角形 ABC は xy 平面上にあります。また、明らかに c ≠ 0、f ≠ 0 になります。
四面体の内点 P( xc, yc, zc ) に対し、|AP| = |BP| = |CP| = |DP| = ( xc2 + yc2 + zc2 )1/2 が成り立てば、P は求める球面の中心ということになるので、P が存在することを示せば十分です。三角形 PAB, PAC, PAD はそれぞれ二等辺三角形となるので、P は辺 AB, AC, AD の中点を通り各辺に垂直な平面の交点となります。平面の方程式は、
a( x - a ) = 0
b( x - b ) + c( y - c ) = 0
d( x - d ) + e( y - e ) + f( z - f ) = 0
となるので、
xc = a
yc = c - b( a - b ) / c
zc = f - d( a - d ) / f - e( yc - e ) / f
となります。この式を元に、|BP|2, |CP|2, |DP|2 を求めると、
|BP|2
= ( 2a - a )2 + ( 0 - yc )2 + ( 0 - zc )2
= a2 + yc2 + zc2
= xc2 + yc2 + zc2
|CP|2
= ( 2b - a )2 + { 2c - [ c - b( a - b ) / c ] }2 + ( 0 - zc )2
= a2 - 4ab + 4b2 + [ c - b( a - b ) / c ]2 - 4c[ c - b( a - b ) / c ] +4c2 + zc2
= xc2 + yc2 + zc2 - 4ab + 4b2 - 4c2 + 4ab - 4b2 +4c2
= xc2 + yc2 + zc2
|DP|2
= ( 2d - a )2 + ( 2e - yc )2 + { 2f - [ f - d( a - d ) / f - e( yc - e ) / f ] }2
= ( 2d - a )2 + ( 2e - yc )2 + { f + d( a - d ) / f + e( yc - e ) / f ] }2
= a2 - 4ad + 4d2 + yc2 - 4e・yc + 4e2 + [ f - d( a - d ) / f - e( yc - e ) / f ]2 +4[ d( a - d ) + e( yc - e ) ]
= xc2 + yc2 + zc2 - 4ad + 4d2 - 4e・yc + 4e2 +4ad - 4d2 + 4e・yc - 4e2
= xc2 + yc2 + zc2
となるので、|AP| = |BP| = |CP| = |DP| が成り立ち、命題が証明されました。
2016年04月30日
若鯱家
少し前に初めて若鯱家に入りました。
名古屋ではカレーうどん専門店として有名ですが、今まで入ったことがなかったんですよね。で、外出時に一度食べてみようと思い立ったわけですが、予想以上に熱くて食べるのに苦労しました。しかし、辛さはそうでもなく、辛いもの好きには物足りないかもしれません。自分にとってはちょうどよかったですが。
昔、拾った大学入試問題です。例によって合っている保証はありません。
-----
n を自然数とし In = ∫{0→1} xnex dx とおく。 (中略) 3) lim{n→∞} n( n * In - e ) を求めよ ( 01 大分医科大 )
部分積分法を使って
In
= ∫{0→1} xnex dx
= [ ( 1 / n )xn+1ex ]{0→1} - ∫{0→1} ( 1 / n )xn+1ex dx
= e / n - [ [ 1 / n( n + 1 ) ]xn+2ex ]{0→1} + ∫{0→1} [ 1 / n( n + 1 ) ]xn+2ex dx
= e / n - e / n( n + 1 ) + e / n( n + 1 )( n + 2 ) - ... + ( -1 )k+1∫{0→1} [ ( n - 1 )! / ( n + k )! ]xn+kex dx
= e / n + eΣk{1→∞}( ( -1 )k( n - 1 )! / ( n + k )! )
となるので、
nIn - e
= n[ e / n + eΣk{1→∞}( ( -1 )k( n - 1 )! / ( n + k )! ) ] - e
= eΣk{1→∞}( ( -1 )kn( n - 1 )! / ( n + k )! )
= eΣk{1→∞}( ( -1 )kn! / ( n + k )! )
であり、
n( nIn - e )
= eΣk{1→∞}( ( -1 )knn! / ( n + k )! )
= e{ -1 / ( 1 + 1 / n ) + 1 / [ ( n + 1 )( n + 2 ) / n ] - ... } → -e (n→∞)
となります。
名古屋ではカレーうどん専門店として有名ですが、今まで入ったことがなかったんですよね。で、外出時に一度食べてみようと思い立ったわけですが、予想以上に熱くて食べるのに苦労しました。しかし、辛さはそうでもなく、辛いもの好きには物足りないかもしれません。自分にとってはちょうどよかったですが。
昔、拾った大学入試問題です。例によって合っている保証はありません。
-----
n を自然数とし In = ∫{0→1} xnex dx とおく。 (中略) 3) lim{n→∞} n( n * In - e ) を求めよ ( 01 大分医科大 )
部分積分法を使って
In
= ∫{0→1} xnex dx
= [ ( 1 / n )xn+1ex ]{0→1} - ∫{0→1} ( 1 / n )xn+1ex dx
= e / n - [ [ 1 / n( n + 1 ) ]xn+2ex ]{0→1} + ∫{0→1} [ 1 / n( n + 1 ) ]xn+2ex dx
= e / n - e / n( n + 1 ) + e / n( n + 1 )( n + 2 ) - ... + ( -1 )k+1∫{0→1} [ ( n - 1 )! / ( n + k )! ]xn+kex dx
= e / n + eΣk{1→∞}( ( -1 )k( n - 1 )! / ( n + k )! )
となるので、
nIn - e
= n[ e / n + eΣk{1→∞}( ( -1 )k( n - 1 )! / ( n + k )! ) ] - e
= eΣk{1→∞}( ( -1 )kn( n - 1 )! / ( n + k )! )
= eΣk{1→∞}( ( -1 )kn! / ( n + k )! )
であり、
n( nIn - e )
= eΣk{1→∞}( ( -1 )knn! / ( n + k )! )
= e{ -1 / ( 1 + 1 / n ) + 1 / [ ( n + 1 )( n + 2 ) / n ] - ... } → -e (n→∞)
となります。
2016年04月25日
囲碁で七冠達成
囲碁棋士の井山裕太さんが七冠達成するかというニュースを見たのが少し前。そして最近、ついに達成したとのニュースが流れ、新聞でも大きく報じられていました。師匠からは「自由に打て」と指導されていたというので、おそらくその天賦の才能を見抜いていたんじゃないでしょうか。その代わり礼儀にはかなり厳しかったそうです。グーグルの AlphaGo との対戦を見てみたいものです。
囲碁のルール、実は全く知りません。NHK で囲碁の対局をやっていて、たまに見ることがあるんですけどやっぱり何をやっているのか全く把握できません。いや、見ているうちに何となくわかるんじゃないかと期待したのですが無理でした。それならルールを覚えればいいじゃないかと言われそうですが、そこまで興味もなく。
話は変わって、アルゴリズムのコーナーを更新しました。ウェーブレット変換の後半部になりますが、今回は JPEG2000 で使われている変換方法についても新たに追加しています。かなり見直しをしていますので、興味のある方はぜひご覧ください。
リンク先 ... 圧縮アルゴリズム (9) ウェーブレット変換 -2-
囲碁にちなんでこんな問題を選んでみました。
-----
白石 180 個と黒石 181 個、計 361 個の石が横に一列に並んでいる。石がどう並んでいても、以下の条件を満たす黒の石が少なくとも一つあることを示せ。「その黒の石とそれより右にある石をすべて除くと、残りは白黒同数となる。ただし、石が一つも残らない場合も同数とみなす。」 ( 01 東大文系 )
黒石が先頭にあるとその石以降を取り除けば同数となるので、先頭は必ず白石であると仮定できます。また、黒石が末尾にあると、それを取り除けばどちらも同数の 180 個になるので、末尾もやはり白石と仮定できます。
白・黒の石の並び方に関係なく、黒石のある箇所で白石の数を黒石が超えれば条件を満たすことになるので、条件を満たさずに並べるためには黒石の数が白石の数を超えないように並べなければなりません。白石の数は 180 個なので、黒石も 180 個までは条件を満たさないように並べることができます(簡単な例としては、最初に白石を 180 個、その後に黒石を 180 個並べた場合です)。しかし、最後に黒石が一つ余ってしまうため、それを並べてしまえば条件を満たしてしまいます。なお、白石が末尾になるように白・黒同数の 180 個を条件を満たさずに並べることはできません。なぜなら、白石が末尾にあるときはその前にある黒石の数が白石の数を超えてしまい、条件を満たしてしまうからです。よって、命題が証明されました。
この問題は、白石の数を任意の N 個とし、黒石の数を N + 1 個とした場合でも成り立ちます。これは帰納法で証明できます。
N = 1 のときは、黒石がどちらかの端にならないように並べることが不可能なので、命題が成り立ちます。N 個の場合に命題が成り立つと仮定した時、これに白・黒ひとつずつの石を加える事を考えます。条件を満たす黒石の位置(これを P と名付けます)に対し、加える石を両方とも P より先頭側か末尾側のどちらか一方に任意に入れた場合は P の位置で条件が成り立ってしまうため、条件を満たさないようにしたければ、それぞれの石は異なる側に置く必要があります。白を P より先頭側においた場合、P の位置で白・黒同数となり、それ以降は黒石が一つだけ多い状態になります。その部分は白石の数が N 以下なので、条件を満たす位置が新たに見つかることになります。逆に黒石を P より先頭側においた場合、P を含めた末尾側が白・黒同数となり、P を除いた先頭側が黒の一個多い状態となります。これも白石の数は N 個以下なので条件を満たす黒石が見つかり条件を満たすことになります。
よって、命題が証明されました。
囲碁のルール、実は全く知りません。NHK で囲碁の対局をやっていて、たまに見ることがあるんですけどやっぱり何をやっているのか全く把握できません。いや、見ているうちに何となくわかるんじゃないかと期待したのですが無理でした。それならルールを覚えればいいじゃないかと言われそうですが、そこまで興味もなく。
話は変わって、アルゴリズムのコーナーを更新しました。ウェーブレット変換の後半部になりますが、今回は JPEG2000 で使われている変換方法についても新たに追加しています。かなり見直しをしていますので、興味のある方はぜひご覧ください。
リンク先 ... 圧縮アルゴリズム (9) ウェーブレット変換 -2-
囲碁にちなんでこんな問題を選んでみました。
-----
白石 180 個と黒石 181 個、計 361 個の石が横に一列に並んでいる。石がどう並んでいても、以下の条件を満たす黒の石が少なくとも一つあることを示せ。「その黒の石とそれより右にある石をすべて除くと、残りは白黒同数となる。ただし、石が一つも残らない場合も同数とみなす。」 ( 01 東大文系 )
黒石が先頭にあるとその石以降を取り除けば同数となるので、先頭は必ず白石であると仮定できます。また、黒石が末尾にあると、それを取り除けばどちらも同数の 180 個になるので、末尾もやはり白石と仮定できます。
白・黒の石の並び方に関係なく、黒石のある箇所で白石の数を黒石が超えれば条件を満たすことになるので、条件を満たさずに並べるためには黒石の数が白石の数を超えないように並べなければなりません。白石の数は 180 個なので、黒石も 180 個までは条件を満たさないように並べることができます(簡単な例としては、最初に白石を 180 個、その後に黒石を 180 個並べた場合です)。しかし、最後に黒石が一つ余ってしまうため、それを並べてしまえば条件を満たしてしまいます。なお、白石が末尾になるように白・黒同数の 180 個を条件を満たさずに並べることはできません。なぜなら、白石が末尾にあるときはその前にある黒石の数が白石の数を超えてしまい、条件を満たしてしまうからです。よって、命題が証明されました。
この問題は、白石の数を任意の N 個とし、黒石の数を N + 1 個とした場合でも成り立ちます。これは帰納法で証明できます。
N = 1 のときは、黒石がどちらかの端にならないように並べることが不可能なので、命題が成り立ちます。N 個の場合に命題が成り立つと仮定した時、これに白・黒ひとつずつの石を加える事を考えます。条件を満たす黒石の位置(これを P と名付けます)に対し、加える石を両方とも P より先頭側か末尾側のどちらか一方に任意に入れた場合は P の位置で条件が成り立ってしまうため、条件を満たさないようにしたければ、それぞれの石は異なる側に置く必要があります。白を P より先頭側においた場合、P の位置で白・黒同数となり、それ以降は黒石が一つだけ多い状態になります。その部分は白石の数が N 以下なので、条件を満たす位置が新たに見つかることになります。逆に黒石を P より先頭側においた場合、P を含めた末尾側が白・黒同数となり、P を除いた先頭側が黒の一個多い状態となります。これも白石の数は N 個以下なので条件を満たす黒石が見つかり条件を満たすことになります。
よって、命題が証明されました。
2016年04月23日
ウェーブレット変換
現在、ウェーブレット変換・多重解像度解析あたりを再度勉強中です。非常に奥が深い、というか難しいです。
ようやく JPEG2000 で使われているフィルタの内容を理解することができました。でも、他の変換法に比べてどう違うのか、評価する方法がわからず現在調査中です。まだ道程は長そうです。
息抜きに、昔拾った問題を解いてみました。合っている保証はありません。
-----
a は定数。x151 を x5 - a で割った余りを求めよ。 ( 09 慶應 )
x151 = ( x5 - a )( x146 + ax141 + a2x136 + ... + a28x6 + a29x ) + a30x より a30x
ようやく JPEG2000 で使われているフィルタの内容を理解することができました。でも、他の変換法に比べてどう違うのか、評価する方法がわからず現在調査中です。まだ道程は長そうです。
息抜きに、昔拾った問題を解いてみました。合っている保証はありません。
-----
a は定数。x151 を x5 - a で割った余りを求めよ。 ( 09 慶應 )
x151 = ( x5 - a )( x146 + ax141 + a2x136 + ... + a28x6 + a29x ) + a30x より a30x
2016年04月13日
テイラー展開
さっきから大雨降ってます。明日も雨の予報でしたっけ?
ウェーブレット変換はかなり奥が深く、本格的に勉強しようとすると大変です。以前まとめたドキュメントはいろいろと変な箇所があって、まずはそれだけでも修正しようと思っていますが、さらに新しい内容を追加しようとするとまだ理解度が不足しているのでかなり時間が掛かりそうです。実はもう一つ、統計の分野の PLS をまとめてみようとも思っていて、どちらを優先するか悩んでます。まず、いまのところはウェーブレット変換の方を優先しています。
昔拾った問題をまた解いてみましたが、今回はテーラー展開を使っています。高校の時は確か習わないのでこれはアウトかな?
例によって合っている保証なしです。
-----
1) 実数 x が -1 < x < 1, x ≠ 0 を満たすとき、( 1 - x )1-1/x < ( 1 + x )1/x を示せ。
2) 次の不等式 0.9999101 < 0.99 < 0.9999100 を示せ ( 09 東大理系 5 )
1)
log( 1 + x )1/x = ( 1 / x )log( 1 + x ) より、f(x) = log( 1 + x ) をテーラー展開すると、
f(1)(x) = ( 1 + x )-1
f(2)(x) = -( 1 + x )-2
f(3)(x) = 2( 1 + x )-3
:
f(k)(x) = ( -1 )k-1( k - 1 )!( 1 + x )-k
より、
f(x)
= f(0) + Σk{1→∞}( ( 1 / k! )f(k)(0)xk )
= Σk{1→∞}( ( 1 / k! )( -1 )k-1( k - 1 )!xk )
= Σk{1→∞}( ( -1 )k-1xk / k )
なので
log( 1 + x )1/x = Σk{1→∞}( ( -1 )k-1xk-1 / k )
となります。また、log( 1 - x )1-1/x = ( 1 - 1 / x )log( 1 - x ) も、g(x) = log( 1 - x ) をテーラー展開すれば ( 先の式に対して x を -x に代えるだけなので )
g(x) = Σk{1→∞}( -xk / k )
より
( 1 - 1 / x )log( 1 - x )
= [ ( x - 1 ) / x ]Σk{1→∞}( -xk / k )
= ( 1 - x )Σk{1→∞}( xk-1 / k )
となります。両者を引き算すると
log( 1 + x )1/x - log( 1 - x )1-1/x
= Σk{1→∞}( ( -1 )k-1xk-1 / k ) - ( 1 - x )Σk{1→∞}( xk-1 / k )
= Σk{1→∞}( [ ( -1 )k-1xk-1 / k - xk-1 / k ] + xk / k )
= Σk{1→∞}( [ ( -1 )k-1 - 1 ]xk-1 / k + xk / k )
= Σk{1→∞}( -2x2k-1 / 2k + x2k-1 / ( 2k - 1 ) + x2k / 2k )
= Σk{1→∞}( x2k / 2k - [ ( k - 1 ) / k( 2k - 1 ) ] }x2k-1 )
= Σk{1→∞}( x2k / 2k - [ k / ( k + 1 )( 2k + 1 ) ] }x2k+1 )
= Σk{1→∞}( { 1 / 2k - [ kx / ( k + 1 )( 2k + 1 ) ] }x2k )
-1 < x < 0 のとき、kx / ( k + 1 )( 2k + 1 ) < 0 かつ x2k > 0 なので (右辺) > 0 になります。
0 < x < 1 のとき、(右辺) > Σk{1→∞}( 1 / 2k - [ k / ( k + 1 )( 2k + 1 ) ] ) で、
1 / 2k - [ k / ( k + 1 )( 2k + 1 ) ]
= [ ( k + 1 )( 2k + 1 ) - 2k2 ] / 2k( k + 1 )( 2k + 1 )
= ( 3k + 1 ) / 2k( k + 1 )( 2k + 1 ) > 0 なので、
0 < x < 1 かつ x ≠ 0 ならば命題が成り立つことが証明されました。
2)
0.9999101 = ( 0.99・1.01 )101 = 0.99101・1.01101 より
1.01101
= [ 1 - ( -0.01 ) ]1-1/(-0.01)
< [ 1 + ( -0.01 ) ]-1/0.01
= 0.99-100
よって 0.9999101 < 0.99101・0.99-100 = 0.99 となります。
また、0.9999100 = ( 0.99・1.01 )100 = 0.99100・1.01100 より
1.01100
= ( 1 + 0.01 )1/0.01
> ( 1 - 0.01 )1-1/0.01
= 0.99-99
よって 0.9999100 > 0.99100・0.99-99 = 0.99 となります。
以上から、命題が成り立つことが証明されました。
ウェーブレット変換はかなり奥が深く、本格的に勉強しようとすると大変です。以前まとめたドキュメントはいろいろと変な箇所があって、まずはそれだけでも修正しようと思っていますが、さらに新しい内容を追加しようとするとまだ理解度が不足しているのでかなり時間が掛かりそうです。実はもう一つ、統計の分野の PLS をまとめてみようとも思っていて、どちらを優先するか悩んでます。まず、いまのところはウェーブレット変換の方を優先しています。
昔拾った問題をまた解いてみましたが、今回はテーラー展開を使っています。高校の時は確か習わないのでこれはアウトかな?
例によって合っている保証なしです。
-----
1) 実数 x が -1 < x < 1, x ≠ 0 を満たすとき、( 1 - x )1-1/x < ( 1 + x )1/x を示せ。
2) 次の不等式 0.9999101 < 0.99 < 0.9999100 を示せ ( 09 東大理系 5 )
1)
log( 1 + x )1/x = ( 1 / x )log( 1 + x ) より、f(x) = log( 1 + x ) をテーラー展開すると、
f(1)(x) = ( 1 + x )-1
f(2)(x) = -( 1 + x )-2
f(3)(x) = 2( 1 + x )-3
:
f(k)(x) = ( -1 )k-1( k - 1 )!( 1 + x )-k
より、
f(x)
= f(0) + Σk{1→∞}( ( 1 / k! )f(k)(0)xk )
= Σk{1→∞}( ( 1 / k! )( -1 )k-1( k - 1 )!xk )
= Σk{1→∞}( ( -1 )k-1xk / k )
なので
log( 1 + x )1/x = Σk{1→∞}( ( -1 )k-1xk-1 / k )
となります。また、log( 1 - x )1-1/x = ( 1 - 1 / x )log( 1 - x ) も、g(x) = log( 1 - x ) をテーラー展開すれば ( 先の式に対して x を -x に代えるだけなので )
g(x) = Σk{1→∞}( -xk / k )
より
( 1 - 1 / x )log( 1 - x )
= [ ( x - 1 ) / x ]Σk{1→∞}( -xk / k )
= ( 1 - x )Σk{1→∞}( xk-1 / k )
となります。両者を引き算すると
log( 1 + x )1/x - log( 1 - x )1-1/x
= Σk{1→∞}( ( -1 )k-1xk-1 / k ) - ( 1 - x )Σk{1→∞}( xk-1 / k )
= Σk{1→∞}( [ ( -1 )k-1xk-1 / k - xk-1 / k ] + xk / k )
= Σk{1→∞}( [ ( -1 )k-1 - 1 ]xk-1 / k + xk / k )
= Σk{1→∞}( -2x2k-1 / 2k + x2k-1 / ( 2k - 1 ) + x2k / 2k )
= Σk{1→∞}( x2k / 2k - [ ( k - 1 ) / k( 2k - 1 ) ] }x2k-1 )
= Σk{1→∞}( x2k / 2k - [ k / ( k + 1 )( 2k + 1 ) ] }x2k+1 )
= Σk{1→∞}( { 1 / 2k - [ kx / ( k + 1 )( 2k + 1 ) ] }x2k )
-1 < x < 0 のとき、kx / ( k + 1 )( 2k + 1 ) < 0 かつ x2k > 0 なので (右辺) > 0 になります。
0 < x < 1 のとき、(右辺) > Σk{1→∞}( 1 / 2k - [ k / ( k + 1 )( 2k + 1 ) ] ) で、
1 / 2k - [ k / ( k + 1 )( 2k + 1 ) ]
= [ ( k + 1 )( 2k + 1 ) - 2k2 ] / 2k( k + 1 )( 2k + 1 )
= ( 3k + 1 ) / 2k( k + 1 )( 2k + 1 ) > 0 なので、
0 < x < 1 かつ x ≠ 0 ならば命題が成り立つことが証明されました。
2)
0.9999101 = ( 0.99・1.01 )101 = 0.99101・1.01101 より
1.01101
= [ 1 - ( -0.01 ) ]1-1/(-0.01)
< [ 1 + ( -0.01 ) ]-1/0.01
= 0.99-100
よって 0.9999101 < 0.99101・0.99-100 = 0.99 となります。
また、0.9999100 = ( 0.99・1.01 )100 = 0.99100・1.01100 より
1.01100
= ( 1 + 0.01 )1/0.01
> ( 1 - 0.01 )1-1/0.01
= 0.99-99
よって 0.9999100 > 0.99100・0.99-99 = 0.99 となります。
以上から、命題が成り立つことが証明されました。
2016年04月10日
桜もそろそろ終わりかな
この間の雨で桜もだいぶ散ってしまいました。先週に散歩がてら満開の桜の木が撮影できたので載せておきます。

数学問題botから昔拾った問題です。うまい解き方が見つかったので公開。しかし、合っている保証なしです。
-----
正十角形の各頂点に 1 ~ 3 のいずれかの数を割り当て、それらの総和を S とする。1 が付けられた頂点が 5 個以上あり、かつ S ≤ 19 のとき、1 から S のどの自然数 n も連続する何頂点か ( 1 頂点でもよい ) に付けられた数の和として表せることを示せ ( 第 29 回シュプリンガー数学コンテスト )
1 が 5 つ以上あるので、残りの頂点は S ≤ 14 の範囲で割り当てる必要があります。従って、残りの頂点が全て 3 になる場合は除外できます。
まず、1 だけで構成された場合を考えると明らかに成り立ちます。次に、1 と 2 だけで構成されている場合を考えます。但し、1 は少なくとも 1 つは存在するとします。全体での和は S になるので、この中からどれか一つだけ 1 の頂点を除外すると、和が S - 1 になる連続した部分が得られます。その部分の両端には 1 か 2 が存在するので、
1) 1 があればその頂点を外し、
2) 2 しかかなければいずれかを外して前に除外した 1 を復活する
ことを繰り返します。このとき、最初に除外した頂点が 1 で、手順から少なくとも片側には前に 1 を除外したか、1 が復活して残っているので、前者なら 2) の手順が可能であり、後者なら 1) の手順が可能です。従って、1), 2) の手順は必ずできることが保証され、この場合は少なくとも一つの 1 があれば成り立ちます。
次に、3 を含めた場合を考えます。3 は最大でも 4 つしか含められないので、S が最大となる場合は 2 が一つ、3 が 4 つ含まれる場合です。そのため、必ずどこかに 1 が連続して二つ並んだ部分 { 1 1 } か 2 が 1 に挟まれた部分 { 1 2 1 } が存在します。なぜなら、1 以外の数を x としたとき、1 が連続しない並べ方は { 1 x 1 x 1 x 1 x 1 x } しかなく、x の少なくとも一つは 2 だからです。
まず、{ 1 1 } の場合を考えると、最初にこの部分を除外すれば残り 8 つの頂点が残ります。両端のうち片側のみに着目し、1 ならそれを除外すると和が一つ少ない部分が得られます。また、2 の場合はそれを除外して { 1 1 } を復活させると和が同数の部分になります。この後、1 を一つずつ除外すれば、和が 2 つ少ない部分まで得られることになります。3 だった場合はそれを除外して { 1 1 } を復活させると和が一つ少ない部分が得られ、2 の場合と同様の手順で和が 3 つ少ない部分まで得られます。端に除外された { 1 1 } があることが保証されているので、これは最後まで進めることができ、成り立つことが確認できます。
最後に { 1 2 1 } を持つ場合、除外する代わりに、この部分から片方向に順番に生成する方向で考えます。このとき、最初は 1 以外の数で、その後 1 とそれ以外の数が交互に得られることを考慮すると、次の数が 2 だったときは { 1 2 1 } の端の 1 を除外してからもう片側の 2 をつなぎ、次に先ほど除外した 1 をつなげば順番に 2 だけ大きな和まで生成することができます。また、3 の場合は端の { 1 2 } を除外して 3 をつなぎ、3 の次にある 1 をさらにつなぎます。今度は今つないだ 1 を除外して { 1 2 } の中の 2 だけをつなぎ、次は両端に残った 1 を順番につないでいきます。この操作によって、全ての和について連続した部分を生成することが可能となります。
以上から、命題が成り立つことが示されました。

数学問題botから昔拾った問題です。うまい解き方が見つかったので公開。しかし、合っている保証なしです。
-----
正十角形の各頂点に 1 ~ 3 のいずれかの数を割り当て、それらの総和を S とする。1 が付けられた頂点が 5 個以上あり、かつ S ≤ 19 のとき、1 から S のどの自然数 n も連続する何頂点か ( 1 頂点でもよい ) に付けられた数の和として表せることを示せ ( 第 29 回シュプリンガー数学コンテスト )
1 が 5 つ以上あるので、残りの頂点は S ≤ 14 の範囲で割り当てる必要があります。従って、残りの頂点が全て 3 になる場合は除外できます。
まず、1 だけで構成された場合を考えると明らかに成り立ちます。次に、1 と 2 だけで構成されている場合を考えます。但し、1 は少なくとも 1 つは存在するとします。全体での和は S になるので、この中からどれか一つだけ 1 の頂点を除外すると、和が S - 1 になる連続した部分が得られます。その部分の両端には 1 か 2 が存在するので、
1) 1 があればその頂点を外し、
2) 2 しかかなければいずれかを外して前に除外した 1 を復活する
ことを繰り返します。このとき、最初に除外した頂点が 1 で、手順から少なくとも片側には前に 1 を除外したか、1 が復活して残っているので、前者なら 2) の手順が可能であり、後者なら 1) の手順が可能です。従って、1), 2) の手順は必ずできることが保証され、この場合は少なくとも一つの 1 があれば成り立ちます。
次に、3 を含めた場合を考えます。3 は最大でも 4 つしか含められないので、S が最大となる場合は 2 が一つ、3 が 4 つ含まれる場合です。そのため、必ずどこかに 1 が連続して二つ並んだ部分 { 1 1 } か 2 が 1 に挟まれた部分 { 1 2 1 } が存在します。なぜなら、1 以外の数を x としたとき、1 が連続しない並べ方は { 1 x 1 x 1 x 1 x 1 x } しかなく、x の少なくとも一つは 2 だからです。
まず、{ 1 1 } の場合を考えると、最初にこの部分を除外すれば残り 8 つの頂点が残ります。両端のうち片側のみに着目し、1 ならそれを除外すると和が一つ少ない部分が得られます。また、2 の場合はそれを除外して { 1 1 } を復活させると和が同数の部分になります。この後、1 を一つずつ除外すれば、和が 2 つ少ない部分まで得られることになります。3 だった場合はそれを除外して { 1 1 } を復活させると和が一つ少ない部分が得られ、2 の場合と同様の手順で和が 3 つ少ない部分まで得られます。端に除外された { 1 1 } があることが保証されているので、これは最後まで進めることができ、成り立つことが確認できます。
最後に { 1 2 1 } を持つ場合、除外する代わりに、この部分から片方向に順番に生成する方向で考えます。このとき、最初は 1 以外の数で、その後 1 とそれ以外の数が交互に得られることを考慮すると、次の数が 2 だったときは { 1 2 1 } の端の 1 を除外してからもう片側の 2 をつなぎ、次に先ほど除外した 1 をつなげば順番に 2 だけ大きな和まで生成することができます。また、3 の場合は端の { 1 2 } を除外して 3 をつなぎ、3 の次にある 1 をさらにつなぎます。今度は今つないだ 1 を除外して { 1 2 } の中の 2 だけをつなぎ、次は両端に残った 1 を順番につないでいきます。この操作によって、全ての和について連続した部分を生成することが可能となります。
以上から、命題が成り立つことが示されました。
2016年03月31日
巨大な数によるべき乗計算
3 月も今日で終わりです。桜は明日あたりが満開になるかな。しかし、雨の予報が。。。
3 月に間に合わせる形で「アルゴリズムのコーナー」を更新しました。過去に公開した「ウェーブレット変換」の内容を見直しています。過去に作ったドキュメントをみると変な箇所や説明不足の部分もいろいろとあったのでかなり手直ししています。メインは多重解像度解析なのに、連続ウェーブレット変換の方が見直しに時間がかかりました。
そして、過去に拾ったまま放置していた問題を気合入れて解きました。ようやく暗算で計算できる方法を思いついたので紹介しておきます。
-----
1) 201123 の下 4 桁を求めよ。
2) 201123! の下 4 桁を求めよ ( cruz__F 様 )
以下、合同式を多用するので、先に定義といくつかの定理だけ示しておきます。
整数 m, k, q, r に対して m = qk + r となるとき、「m は k を法として r と合同である」といい、m ≡ r ( mod k ) と表します。これを「合同式」または「モジュラー演算」といいます。「時計算」と呼ばれることもあります。合同式では、m ≡ r ( mod k ) かつ n ≡ s ( mod k ) であるとき、
m ± n ≡ r ± s ( mod k )
m・n ≡ r・s ( mod k )
mn ≡ rn ( mod k )
が成り立ちます。
1) 二項定理より
201123
= ( 2000 + 11 )23
= 200023 + 23C1・200022・11 + ... + 23C22・2000・1122 + 1123
≡ 23・2000・1122 + 1123 ( mod 10000 )
となります。なぜなら、任意のゼロでない自然数 N と 1 より大きい自然数 a に対し、2000a・N ≡ 0 ( mod 10000 ) となるため、そのような項は無視できるからです。
23・2000・1122 + 1123 = 1122( 23・2000 + 11 )
より、1122 と 23・2000 + 11 が 10000 を法いくつになるかがわかれば、求めたい数を見つけることができます。もう一度、二項定理を使って
1122
= ( 10 + 1 )22
= 1022 + 22C1・1021 + ... + 22C19・103 + 22C20・102 + 22C21・10 + 1
≡ 22C3・1000 + 22C2・100 + 22C1・10 + 1 ( mod 10000 )
= ( 22・21・20 / 3・2 )・1000 + ( 22・21 / 2 )・100 + 220 + 1
= 1540000 + 23100 + 2201 + 1
≡ 3321 ( mod 10000 )
となり、
23・2000 + 11 = 46011 ≡ 6011 ( mod 10000 )
なので、
3321・6011 = 19962531 ≡ 2531 ( mod 10000 )
となって、求める数は 2531 となります。
2) オイラーの定理より、自然数 n と互いに素な数の個数を φ( n ) としたとき、整数 a と n が互いに素であれば、
aφ(n) ≡ 1 ( mod n )
が成り立ちます。n が素数の場合、φ(n) = n - 1 なので、これはフェルマーの小定理の一般化になります。φ(n) には以下の定理が成り立ちます。
素数 p に対し、
φ(p) = p - 1
φ(pm) = pm - pm-1
m, n が互いに素であれば
φ(mn) = φ(m)・φ(n)
以下の説明ではこれらを利用します。
10000 = 24・54 より
φ(10000)
= φ(24・54)
= φ(24)・φ(54)
= ( 24 - 23 )( 54 - 53 )
= ( 16 - 8 )( 625 - 125 ) = 8・500 = 4000 = 20・10・5・4
2011 と 10000 は互いに素なので、オイラーの定理から
201120・10・5・2 ≡ 1 ( mod 10000 )
となります。23! は 23 以下の全ての自然数の積なので、この結果から 201123! ≡ 1 ( mod 10000 ) となります。
-----
オイラーの定理は、フェルマーの小定理の場合とほぼ同じ方法で証明ができます。
まず、自然数 n と互いに素な自然数を bj ( j = 1, 2, ... φ(n) ) とします。bj の全てに、n と互いに素なある自然数 a を掛けた数 abj は、a, bj のどちらも n と互いに素であることから abj も n と互いに素であり、ある k ( k = 1, 2, ... φ(n) ) に対して
abj ≡ bk ( mod n )
が成り立ちます。なぜなら、n と互いに素で n 以下の数は φ(n) の bk の中にしか存在しないからです。二数 bj と bk について
abj ≡ abk ( mod n )
が成り立つと仮定した時、
a( bj - bk ) ≡ 0 ( mod n )
より a( bj - bk ) は n で割り切れます。しかし、a は n と互いに素なので、bj - bk が n で割り切れなければなりません。また、1 ≤ bj < n より | bj - bk | < n なので、条件を満たす数はゼロのみとなります。つまり、a を掛けたときに合同になる数が等しくなる bj は存在せず重複しないことから
abj ≡ bk ( mod n )
を満たす 1 から φ(n) までの全ての bk が存在することになります。すなわち
Πj{1→φ(n)}( abj ) ≡ Πk{1→φ(n)}( bk ) ( mod n )
であり、左辺は
Πj{1→φ(n)}( abj ) = aφ(n)Πj{1→φ(n)}( bj )
なので、両辺を Πj{1→φ(n)}( bj ) で割れば
aφ(n) ≡ 1 ( mod n )
となります。
-----
最後のところでさりげなく両辺を Πj{1→φ(n)}( bj ) で割りましたが、mc ≡ nc ( mod k ) のときに
m ≡ n ( mod k )
は必ずしも成り立つとは限りません。例えば、
30 ≡ 6 ( mod 8 )
は成り立ちますが、両辺を 2 で割った
15 ≡ 3 ( mod 8 )
は成り立ちません。しかし、c が k と互いに素であれば成り立ちます。bj は全て n と互いに素なので問題はないというわけです。
3 月に間に合わせる形で「アルゴリズムのコーナー」を更新しました。過去に公開した「ウェーブレット変換」の内容を見直しています。過去に作ったドキュメントをみると変な箇所や説明不足の部分もいろいろとあったのでかなり手直ししています。メインは多重解像度解析なのに、連続ウェーブレット変換の方が見直しに時間がかかりました。
そして、過去に拾ったまま放置していた問題を気合入れて解きました。ようやく暗算で計算できる方法を思いついたので紹介しておきます。
-----
1) 201123 の下 4 桁を求めよ。
2) 201123! の下 4 桁を求めよ ( cruz__F 様 )
以下、合同式を多用するので、先に定義といくつかの定理だけ示しておきます。
整数 m, k, q, r に対して m = qk + r となるとき、「m は k を法として r と合同である」といい、m ≡ r ( mod k ) と表します。これを「合同式」または「モジュラー演算」といいます。「時計算」と呼ばれることもあります。合同式では、m ≡ r ( mod k ) かつ n ≡ s ( mod k ) であるとき、
m ± n ≡ r ± s ( mod k )
m・n ≡ r・s ( mod k )
mn ≡ rn ( mod k )
が成り立ちます。
1) 二項定理より
201123
= ( 2000 + 11 )23
= 200023 + 23C1・200022・11 + ... + 23C22・2000・1122 + 1123
≡ 23・2000・1122 + 1123 ( mod 10000 )
となります。なぜなら、任意のゼロでない自然数 N と 1 より大きい自然数 a に対し、2000a・N ≡ 0 ( mod 10000 ) となるため、そのような項は無視できるからです。
23・2000・1122 + 1123 = 1122( 23・2000 + 11 )
より、1122 と 23・2000 + 11 が 10000 を法いくつになるかがわかれば、求めたい数を見つけることができます。もう一度、二項定理を使って
1122
= ( 10 + 1 )22
= 1022 + 22C1・1021 + ... + 22C19・103 + 22C20・102 + 22C21・10 + 1
≡ 22C3・1000 + 22C2・100 + 22C1・10 + 1 ( mod 10000 )
= ( 22・21・20 / 3・2 )・1000 + ( 22・21 / 2 )・100 + 220 + 1
= 1540000 + 23100 + 2201 + 1
≡ 3321 ( mod 10000 )
となり、
23・2000 + 11 = 46011 ≡ 6011 ( mod 10000 )
なので、
3321・6011 = 19962531 ≡ 2531 ( mod 10000 )
となって、求める数は 2531 となります。
2) オイラーの定理より、自然数 n と互いに素な数の個数を φ( n ) としたとき、整数 a と n が互いに素であれば、
aφ(n) ≡ 1 ( mod n )
が成り立ちます。n が素数の場合、φ(n) = n - 1 なので、これはフェルマーの小定理の一般化になります。φ(n) には以下の定理が成り立ちます。
素数 p に対し、
φ(p) = p - 1
φ(pm) = pm - pm-1
m, n が互いに素であれば
φ(mn) = φ(m)・φ(n)
以下の説明ではこれらを利用します。
10000 = 24・54 より
φ(10000)
= φ(24・54)
= φ(24)・φ(54)
= ( 24 - 23 )( 54 - 53 )
= ( 16 - 8 )( 625 - 125 ) = 8・500 = 4000 = 20・10・5・4
2011 と 10000 は互いに素なので、オイラーの定理から
201120・10・5・2 ≡ 1 ( mod 10000 )
となります。23! は 23 以下の全ての自然数の積なので、この結果から 201123! ≡ 1 ( mod 10000 ) となります。
-----
オイラーの定理は、フェルマーの小定理の場合とほぼ同じ方法で証明ができます。
まず、自然数 n と互いに素な自然数を bj ( j = 1, 2, ... φ(n) ) とします。bj の全てに、n と互いに素なある自然数 a を掛けた数 abj は、a, bj のどちらも n と互いに素であることから abj も n と互いに素であり、ある k ( k = 1, 2, ... φ(n) ) に対して
abj ≡ bk ( mod n )
が成り立ちます。なぜなら、n と互いに素で n 以下の数は φ(n) の bk の中にしか存在しないからです。二数 bj と bk について
abj ≡ abk ( mod n )
が成り立つと仮定した時、
a( bj - bk ) ≡ 0 ( mod n )
より a( bj - bk ) は n で割り切れます。しかし、a は n と互いに素なので、bj - bk が n で割り切れなければなりません。また、1 ≤ bj < n より | bj - bk | < n なので、条件を満たす数はゼロのみとなります。つまり、a を掛けたときに合同になる数が等しくなる bj は存在せず重複しないことから
abj ≡ bk ( mod n )
を満たす 1 から φ(n) までの全ての bk が存在することになります。すなわち
Πj{1→φ(n)}( abj ) ≡ Πk{1→φ(n)}( bk ) ( mod n )
であり、左辺は
Πj{1→φ(n)}( abj ) = aφ(n)Πj{1→φ(n)}( bj )
なので、両辺を Πj{1→φ(n)}( bj ) で割れば
aφ(n) ≡ 1 ( mod n )
となります。
-----
最後のところでさりげなく両辺を Πj{1→φ(n)}( bj ) で割りましたが、mc ≡ nc ( mod k ) のときに
m ≡ n ( mod k )
は必ずしも成り立つとは限りません。例えば、
30 ≡ 6 ( mod 8 )
は成り立ちますが、両辺を 2 で割った
15 ≡ 3 ( mod 8 )
は成り立ちません。しかし、c が k と互いに素であれば成り立ちます。bj は全て n と互いに素なので問題はないというわけです。
2016年03月27日
早朝の月
昨日は 5 時に起床しました。
空はまだ真っ暗でしたが、月がキレイだったので撮影してみました。撮影すると何となくショボくなりますね。

そして今日は日曜日ですが、5 時半に目が覚めてしまいました。空はだいぶ明るくなっていましたが、まだ月は見えていたのでまたカメラで撮影。

こうやって見ると、月の満ち欠けって結構早いんですね。それにしても、明け方はまだ寒いです。
「数学問題bot(個人用)」から今回は東大の入試問題にチャレンジ。なぜか最初の問題で大苦戦して何日間か悩んでいました。なお、合っている保証なしです。
-----
p, q は実数の定数で、0 < p < 1, q > 0 を満たすとする。関数
f(x) = ( 1 - p )x + ( 1 - x )( 1 - e-qx )
を考える。
以下の問いに答えよ。必要であれば、不等式 1 + x ≤ ex が全ての実数 x に対して成り立つことを証明なしに用いてよい。
(1) 0 < x < 1 のとき、0 < f(x) < 1 であることを示せ。
(2) x0 は 0 < x0 < 1 を満たす実数とする。数列 {xn} の各項 xn ( n = 1, 2, ... ) を、
xn = f(xn-1)
によって順次定める。p > q であるとき、
lim{n→∞} xn = 0
となることを示せ。
(3) p < q であるとき、
c = f(c), 0 < c < 1
を満たす実数 c が存在することを示せ。
(東京大・2014・前・理)
-----
(1) f(x) の変数を q として f(q) の軌跡を考えます。
f(0) = ( 1 - p )x で 0 < 1 - p < 1 かつ 0 < x < 1 なので 0 < f(0) < 1 となります。
また、q → ∞ のとき f(q) → ( 1 - p )x + ( 1 - x ) = 1 - px なのでやはり 0 < lim{q→∞} f(q) < 1 となります。
f'(q) = q( 1 - x )e-qx で q > 0 より任意の q に対して f'(q) > 0 となり、f(q) は単調増加となります。従って、命題が成り立ちます。
(2) (1) より、0 < x0 < 1 ならば任意の n に対して 0 < xn < 1 が成り立ちます。
1 - qx ≤ e-qx より 1 - e-qx ≤ qx なので、xn = f(xn-1) ≤ ( 1 - p )xn-1 + qxn-1( 1 - xn-1 ) が成り立ち、
xn-1 - xn ≥ xn-1 - [ ( 1 - p )xn-1 + qxn-1( 1 - xn-1 ) ]
= xn-1( p - q + qxn-1 )
より p > q ならば xn-1 - xn > 0 となるので { xn } は単調減少となります。f(0) = 0 であることから { xn } は必ず 0 に収束し、lim{n→∞} xn = 0 が成り立ちます。
(3) g(x) = f(x) - x とします。このとき、
g(x) = -px + ( 1 - x )( 1 - e-qx )
なので、g(0) = 0、g(1) = -p < 0 となります。従って、g'(0) > 0 になるなら、0 < c < 1 かつ g(0) = 0 を満たす実数 c が存在します。
g'(x) = -p - ( 1 - e-qx ) + qe-qx( 1 - x ) より g'(0) = -p + q なので、p ≤ q ならば g'(0) > 0 です。従って、g(0) = c を満たす実数 c が存在し、f(c) = g(c) + c = c より命題が成り立ちます。
空はまだ真っ暗でしたが、月がキレイだったので撮影してみました。撮影すると何となくショボくなりますね。

そして今日は日曜日ですが、5 時半に目が覚めてしまいました。空はだいぶ明るくなっていましたが、まだ月は見えていたのでまたカメラで撮影。

こうやって見ると、月の満ち欠けって結構早いんですね。それにしても、明け方はまだ寒いです。
「数学問題bot(個人用)」から今回は東大の入試問題にチャレンジ。なぜか最初の問題で大苦戦して何日間か悩んでいました。なお、合っている保証なしです。
-----
p, q は実数の定数で、0 < p < 1, q > 0 を満たすとする。関数
f(x) = ( 1 - p )x + ( 1 - x )( 1 - e-qx )
を考える。
以下の問いに答えよ。必要であれば、不等式 1 + x ≤ ex が全ての実数 x に対して成り立つことを証明なしに用いてよい。
(1) 0 < x < 1 のとき、0 < f(x) < 1 であることを示せ。
(2) x0 は 0 < x0 < 1 を満たす実数とする。数列 {xn} の各項 xn ( n = 1, 2, ... ) を、
xn = f(xn-1)
によって順次定める。p > q であるとき、
lim{n→∞} xn = 0
となることを示せ。
(3) p < q であるとき、
c = f(c), 0 < c < 1
を満たす実数 c が存在することを示せ。
(東京大・2014・前・理)
-----
(1) f(x) の変数を q として f(q) の軌跡を考えます。
f(0) = ( 1 - p )x で 0 < 1 - p < 1 かつ 0 < x < 1 なので 0 < f(0) < 1 となります。
また、q → ∞ のとき f(q) → ( 1 - p )x + ( 1 - x ) = 1 - px なのでやはり 0 < lim{q→∞} f(q) < 1 となります。
f'(q) = q( 1 - x )e-qx で q > 0 より任意の q に対して f'(q) > 0 となり、f(q) は単調増加となります。従って、命題が成り立ちます。
(2) (1) より、0 < x0 < 1 ならば任意の n に対して 0 < xn < 1 が成り立ちます。
1 - qx ≤ e-qx より 1 - e-qx ≤ qx なので、xn = f(xn-1) ≤ ( 1 - p )xn-1 + qxn-1( 1 - xn-1 ) が成り立ち、
xn-1 - xn ≥ xn-1 - [ ( 1 - p )xn-1 + qxn-1( 1 - xn-1 ) ]
= xn-1( p - q + qxn-1 )
より p > q ならば xn-1 - xn > 0 となるので { xn } は単調減少となります。f(0) = 0 であることから { xn } は必ず 0 に収束し、lim{n→∞} xn = 0 が成り立ちます。
(3) g(x) = f(x) - x とします。このとき、
g(x) = -px + ( 1 - x )( 1 - e-qx )
なので、g(0) = 0、g(1) = -p < 0 となります。従って、g'(0) > 0 になるなら、0 < c < 1 かつ g(0) = 0 を満たす実数 c が存在します。
g'(x) = -p - ( 1 - e-qx ) + qe-qx( 1 - x ) より g'(0) = -p + q なので、p ≤ q ならば g'(0) > 0 です。従って、g(0) = c を満たす実数 c が存在し、f(c) = g(c) + c = c より命題が成り立ちます。
2016年03月26日
はちみつ
美味しいはちみつを求めて、通販限定のお試しセットを買ってみました。
いくつかある中で、フランス産のラベンダーはちみつがなかなかにおいしかったので追加で購入しました。パンやヨーグルトにかけて使ってます。それにしても、花の種類によって味や食感も様々ですね。モカコーヒーのはちみつはにおいにかなり癖があってちょっと無理でした。あと試していないのはそばのはちみつですが、これもいつか食べてみたいです。はちみつを使った簡単なレシピがあればそれも試してみたいですね。
「数学問題bot(個人用)」から昔に拾った問題を解いてみました。合っている保証なしです。
-----
4 つの正数 a, b, c, d について a = b = c = d でないならば、4 つの数 a( 1 - b ), b( 1 - c ), c( 1 - d ), d( 1 - a ) のうち少なくとも 1 つは 1 / 4 より小さいことを証明せよ ( 1978 年東京理科大 )
まず、4 つの数が 1 / 4 以上だと仮定します。このとき、a( 1 - b ) ≥ 1 / 4 > 0 で a > 0 なので、1 - b > 0 となり、0 < b < 1 が成り立ちます。
同様に他の数 a, c, d についてもこれは成り立ちます。
4 つの数の和を計算すると、
a( 1 - b ) + b( 1 - c ) + c( 1 - d ) + d( 1 - a )
= ( a + b + c + d ) - ( ab + bc + cd + da )
= ( a + c ) + ( b + d ) - ( a + c )( b + d )
= ( a + c - 1 )( 1 - b - d ) + 1
で、これは仮定より 1 以上となるので、
( a + c - 1 )( b + d - 1 ) ≤ 0
が成り立ちます。これが成り立つためには、
i) a + c ≤ 1 かつ b + d ≥ 1
ii) a + c ≥ 1 かつ b + d ≤ 1
のいずれかを条件として満たす必要があります。i) のときは、a ≤ 1 - c かつ 1 - b ≤ d なので、設問の前提条件も併せれば
1 / 4 ≤ a( 1 - b ) ≤ d( 1 - c )
となります。また、c ≤ 1 - a かつ 1 - d ≤ b とも変形できるため、
1 / 4 ≤ c( 1 - d ) ≤ b( 1 - a )
ともなります。1 / 4 ≤ b( 1 - a ) より b ≥ 1 / 4( 1 - a ) を 1 / 4 ≤ a( 1 - b ) に適用して
1 / 4 ≤ a( 1 - b ) ≤ a[ 1 - 1 / 4( 1 - a ) ]
1 - a > より両辺に 4( 1 - a ) を掛ければ
1 - a ≤ a[ 4( 1 - a ) - 1 ] = -4a2 + 3a
式を整理して 4a2 - 4a + 1 ≤ 0 より ( 2a - 1 )2 ≤ 0 なので、これを満たす実数は 1 / 2 しかありません。
このとき、1 / 4 ≤ ( 1- b ) / 2 かつ 1 / 4 ≤ b / 2 が成り立つ必要があるので b = 1 / 2 になります。さらに、ii) の条件から同様の手順で c = d = 1 / 2 となり、a = b = c = d = 1 / 2 となります。
従って、その対偶である設問の命題が証明されました。
いくつかある中で、フランス産のラベンダーはちみつがなかなかにおいしかったので追加で購入しました。パンやヨーグルトにかけて使ってます。それにしても、花の種類によって味や食感も様々ですね。モカコーヒーのはちみつはにおいにかなり癖があってちょっと無理でした。あと試していないのはそばのはちみつですが、これもいつか食べてみたいです。はちみつを使った簡単なレシピがあればそれも試してみたいですね。
「数学問題bot(個人用)」から昔に拾った問題を解いてみました。合っている保証なしです。
-----
4 つの正数 a, b, c, d について a = b = c = d でないならば、4 つの数 a( 1 - b ), b( 1 - c ), c( 1 - d ), d( 1 - a ) のうち少なくとも 1 つは 1 / 4 より小さいことを証明せよ ( 1978 年東京理科大 )
まず、4 つの数が 1 / 4 以上だと仮定します。このとき、a( 1 - b ) ≥ 1 / 4 > 0 で a > 0 なので、1 - b > 0 となり、0 < b < 1 が成り立ちます。
同様に他の数 a, c, d についてもこれは成り立ちます。
4 つの数の和を計算すると、
a( 1 - b ) + b( 1 - c ) + c( 1 - d ) + d( 1 - a )
= ( a + b + c + d ) - ( ab + bc + cd + da )
= ( a + c ) + ( b + d ) - ( a + c )( b + d )
= ( a + c - 1 )( 1 - b - d ) + 1
で、これは仮定より 1 以上となるので、
( a + c - 1 )( b + d - 1 ) ≤ 0
が成り立ちます。これが成り立つためには、
i) a + c ≤ 1 かつ b + d ≥ 1
ii) a + c ≥ 1 かつ b + d ≤ 1
のいずれかを条件として満たす必要があります。i) のときは、a ≤ 1 - c かつ 1 - b ≤ d なので、設問の前提条件も併せれば
1 / 4 ≤ a( 1 - b ) ≤ d( 1 - c )
となります。また、c ≤ 1 - a かつ 1 - d ≤ b とも変形できるため、
1 / 4 ≤ c( 1 - d ) ≤ b( 1 - a )
ともなります。1 / 4 ≤ b( 1 - a ) より b ≥ 1 / 4( 1 - a ) を 1 / 4 ≤ a( 1 - b ) に適用して
1 / 4 ≤ a( 1 - b ) ≤ a[ 1 - 1 / 4( 1 - a ) ]
1 - a > より両辺に 4( 1 - a ) を掛ければ
1 - a ≤ a[ 4( 1 - a ) - 1 ] = -4a2 + 3a
式を整理して 4a2 - 4a + 1 ≤ 0 より ( 2a - 1 )2 ≤ 0 なので、これを満たす実数は 1 / 2 しかありません。
このとき、1 / 4 ≤ ( 1- b ) / 2 かつ 1 / 4 ≤ b / 2 が成り立つ必要があるので b = 1 / 2 になります。さらに、ii) の条件から同様の手順で c = d = 1 / 2 となり、a = b = c = d = 1 / 2 となります。
従って、その対偶である設問の命題が証明されました。
2016年03月21日
名大問題 2016 (6)
連休中はずっと外出していたわけですが、桜はまだのようです。
しかし、ソメイヨシノ以外の桜で咲いていたのを近所の公園で見つけたのでカメラで撮っておきました。

もう、葉が見えてしまっているということは、花も落ち始めているのかな。
最後の名古屋大入試問題。最後におまけも付けてあります。例によって合っている保証はありません。
-----
正の n に対して、その ( 1 と自分自身も含めた ) すべての正の約数の和を s(n) と書くことにする。このとき、次の問に答えよ。
(1) k を正の整数、p を 3 以上の素数とするとき、s(2kp) を求めよ。
(2) s(2016) を求めよ。
(3) 2016 の正の約数 n で、s(n) = 2016 となるものをすべて求めよ。
(1) 2kp の約数は、
1, 2, 22, ... 2k
p, 2p, 22p, ... 2kp
なので、
s(2kp)
= Σj{0→k}( 2j ) + Σj{0→k}( 2jp )
= Σj{0→k}( 2j( p + 1 ) )
= ( 2k+1 - 1 )( p + 1 )
となります。
(2) 2016 = 25・32・7 より、約数は
です。これをマジメに足しあわせて
s(2016)
= Σj{0→5}( 2j( 1 + 3 + 32 + 7 + 3・7 + 32・7 ) )
= ( 26 - 1 )・104
= 63・104 = 6552
となります。
(3) m の約数の和を s(m) としたとき、s(m) に対して、s( 2km ) は (1)(2) の結果から ( 2k+1 - 1 )s(m) となることがわかります。2016 = 25・32・7 より、s(n) = 2016 となる n を求めるには ( 26 - 1 )s(m) = 2016 を満たす m を見つければよいことになります。s(m) = 2016 / 63 = 32 なので、約数の和が 32 以下の数を n の中から調べると
s(1) = 1 s(3) = 4 s(32) = 13 s(7) = 8 s(3・7) = 32
となって、3・7 が一つ見つかりました。残りの約数は全て上記 5 つの数に 2k ( 1 ≤ k ≤ 5 ) を掛けあわせることで得られますが、その約数の和は上記で求めた約数の和に 2k+1 - 1 を掛けた数に等しくなり、この数が奇数であることから 32 になるためには s(m) が偶数でなければなりません。それは s(3) と s(7) で、
s(2・3) = 12 s(2・3) = 28 でこれより大きな数は 32 より大きくなるため該当するものはなく、
s(2・7) = 24 でこれより大きな数は 32 より大きくなるためこちらも該当するものはありません。
従って、求める数は 25・3・7 = 672 となります。
-----
約数の和 s(n) にはおもしろい性質があります。素数 p の約数は 1 と p だけなので、s(p) = p + 1 です。また、p のべき乗 pm の約数は 1, p, p2, ... pm であり、
s(pm) = Σj{0→m}( pj ) = ( pm+1 - ) / ( p - 1 )
となります。二つの素数の積 pq の約数は 1, p, q, pq であり、
s(pq) = 1 + p + q + pq = ( p + 1 )( q + 1 ) = s(p)s(q)
となり、さらに pmqn の約数は 0 ≤ j ≤ m, 0 ≤ k ≤ n を満たす任意の整数について pjqk で表わされるので、
s(pmqn)
= Σj{0→m}( Σk{0→n}( pjqk ) )
= Σj{0→m}( pjΣk{0→n}( qk ) )
= Σj{0→m}( pjs(qn) )
= s(pm)s(qn)
となります。この結果は一般化して
s( Πk( pkmk ) ) = Πk( s( pkmk ) )
となるので、もし m と n が共通の素因数を持たない、つまり互いに素であれば
s(mn) = s(m)・s(n)
が成り立ちます。
しかし、ソメイヨシノ以外の桜で咲いていたのを近所の公園で見つけたのでカメラで撮っておきました。

もう、葉が見えてしまっているということは、花も落ち始めているのかな。
最後の名古屋大入試問題。最後におまけも付けてあります。例によって合っている保証はありません。
-----
正の n に対して、その ( 1 と自分自身も含めた ) すべての正の約数の和を s(n) と書くことにする。このとき、次の問に答えよ。
(1) k を正の整数、p を 3 以上の素数とするとき、s(2kp) を求めよ。
(2) s(2016) を求めよ。
(3) 2016 の正の約数 n で、s(n) = 2016 となるものをすべて求めよ。
(1) 2kp の約数は、
1, 2, 22, ... 2k
p, 2p, 22p, ... 2kp
なので、
s(2kp)
= Σj{0→k}( 2j ) + Σj{0→k}( 2jp )
= Σj{0→k}( 2j( p + 1 ) )
= ( 2k+1 - 1 )( p + 1 )
となります。
(2) 2016 = 25・32・7 より、約数は
| 1 | 2 | 22 | 23 | 24 | 25 |
| 3 | 2・3 | 22・3 | 23・3 | 24・3 | 25・3 |
| 32 | 2・32 | 22・32 | 23・32 | 24・32 | 25・32 |
| 7 | 2・7 | 22・7 | 23・7 | 24・7 | 25・7 |
| 3・7 | 2・3・7 | 22・3・7 | 23・3・7 | 24・3・7 | 25・3・7 |
| 32・7 | 2・32・7 | 22・32・7 | 23・32・7 | 24・32・7 | 25・32・7 |
です。これをマジメに足しあわせて
s(2016)
= Σj{0→5}( 2j( 1 + 3 + 32 + 7 + 3・7 + 32・7 ) )
= ( 26 - 1 )・104
= 63・104 = 6552
となります。
(3) m の約数の和を s(m) としたとき、s(m) に対して、s( 2km ) は (1)(2) の結果から ( 2k+1 - 1 )s(m) となることがわかります。2016 = 25・32・7 より、s(n) = 2016 となる n を求めるには ( 26 - 1 )s(m) = 2016 を満たす m を見つければよいことになります。s(m) = 2016 / 63 = 32 なので、約数の和が 32 以下の数を n の中から調べると
s(1) = 1 s(3) = 4 s(32) = 13 s(7) = 8 s(3・7) = 32
となって、3・7 が一つ見つかりました。残りの約数は全て上記 5 つの数に 2k ( 1 ≤ k ≤ 5 ) を掛けあわせることで得られますが、その約数の和は上記で求めた約数の和に 2k+1 - 1 を掛けた数に等しくなり、この数が奇数であることから 32 になるためには s(m) が偶数でなければなりません。それは s(3) と s(7) で、
s(2・3) = 12 s(2
s(2・7) = 24 でこれより大きな数は 32 より大きくなるためこちらも該当するものはありません。
従って、求める数は 25・3・7 = 672 となります。
-----
約数の和 s(n) にはおもしろい性質があります。素数 p の約数は 1 と p だけなので、s(p) = p + 1 です。また、p のべき乗 pm の約数は 1, p, p2, ... pm であり、
s(pm) = Σj{0→m}( pj ) = ( pm+1 - ) / ( p - 1 )
となります。二つの素数の積 pq の約数は 1, p, q, pq であり、
s(pq) = 1 + p + q + pq = ( p + 1 )( q + 1 ) = s(p)s(q)
となり、さらに pmqn の約数は 0 ≤ j ≤ m, 0 ≤ k ≤ n を満たす任意の整数について pjqk で表わされるので、
s(pmqn)
= Σj{0→m}( Σk{0→n}( pjqk ) )
= Σj{0→m}( pjΣk{0→n}( qk ) )
= Σj{0→m}( pjs(qn) )
= s(pm)s(qn)
となります。この結果は一般化して
s( Πk( pkmk ) ) = Πk( s( pkmk ) )
となるので、もし m と n が共通の素因数を持たない、つまり互いに素であれば
s(mn) = s(m)・s(n)
が成り立ちます。





