2016年03月20日
名大問題 2016 (5)
今日は風の強い日ですね。
今更ながら God of War 2 のタイタンモードに挑戦しています。かなり昔にテセウス戦までは何とかクリアして、バーバリアン・キング前でやめてしまっていました。ちょっとやってみようかと思い、苦戦の末、バーバリアン・キングとエウリュアレまで何とか倒して、ロック・ミノタウロス + ハーピー極悪コンビに倒されまくってます。時間のあるときに少しずつ進めようと考えてます。このゲーム、イージーやノーマルなら戦闘は苦戦することなく、逆に謎解きが大変でした。ハード以降はガラリと変わり、戦闘が非常にきついです。特にタイタンモードはハードすら楽に思えるくらいきつく、何度死んだかわかりません。でも、攻略法などを参考にすればアクションが下手でも何とか進められます。後半はどうなるかわかりませんが。昔のゲームですが、今でもベストゲームの一つです。
今年の名古屋大入試から、今回は文系の問題です。なぜか個人的には文系の問題の方に苦戦しました。例によって合っている保証なしです。
-----
n を正の整数とし、k を 1 ≤ k ≤ n + 2 を満たす整数とする。n + 2 枚のカードがあり、そのうちの 1 枚には数字 0 が、他の 1 枚には数字 2 が、残りの n 枚には数字 1 が書かれている。この n + 2 枚のカードのうちから無作為に k 枚のカードを取り出すとする。このとき、次の問に答えよ。
(1) 取り出した k 枚のカードに書かれているすべての数字の積が 1 以上になる確率を求めよ。
(2) 取り出した k 枚のカードに書かれているすべての数字の積が 2 となる確率 Qn(k) を求めよ。
(3) 与えられた n に対して、確率 Qn(k) が最大となる k の値と、その最大値を求めよ。
(1) 積が 0 になるのは、0 のカードが k 枚の中に含まれた時で、その確率は
1 / ( n + 2 ) + [ ( n + 1 )( n + 2 ) ]・[ 1 / ( n + 1 ) ] + ... + [ ( n + 1 ) / ( n + 2 ) ]・[ n / ( n + 1 ) ]・ ... ・[ 1 / ( n - k + 3 ) ] = k / ( n + 2 )
となるので、その余事象である 1 以上となる確率は
1 - k ( n + 2 ) = ( n - k + 2 ) / ( n + 2 )
となります。
(2) 1 のカードだけが含まれる確率は、n + 2 枚のカードから k 枚を選択する場合の数 n+2Ck で、0, 1 を除いた n 枚のカードから k 枚を選択する場合の数 nCk で割った値で、
nCk / n+2Ck
= [ n! / k!・( n - k )! ] / [ ( n + 2 )! / k!・( n + 2 - k )! ]
= ( n - k + 2 )( n - k + 1 ) / ( n + 1 )( n + 2 )
となります。数字の積が 2 となるのは、1 以上になる事象から 1 になる事象、すなわち 1 のカードのみを含んだ事象を除けばよいので、
Qn(k) = ( n - k + 2 ) / ( n + 2 ) - ( n - k + 2 )( n - k + 1 ) / ( n + 1 )( n + 2 ) = k( n - k +2 ) / ( n + 1 )( n + 2 )
となります。
(3) n は定数なので、f(k) = k( n - k +2 ) の最大値を求めれば十分です。
f(k) = -[ k - ( n + 2 ) / 2 ]2 + ( n + 2 )2 / 4 より、f(k) は k = ( n + 2 ) / 2 のとき最大となります。
n が偶数なら k = ( n + 2 ) / 2 のとき最大で、Qn(k) = [ ( n + 2 )2 / 4 ] / ( n + 1 )( n + 2 ) = ( n + 2 ) / 4( n + 1 )
n が奇数なら k = ( n + 1 ) / 2, ( n + 3 ) / 2 のとき最大で、
Qn(k) = [ ( n + 1 )( n + 3 ) / 4 ] / ( n + 1 )( n + 2 ) = ( n + 3 ) / 4( n + 2 )
となります。
今更ながら God of War 2 のタイタンモードに挑戦しています。かなり昔にテセウス戦までは何とかクリアして、バーバリアン・キング前でやめてしまっていました。ちょっとやってみようかと思い、苦戦の末、バーバリアン・キングとエウリュアレまで何とか倒して、ロック・ミノタウロス + ハーピー極悪コンビに倒されまくってます。時間のあるときに少しずつ進めようと考えてます。このゲーム、イージーやノーマルなら戦闘は苦戦することなく、逆に謎解きが大変でした。ハード以降はガラリと変わり、戦闘が非常にきついです。特にタイタンモードはハードすら楽に思えるくらいきつく、何度死んだかわかりません。でも、攻略法などを参考にすればアクションが下手でも何とか進められます。後半はどうなるかわかりませんが。昔のゲームですが、今でもベストゲームの一つです。
今年の名古屋大入試から、今回は文系の問題です。なぜか個人的には文系の問題の方に苦戦しました。例によって合っている保証なしです。
-----
n を正の整数とし、k を 1 ≤ k ≤ n + 2 を満たす整数とする。n + 2 枚のカードがあり、そのうちの 1 枚には数字 0 が、他の 1 枚には数字 2 が、残りの n 枚には数字 1 が書かれている。この n + 2 枚のカードのうちから無作為に k 枚のカードを取り出すとする。このとき、次の問に答えよ。
(1) 取り出した k 枚のカードに書かれているすべての数字の積が 1 以上になる確率を求めよ。
(2) 取り出した k 枚のカードに書かれているすべての数字の積が 2 となる確率 Qn(k) を求めよ。
(3) 与えられた n に対して、確率 Qn(k) が最大となる k の値と、その最大値を求めよ。
(1) 積が 0 になるのは、0 のカードが k 枚の中に含まれた時で、その確率は
1 / ( n + 2 ) + [ ( n + 1 )( n + 2 ) ]・[ 1 / ( n + 1 ) ] + ... + [ ( n + 1 ) / ( n + 2 ) ]・[ n / ( n + 1 ) ]・ ... ・[ 1 / ( n - k + 3 ) ] = k / ( n + 2 )
となるので、その余事象である 1 以上となる確率は
1 - k ( n + 2 ) = ( n - k + 2 ) / ( n + 2 )
となります。
(2) 1 のカードだけが含まれる確率は、n + 2 枚のカードから k 枚を選択する場合の数 n+2Ck で、0, 1 を除いた n 枚のカードから k 枚を選択する場合の数 nCk で割った値で、
nCk / n+2Ck
= [ n! / k!・( n - k )! ] / [ ( n + 2 )! / k!・( n + 2 - k )! ]
= ( n - k + 2 )( n - k + 1 ) / ( n + 1 )( n + 2 )
となります。数字の積が 2 となるのは、1 以上になる事象から 1 になる事象、すなわち 1 のカードのみを含んだ事象を除けばよいので、
Qn(k) = ( n - k + 2 ) / ( n + 2 ) - ( n - k + 2 )( n - k + 1 ) / ( n + 1 )( n + 2 ) = k( n - k +2 ) / ( n + 1 )( n + 2 )
となります。
(3) n は定数なので、f(k) = k( n - k +2 ) の最大値を求めれば十分です。
f(k) = -[ k - ( n + 2 ) / 2 ]2 + ( n + 2 )2 / 4 より、f(k) は k = ( n + 2 ) / 2 のとき最大となります。
n が偶数なら k = ( n + 2 ) / 2 のとき最大で、Qn(k) = [ ( n + 2 )2 / 4 ] / ( n + 1 )( n + 2 ) = ( n + 2 ) / 4( n + 1 )
n が奇数なら k = ( n + 1 ) / 2, ( n + 3 ) / 2 のとき最大で、
Qn(k) = [ ( n + 1 )( n + 3 ) / 4 ] / ( n + 1 )( n + 2 ) = ( n + 3 ) / 4( n + 2 )
となります。
2016年03月17日
名大問題 2016 (4)
昼からは暖かい一日でした。夜も寒くないというのは久しぶりのような気がします。
丸善出版の「パターン認識と機械学習」という書籍があります。以前、上巻だけを購入して読み進めていました。上巻は 6,500 円と高価でしたが、下巻はさらに高く 7,800 円もします。買うのはずっとためらっていたものの、上巻もだいぶ読み進めたので、本屋に立ち寄ったときに衝動買いしてしまいました。まだ上巻の残りを読んでいるところなので、もう少ししてから読もうと考えています。パターン認識関連の書籍はいろいろと買いましたが、高価なだけにこの本が一番まとまっている上に説明もある程度は細かく書かれていると思います。しかし、全部理解するにはあと 2, 3 冊、統計関係の書籍は必要になります。読むだけでもかなり苦労しました。
いい本だと思うので、図書館などにあれば借りて読むというのもオススメです。
2016 年名古屋大入試の理系最後の問題です。まだ、文系問題がふたつ残ってます。例によって合っている保証はありません。
-----
次の問に答えよ。ただし 2 次方程式の重解は 2 つと数える。
(1) 次の条件 (*) を満たす整数 a, b, c, d, e, f の組をすべて求めよ。
(*)
・2 次方程式 x2 + ax + b = 0 の 2 つの解が c, d である。
・2 次方程式 x2 + cx + d = 0 の 2 つの解が e, f である。
・2 次方程式 x2 + ex + f = 0 の 2 つの解が a, b である。
(2) 2 つの数列 { an }, { bn } は、次の条件 (**) を満たすものとする。
(**) すべての正の整数 n について、an, bn は整数であり、2 次方程式 x2 + anx + bn = 0 の 2 つの解が an+1, bn+1 である。
このとき、
(i) 正の整数 m で、| bm | = | bm+1 | = | bm+2 | = ... となるものが存在することを示せ。
(ii) 条件 (**) を満たす数列 { an }, { bn } の組をすべて求めよ。
(1) 二次方程式の解と係数の関係から
a = -c - d --- (a)
b = cd --- (b)
c = -e - f --- (c)
d = ef --- (d)
e = -a - b --- (e)
f = ab --- (f)
が成り立ちます。(b) を (f) に代入して f = acd、さらに (d) を代入すれば f = acef になります。
f ≠ 0 のとき、ace = 1 であり、これを満たす整数は a, c, e が全て 1 か、ひとつが 1 で残りが -1 の場合のみです。また、f ≠ 0 なので (b)(d) から b ≠ 0, d ≠ 0 となります。
(a) + (c) + (e) より
a + c + e = -( a + b + c + d + e + f )
2( a + c + e ) = -( b + d + f )
となるので、a = c = e = 1 なら b + d + f = -6 であり、(b)(d)(f) から b = d = f になります。
従って、この場合は { a, b, c, d, e, f } = { 1, -2, 1, -2, 1, -2 } です。
a = c = -1, e = 1 の場合、(a)(c)(e) より b = 0, d = 2, f = 0 となり、f ≠ 0 に反します。対称性から c = e = -1 かつ a = 1 の場合と e = a = -1 かつ c = 1 の場合も b, d, f のいずれかにゼロを含むため仮定に反します。
f = 0 のとき、(d) より d = 0, (b) より b = 0 となり、(a)(c)(e) より a = -c, c = -e, e = -a なので
a = -c = e = -a
となります。これを満たすのは a = 0 のときしかありません。対称性から同様に c = 0, e = 0 となるので、{ a, b, c, d, e, f } = { 0, 0, 0, 0, 0, 0 } となります。組はこの二つとなります。
(2)(i) 二次方程式の解と係数の関係から
am = -am+1 - bm+1 --- (a)
bm = am+1bm+1 --- (b)
が成り立つので、(b) より
bm = am+1bm+1 = am+1am+2bm+2 = ...
となります。任意の k > m に対して ak ≠ 0 ならば
bm / bm+1 = am+1
bm / bm+2 = am+1am+2
:
となるので、bm に対して bm+1 以降は全て約数とならなければなりません。また、
|am+1| ≤ |am+1am+2| ≤ ...
より
|bm / bm+1| ≤ |bm / bm+2| ≤ ...
なので
|bm+1| ≥ |bm+2| ≥ ...
となって、正の整数は有限なので必ずある値に収束します。最後に、am+1 = 0 となったとき、(b) より bm = 0 で、(b) の添字を一つ前にずらすと
bm-1 = ambm
なので bm-1 = 0 です。つまり、0 = b1 = b2= ... でありこの場合も成り立ちます。よて、命題が成り立つことが証明されました。
(2)(ii) (i) で証明した状態になったとき、(b) より bm ≠ 0 なら am はすべて ±1 となります。(a) にこの値を代入することで ( am, bm ) は ( bm ≠ 0 であることに注意して )
( am, bm ) = ( 1, -2 ), ( -1, 2 )
の二通りが得られます。( am, bm ) は解を ( am+1, bm+1 ) とする二次方程式の係数だったので、( 1, -2 ) のときは
x2 + x - 2 = 0
の解が ( am+1, bm+1 ) になります。その解は x = 1, -2 で、| am | = 1 という条件を満たすのは ( am+1, bm+1 ) = ( 1, -2 ) です。逆に、( am+1, bm+1 ) = ( 1, -2 ) なら (a)(b) より
am = -1 - ( -2 ) = 1
bm = 1・( -2 ) = -2
なので、全ての m に対して ( am, bm ) = ( 1, -2 ) ということになります。
( -1, 2 ) のときは
x2 - x + 2 = 0
の解が ( am+1, bm+1 ) になりますが、この方程式は整数解はおろか実数解もないので除外できます。
最後に、m がある値以上になったときに bm = 0 なら(a) より am = -am+1 なので、以降の am は絶対値の等しい値が符号だけ変化しながら続くことになります。その値を N としたとき、( am+1, bm+1 ) = ( N, 0 ) なら (a)(b) より
am = -N - 0 = -N
bm = N・0 = 0
であり、その前についても符号だけ変わって絶対値は変わりません。よって、任意の整数 N について { am } = { N, -N, N, ... } で { bm } = { 0, 0, ... } となります。
丸善出版の「パターン認識と機械学習」という書籍があります。以前、上巻だけを購入して読み進めていました。上巻は 6,500 円と高価でしたが、下巻はさらに高く 7,800 円もします。買うのはずっとためらっていたものの、上巻もだいぶ読み進めたので、本屋に立ち寄ったときに衝動買いしてしまいました。まだ上巻の残りを読んでいるところなので、もう少ししてから読もうと考えています。パターン認識関連の書籍はいろいろと買いましたが、高価なだけにこの本が一番まとまっている上に説明もある程度は細かく書かれていると思います。しかし、全部理解するにはあと 2, 3 冊、統計関係の書籍は必要になります。読むだけでもかなり苦労しました。
いい本だと思うので、図書館などにあれば借りて読むというのもオススメです。
2016 年名古屋大入試の理系最後の問題です。まだ、文系問題がふたつ残ってます。例によって合っている保証はありません。
-----
次の問に答えよ。ただし 2 次方程式の重解は 2 つと数える。
(1) 次の条件 (*) を満たす整数 a, b, c, d, e, f の組をすべて求めよ。
(*)
・2 次方程式 x2 + ax + b = 0 の 2 つの解が c, d である。
・2 次方程式 x2 + cx + d = 0 の 2 つの解が e, f である。
・2 次方程式 x2 + ex + f = 0 の 2 つの解が a, b である。
(2) 2 つの数列 { an }, { bn } は、次の条件 (**) を満たすものとする。
(**) すべての正の整数 n について、an, bn は整数であり、2 次方程式 x2 + anx + bn = 0 の 2 つの解が an+1, bn+1 である。
このとき、
(i) 正の整数 m で、| bm | = | bm+1 | = | bm+2 | = ... となるものが存在することを示せ。
(ii) 条件 (**) を満たす数列 { an }, { bn } の組をすべて求めよ。
(1) 二次方程式の解と係数の関係から
a = -c - d --- (a)
b = cd --- (b)
c = -e - f --- (c)
d = ef --- (d)
e = -a - b --- (e)
f = ab --- (f)
が成り立ちます。(b) を (f) に代入して f = acd、さらに (d) を代入すれば f = acef になります。
f ≠ 0 のとき、ace = 1 であり、これを満たす整数は a, c, e が全て 1 か、ひとつが 1 で残りが -1 の場合のみです。また、f ≠ 0 なので (b)(d) から b ≠ 0, d ≠ 0 となります。
(a) + (c) + (e) より
a + c + e = -( a + b + c + d + e + f )
2( a + c + e ) = -( b + d + f )
となるので、a = c = e = 1 なら b + d + f = -6 であり、(b)(d)(f) から b = d = f になります。
従って、この場合は { a, b, c, d, e, f } = { 1, -2, 1, -2, 1, -2 } です。
a = c = -1, e = 1 の場合、(a)(c)(e) より b = 0, d = 2, f = 0 となり、f ≠ 0 に反します。対称性から c = e = -1 かつ a = 1 の場合と e = a = -1 かつ c = 1 の場合も b, d, f のいずれかにゼロを含むため仮定に反します。
f = 0 のとき、(d) より d = 0, (b) より b = 0 となり、(a)(c)(e) より a = -c, c = -e, e = -a なので
a = -c = e = -a
となります。これを満たすのは a = 0 のときしかありません。対称性から同様に c = 0, e = 0 となるので、{ a, b, c, d, e, f } = { 0, 0, 0, 0, 0, 0 } となります。組はこの二つとなります。
(2)(i) 二次方程式の解と係数の関係から
am = -am+1 - bm+1 --- (a)
bm = am+1bm+1 --- (b)
が成り立つので、(b) より
bm = am+1bm+1 = am+1am+2bm+2 = ...
となります。任意の k > m に対して ak ≠ 0 ならば
bm / bm+1 = am+1
bm / bm+2 = am+1am+2
:
となるので、bm に対して bm+1 以降は全て約数とならなければなりません。また、
|am+1| ≤ |am+1am+2| ≤ ...
より
|bm / bm+1| ≤ |bm / bm+2| ≤ ...
なので
|bm+1| ≥ |bm+2| ≥ ...
となって、正の整数は有限なので必ずある値に収束します。最後に、am+1 = 0 となったとき、(b) より bm = 0 で、(b) の添字を一つ前にずらすと
bm-1 = ambm
なので bm-1 = 0 です。つまり、0 = b1 = b2= ... でありこの場合も成り立ちます。よて、命題が成り立つことが証明されました。
(2)(ii) (i) で証明した状態になったとき、(b) より bm ≠ 0 なら am はすべて ±1 となります。(a) にこの値を代入することで ( am, bm ) は ( bm ≠ 0 であることに注意して )
( am, bm ) = ( 1, -2 ), ( -1, 2 )
の二通りが得られます。( am, bm ) は解を ( am+1, bm+1 ) とする二次方程式の係数だったので、( 1, -2 ) のときは
x2 + x - 2 = 0
の解が ( am+1, bm+1 ) になります。その解は x = 1, -2 で、| am | = 1 という条件を満たすのは ( am+1, bm+1 ) = ( 1, -2 ) です。逆に、( am+1, bm+1 ) = ( 1, -2 ) なら (a)(b) より
am = -1 - ( -2 ) = 1
bm = 1・( -2 ) = -2
なので、全ての m に対して ( am, bm ) = ( 1, -2 ) ということになります。
( -1, 2 ) のときは
x2 - x + 2 = 0
の解が ( am+1, bm+1 ) になりますが、この方程式は整数解はおろか実数解もないので除外できます。
最後に、m がある値以上になったときに bm = 0 なら(a) より am = -am+1 なので、以降の am は絶対値の等しい値が符号だけ変化しながら続くことになります。その値を N としたとき、( am+1, bm+1 ) = ( N, 0 ) なら (a)(b) より
am = -N - 0 = -N
bm = N・0 = 0
であり、その前についても符号だけ変わって絶対値は変わりません。よって、任意の整数 N について { am } = { N, -N, N, ... } で { bm } = { 0, 0, ... } となります。
2016年03月16日
名大問題 2016 (3)
バンダイが「必殺技」を密かに登録商標にしようとしていたそうです。
意図がよくわかりませんが、いっそのこと「クソゲー」を登録商標にすればいいんじゃないでしょうか。もしくは「抱き合わせ」とか「課金制」とか。
必殺技といえば、似たような言葉に奥義とかありますよね。「北斗百裂拳」とか、あの言葉は登録商標されているんでしょうか。他にもドラえもんの道具の名前だとか、ちょっと気にはなりますね。
今年の名古屋大の問題から三つ目です。例によって合っている保証なしです。
-----
玉が 2 個ずつ入った 2 つの袋 A, B があるとき、袋 B から玉を 1 個取り出して袋 A に入れ、次に袋 A から玉を 1 個取り出して袋 B に入れる、という操作を 1 回の操作と数えることにする。
A に赤玉が 2 個、B に白玉が 2 個入った状態から始め、この操作を n 回繰り返した後に袋 B に入っている赤玉の個数が k 個である確率を Pn(k) ( n = 1, 2, 3, ... ) とする。
このとき、k = 0, 1, 2 に対する Pn(k) を求めよ (途中の導出問題は省略) (名古屋大 2016)。
一回の試行で起こる事象とその確率は、A( 赤, 赤 ) B( 白, 白 ) に対して
B から白を A へ → A から赤を B へ ... 2 / 3
B から白を A へ → A から白を B へ ... 1 / 3
なので、P1( 0 ) = 1 / 3, P1( 1 ) = 2 / 3, P1( 2 ) = 0 となります。n - 1 回の試行後の A, B の状態は
1. A( 赤, 赤 ) B( 白, 白 )
2. A( 赤, 白 ) B( 赤, 白 )
3. A( 白, 白 ) B( 赤, 赤 )
の 3 通りしかありません。この状態から試行を一回行ったときの事象とその確率は、1 の場合は先ほど求めたので 2, 3 について考えると
■ 2 の場合
B から赤を A へ ... 1 / 2 → A から赤を B へ ... 2 / 3 ( k = 1 )
B から赤を A へ ... 1 / 2 → A から白を B へ ... 1 / 3 ( k = 0 )
B から白を A へ ... 1 / 2 → A から赤を B へ ... 1 / 3 ( k = 2 )
B から白を A へ ... 1 / 2 → A から白を B へ ... 2 / 3 ( k = 1 )
■ 3 の場合
B から赤を A へ → A から赤を B へ ... 1 / 3 ( k = 2 )
B から赤を A へ → A から白を B へ ... 2 / 3 ( k = 1 )
1 の場合は k = 0 からのスタートなので、n - 1 回めの試行での確率は Pn-1( 0 ) です。同様に、2 の場合は Pn-1( 1 )、3 の場合は Pn-1( 2 ) となり、
Pn( 0 ) = ( 1 / 3 )Pn-1( 0 ) + ( 1 / 6 )Pn-1( 1 )
Pn( 1 ) = ( 2 / 3 )Pn-1( 0 ) + ( 2 / 3 )Pn-1( 1 ) + ( 2 / 3 )Pn-1( 2 )
Pn( 2 ) = ( 1 / 6 )Pn-1( 1 ) + ( 1 / 3 )Pn-1( 2 )
となります。Pn-1( 0 ) + Pn-1( 1 ) + Pn-1( 2 ) = 1 なので Pn-1( 2 ) = 1 - ( Pn-1( 0 ) + Pn-1( 1 ) ) を下側の 2 式に代入すると
Pn( 1 )
= ( 2 / 3 )Pn-1( 0 ) + ( 2 / 3 )Pn-1( 1 ) + ( 2 / 3 )[ 1 - ( Pn-1( 0 ) + Pn-1( 1 ) ) ]
= 2 / 3
Pn( 2 )
= ( 1 / 6 )Pn-1( 1 ) + ( 1 / 3 )[ 1 - ( Pn-1( 0 ) + Pn-1( 1 ) ) ]
= -( 1 / 3 )Pn-1( 0 ) - ( 1 / 6 )Pn-1( 1 ) + 1 / 3
となり、Pn( 1 ) は定数になります。従って、Pn-1( 1 ) = Pn( 1 ) = 2 / 3 であり、
Pn( 0 ) = ( 1 / 3 )Pn-1( 0 ) + 1 / 9
Pn( 2 ) = -( 1 / 3 )Pn-1( 0 ) + 2 / 9
という漸化式が得られます。
Pn( 0 ) - ( 1 / 3 )Pn-1( 0 ) = ( 1 / 3 )2
( 1 / 3 )Pn-1( 0 ) - ( 1 / 3 )2Pn-2( 0 ) = ( 1 / 3 )3
:
( 1 / 3 )n-2P2( 0 ) - ( 1 / 3 )n-1P1( 0 ) = ( 1 / 3 )n
を辺々加えて
Pn( 0 ) - ( 1 / 3 )n-1Pn-1( 0 ) = Σk{2→n}( ( 1 / 3 )k ) より
Pn( 0 ) = ( 1 / 6 ) - ( 3 / 2 )( 1 / 3 )n+1 + ( 1 / 3 )n
となります。また、Pn( 2 ) = 1 - Pn( 0 ) - Pn( 1 ) なので、
Pn( 2 ) = ( 1 / 6 ) + ( 3 / 2 )( 1 / 3 )n+1 - ( 1 / 3 )n
となります。
意図がよくわかりませんが、いっそのこと「クソゲー」を登録商標にすればいいんじゃないでしょうか。もしくは「抱き合わせ」とか「課金制」とか。
必殺技といえば、似たような言葉に奥義とかありますよね。「北斗百裂拳」とか、あの言葉は登録商標されているんでしょうか。他にもドラえもんの道具の名前だとか、ちょっと気にはなりますね。
今年の名古屋大の問題から三つ目です。例によって合っている保証なしです。
-----
玉が 2 個ずつ入った 2 つの袋 A, B があるとき、袋 B から玉を 1 個取り出して袋 A に入れ、次に袋 A から玉を 1 個取り出して袋 B に入れる、という操作を 1 回の操作と数えることにする。
A に赤玉が 2 個、B に白玉が 2 個入った状態から始め、この操作を n 回繰り返した後に袋 B に入っている赤玉の個数が k 個である確率を Pn(k) ( n = 1, 2, 3, ... ) とする。
このとき、k = 0, 1, 2 に対する Pn(k) を求めよ (途中の導出問題は省略) (名古屋大 2016)。
一回の試行で起こる事象とその確率は、A( 赤, 赤 ) B( 白, 白 ) に対して
B から白を A へ → A から赤を B へ ... 2 / 3
B から白を A へ → A から白を B へ ... 1 / 3
なので、P1( 0 ) = 1 / 3, P1( 1 ) = 2 / 3, P1( 2 ) = 0 となります。n - 1 回の試行後の A, B の状態は
1. A( 赤, 赤 ) B( 白, 白 )
2. A( 赤, 白 ) B( 赤, 白 )
3. A( 白, 白 ) B( 赤, 赤 )
の 3 通りしかありません。この状態から試行を一回行ったときの事象とその確率は、1 の場合は先ほど求めたので 2, 3 について考えると
■ 2 の場合
B から赤を A へ ... 1 / 2 → A から赤を B へ ... 2 / 3 ( k = 1 )
B から赤を A へ ... 1 / 2 → A から白を B へ ... 1 / 3 ( k = 0 )
B から白を A へ ... 1 / 2 → A から赤を B へ ... 1 / 3 ( k = 2 )
B から白を A へ ... 1 / 2 → A から白を B へ ... 2 / 3 ( k = 1 )
■ 3 の場合
B から赤を A へ → A から赤を B へ ... 1 / 3 ( k = 2 )
B から赤を A へ → A から白を B へ ... 2 / 3 ( k = 1 )
1 の場合は k = 0 からのスタートなので、n - 1 回めの試行での確率は Pn-1( 0 ) です。同様に、2 の場合は Pn-1( 1 )、3 の場合は Pn-1( 2 ) となり、
Pn( 0 ) = ( 1 / 3 )Pn-1( 0 ) + ( 1 / 6 )Pn-1( 1 )
Pn( 1 ) = ( 2 / 3 )Pn-1( 0 ) + ( 2 / 3 )Pn-1( 1 ) + ( 2 / 3 )Pn-1( 2 )
Pn( 2 ) = ( 1 / 6 )Pn-1( 1 ) + ( 1 / 3 )Pn-1( 2 )
となります。Pn-1( 0 ) + Pn-1( 1 ) + Pn-1( 2 ) = 1 なので Pn-1( 2 ) = 1 - ( Pn-1( 0 ) + Pn-1( 1 ) ) を下側の 2 式に代入すると
Pn( 1 )
= ( 2 / 3 )Pn-1( 0 ) + ( 2 / 3 )Pn-1( 1 ) + ( 2 / 3 )[ 1 - ( Pn-1( 0 ) + Pn-1( 1 ) ) ]
= 2 / 3
Pn( 2 )
= ( 1 / 6 )Pn-1( 1 ) + ( 1 / 3 )[ 1 - ( Pn-1( 0 ) + Pn-1( 1 ) ) ]
= -( 1 / 3 )Pn-1( 0 ) - ( 1 / 6 )Pn-1( 1 ) + 1 / 3
となり、Pn( 1 ) は定数になります。従って、Pn-1( 1 ) = Pn( 1 ) = 2 / 3 であり、
Pn( 0 ) = ( 1 / 3 )Pn-1( 0 ) + 1 / 9
Pn( 2 ) = -( 1 / 3 )Pn-1( 0 ) + 2 / 9
という漸化式が得られます。
Pn( 0 ) - ( 1 / 3 )Pn-1( 0 ) = ( 1 / 3 )2
( 1 / 3 )Pn-1( 0 ) - ( 1 / 3 )2Pn-2( 0 ) = ( 1 / 3 )3
:
( 1 / 3 )n-2P2( 0 ) - ( 1 / 3 )n-1P1( 0 ) = ( 1 / 3 )n
を辺々加えて
Pn( 0 ) - ( 1 / 3 )n-1Pn-1( 0 ) = Σk{2→n}( ( 1 / 3 )k ) より
Pn( 0 ) = ( 1 / 6 ) - ( 3 / 2 )( 1 / 3 )n+1 + ( 1 / 3 )n
となります。また、Pn( 2 ) = 1 - Pn( 0 ) - Pn( 1 ) なので、
Pn( 2 ) = ( 1 / 6 ) + ( 3 / 2 )( 1 / 3 )n+1 - ( 1 / 3 )n
となります。
2016年03月11日
名大問題 2016 (2)
震災から 5 年。今日はニュースでも特別枠が組まれ、復興の現状についてずっと放送されていました。
そして、それに埋もれるようにひっそりと、人工知能が囲碁界世界最強の棋士を二戦連勝で破るというニュースが流れ、さすがにゾッとしました。自分が思い浮かべる最悪の世界像は人工知能に支配されるというもの。しかし、人工知能が人間を超えてしまうのではなく、人間のほうが人工知能の利用で脳を退化させてしまうのが理由です。そうなると、もはや人工知能に頼らなければ生きてゆけなくなりますからね。
そうならないように、入試問題で脳のトレーニングをしました。合っている保証はありません。
-----
二つの円 C : ( x - 1 )2 + y2 = 1 と D : ( x + 2 )2 + y2 = 72 を考える。また原点を O( 0, 0 ) とする。このとき、次の問に答えよ。
円 C 上に、y 座標が正であるような点 P をとる。点 P が円 C 上を動き、点 Q が円 D 上を動くとき、ΔOPQ の面積の最大値を求めよ (途中の導出問題は省略) (名古屋大 2016)。
まず、x 軸の正の部分と線分 OP のなす角度を θ とします。点 P( px, py ) の座標を θ で表すと、
px = 1 - cos( π - 2θ ) = 1 + cos2θ
py = sin( π - 2θ ) = sin2θ
となります。また、OP の長さは 2cosθ となります。
点 P を固定したとき、ΔOPQが最大になるのは、OP を通る直線に円 D の中心 ( -2, 0 ) からひいた垂線が円 D と交差する点を Q としたときになります。これは、( -2, 0 ) を通り、ベクトル OP = ( 1 + cos2θ, sin2θ ) と直交する直線との交点を意味するので、まずはこの直線の方程式を求めると、
1 + cos2θ = 2cos2θ
sin2θ = 2sinθcosθ
より、求める直線の方向ベクトルを ( 1, t ) とすると
2cos2θ + 2tsinθcosθ = 0
を満たせばよく、0 < θ < π / 2 より cosθ ≠ 0 なので
t = -cosθ / sinθ = -1 / tanθ
となります。従って、直線の方程式は
y = ( -1 / tanθ )( x +2 )
となって、円 D との交点は
( x + 2 )2 + ( x + 2 )2 / tan2θ = 72
を計算することによって
( x, y ) = ( 7sinθ - 2, -7cosθ ), ( -7sinθ - 2, 7cosθ )
となります。
直線 OP は y = x tanθ なので、先ほど求めた垂線 y = ( -1 / tanθ )( x +2 ) との交点は
( x, y ) = ( -2cos2θ, -2sinθcosθ )
となります。従って、ΔOPQ の高さは、( x, y ) = ( 7sinθ - 2, -7cosθ ) のとき
( -2cos2θ - 7sinθ + 2 )2 + ( -2sinθcosθ + 7cosθ )2
= ( 2sinθ - 7 )2sin2θ + ( 2sinθ - 7 )2cos2θ
= ( 2sinθ - 7 )2
より ( 0 < sinθ < 1 なので ) 7 - 2sinθ であり、( -7sinθ - 2, 7cosθ ) の場合も同様に計算して 7 + 2sinθ となります。よって ΔOPQ の面積は
( 7 ± 2sinθ )cosθ = 7cosθ ± sin2θ
となり、0 < θ < π / 2 より sin2θ > 0 なので最大をとるのは 7cosθ + sin2θ の方です。これを θ に対して微分すると
f'(θ)
= -7sinθ + 2cos2θ
= -7sinθ + 2( 1 - 2sin2θ )
= -4sin2θ - 7sinθ + 2
なので、f'(θ) = 0 のとき
sinθ = [ -7 ± ( 72 + 4・4・2 )1/2 ] / ( 2・4 ) = -2, 1 / 4
となって、0 < sinθ < 1 より 1 / 4 が解となります。このとき cosθ = √15 / 4 なので、
7cosθ + sin2θ = 7cosθ + 2sinθcosθ ≤ 7√15 / 4 + 2・( 1 / 4 )・( √15 / 4 ) = 15√15 / 8 となります。
そして、それに埋もれるようにひっそりと、人工知能が囲碁界世界最強の棋士を二戦連勝で破るというニュースが流れ、さすがにゾッとしました。自分が思い浮かべる最悪の世界像は人工知能に支配されるというもの。しかし、人工知能が人間を超えてしまうのではなく、人間のほうが人工知能の利用で脳を退化させてしまうのが理由です。そうなると、もはや人工知能に頼らなければ生きてゆけなくなりますからね。
そうならないように、入試問題で脳のトレーニングをしました。合っている保証はありません。
-----
二つの円 C : ( x - 1 )2 + y2 = 1 と D : ( x + 2 )2 + y2 = 72 を考える。また原点を O( 0, 0 ) とする。このとき、次の問に答えよ。
円 C 上に、y 座標が正であるような点 P をとる。点 P が円 C 上を動き、点 Q が円 D 上を動くとき、ΔOPQ の面積の最大値を求めよ (途中の導出問題は省略) (名古屋大 2016)。
まず、x 軸の正の部分と線分 OP のなす角度を θ とします。点 P( px, py ) の座標を θ で表すと、
px = 1 - cos( π - 2θ ) = 1 + cos2θ
py = sin( π - 2θ ) = sin2θ
となります。また、OP の長さは 2cosθ となります。
点 P を固定したとき、ΔOPQが最大になるのは、OP を通る直線に円 D の中心 ( -2, 0 ) からひいた垂線が円 D と交差する点を Q としたときになります。これは、( -2, 0 ) を通り、ベクトル OP = ( 1 + cos2θ, sin2θ ) と直交する直線との交点を意味するので、まずはこの直線の方程式を求めると、
1 + cos2θ = 2cos2θ
sin2θ = 2sinθcosθ
より、求める直線の方向ベクトルを ( 1, t ) とすると
2cos2θ + 2tsinθcosθ = 0
を満たせばよく、0 < θ < π / 2 より cosθ ≠ 0 なので
t = -cosθ / sinθ = -1 / tanθ
となります。従って、直線の方程式は
y = ( -1 / tanθ )( x +2 )
となって、円 D との交点は
( x + 2 )2 + ( x + 2 )2 / tan2θ = 72
を計算することによって
( x, y ) = ( 7sinθ - 2, -7cosθ ), ( -7sinθ - 2, 7cosθ )
となります。
直線 OP は y = x tanθ なので、先ほど求めた垂線 y = ( -1 / tanθ )( x +2 ) との交点は
( x, y ) = ( -2cos2θ, -2sinθcosθ )
となります。従って、ΔOPQ の高さは、( x, y ) = ( 7sinθ - 2, -7cosθ ) のとき
( -2cos2θ - 7sinθ + 2 )2 + ( -2sinθcosθ + 7cosθ )2
= ( 2sinθ - 7 )2sin2θ + ( 2sinθ - 7 )2cos2θ
= ( 2sinθ - 7 )2
より ( 0 < sinθ < 1 なので ) 7 - 2sinθ であり、( -7sinθ - 2, 7cosθ ) の場合も同様に計算して 7 + 2sinθ となります。よって ΔOPQ の面積は
( 7 ± 2sinθ )cosθ = 7cosθ ± sin2θ
となり、0 < θ < π / 2 より sin2θ > 0 なので最大をとるのは 7cosθ + sin2θ の方です。これを θ に対して微分すると
f'(θ)
= -7sinθ + 2cos2θ
= -7sinθ + 2( 1 - 2sin2θ )
= -4sin2θ - 7sinθ + 2
なので、f'(θ) = 0 のとき
sinθ = [ -7 ± ( 72 + 4・4・2 )1/2 ] / ( 2・4 ) = -2, 1 / 4
となって、0 < sinθ < 1 より 1 / 4 が解となります。このとき cosθ = √15 / 4 なので、
7cosθ + sin2θ = 7cosθ + 2sinθcosθ ≤ 7√15 / 4 + 2・( 1 / 4 )・( √15 / 4 ) = 15√15 / 8 となります。
2016年03月10日
名大問題 2016 (1)
暖かくなったと思ったら寒くなったり。はっきりしない季節ですね。
「保育園落ちた」のブログが国会でも取り上げられたのがニュースになっていました。野党が利用しただけとかいろいろ言われてはいますが、ネットでのつぶやきが国会にまで影響を及ぼすというのは驚きです。前にも同じようなことってありましたっけ?今までは議員本人のつぶやきが取り上げられることしかなかったように記憶してます。
一応、前向きに検討しているみたいですけど、つぶやいた本人はすぐにでもなんとかしてほしいんじゃないでしょうか。
さて、今年の名古屋大の入試問題を一通り解いてみました。合っている保証なしですが、その中の一つを公開しておきます。
-----
曲線 y = x2 上に 2 点 A ( -2, 4 ), B ( b, b2 ) をとる。ただし b > -2 とする。このとき、次の条件を満たす b の範囲を求めよ (名古屋大 2016)。
条件 : y = x2 上の点 T ( t, t2 ) で、∠ATB が直角になるものが存在する。
A を任意の点 ( a, a2 ) として解いてみます。まず、ベクトル TA と BT を求めると、
TA = ( t - a, t2 - a2 )
BT = ( b - t, b2 - t2 )
となります。∠ATB が直角ということは、この二つのベクトルが直交するということなので、内積 ( TA, BT ) = 0 となる点 T が a < t < b に存在すればいいことになります。この内積は
( t - a )( b - t ) + ( t2 - a2 )( b2 - t2 ) = ( t - a )( b - t )[ 1 + ( t + a )( b + t ) ]
となりますが、t - a > 0, b - t > 0 なので、
f(t) = 1 + ( t + a )( b + t ) = t2 + ( a + b )t + ( ab + 1 )
に対し、f(t) = 0 が a < t < b の範囲で解を持つことが必要になります。判別式 D は
D = ( a + b )2 - 4( ab + 1 ) = ( a - b )2 - 4
より、f(t) = 0 が実数解を持つためには ( a - b )2 ≥ 4 が成り立たなければなりません。まず、これがひとつ目の条件になります。
f(t) = 0 の解は { -( a + b ) ± [ ( a - b )2 - 4 ]1/2 } / 2 となることから、
2a < -( a + b ) + [ ( a - b )2 - 4 ]1/2 --- (1)
-( a + b ) - [ ( a - b )2 - 4 ]1/2 < 2b --- (2)
のいずれかとなれば、解は区間 ( a, b ) の間に入ります。(1) より
3a + b < [ ( a - b )2 - 4 ]1/2
( 3a + b )2 = 9a2 + 6ab + b2 < a2 - 2ab + b2 - 4
8ab + 8a2 + 4 < 0 を解いて
a < 0 のとき b > -( 2a2 + 1 ) / 2a
a > 0 のとき b < -( 2a2 + 1 ) / 2a
となります。また (2) より
[ ( a - b )2 - 4 ]1/2 > -a - 3b
( a - b )2 - 4 = a2 - 2ab + b2 - 4 > ( -a - 3b )2 = a2 + 6ab + 9b2
2b2 + 2ab + 1 < 0
b を変数とする (左辺) = 0 の解は [ -a ± ( a2 - 2 )1/2 ] / 2 なので、
[ -a - ( a2 - 2 )1/2 ] / 2 < b < [ -a + ( a2 - 2 )1/2 ] / 2
が求める範囲になります。これがふたつ目の条件です。
問いでは a = -2 なので、ひとつ目の条件から
( -2 - b )2 ≥ 4 より b( b + 4 ) ≥ 0
が成り立てばよく、b > -2 から b + 4 > 0 なので、b ≥ 0 であればいいことになります。ふたつ目の条件から
b > 9 / 4
( 2 - √2 ) / 2 < b < ( 2 + √2 ) / 2
となって、全てを合わせれば
( 2 - √2 ) / 2 < b < ( 2 + √2 ) / 2 または b > 9 / 4
となります。文系では a = -1 だったようです。このときはひとつ目の条件から
( -1 - b )2 ≥ 4 より ( b + 3 )( b - 1 ) ≥ 0 なので b < -3, 1 < b であり、ふたつ目の条件から
b > 3 / 2
( 1 - i ) / 2 < b < ( 1 + i ) / 2 [虚数解なので対象なし]
なので、b > 3 / 2 が求める解となります。
「保育園落ちた」のブログが国会でも取り上げられたのがニュースになっていました。野党が利用しただけとかいろいろ言われてはいますが、ネットでのつぶやきが国会にまで影響を及ぼすというのは驚きです。前にも同じようなことってありましたっけ?今までは議員本人のつぶやきが取り上げられることしかなかったように記憶してます。
一応、前向きに検討しているみたいですけど、つぶやいた本人はすぐにでもなんとかしてほしいんじゃないでしょうか。
さて、今年の名古屋大の入試問題を一通り解いてみました。合っている保証なしですが、その中の一つを公開しておきます。
-----
曲線 y = x2 上に 2 点 A ( -2, 4 ), B ( b, b2 ) をとる。ただし b > -2 とする。このとき、次の条件を満たす b の範囲を求めよ (名古屋大 2016)。
条件 : y = x2 上の点 T ( t, t2 ) で、∠ATB が直角になるものが存在する。
A を任意の点 ( a, a2 ) として解いてみます。まず、ベクトル TA と BT を求めると、
TA = ( t - a, t2 - a2 )
BT = ( b - t, b2 - t2 )
となります。∠ATB が直角ということは、この二つのベクトルが直交するということなので、内積 ( TA, BT ) = 0 となる点 T が a < t < b に存在すればいいことになります。この内積は
( t - a )( b - t ) + ( t2 - a2 )( b2 - t2 ) = ( t - a )( b - t )[ 1 + ( t + a )( b + t ) ]
となりますが、t - a > 0, b - t > 0 なので、
f(t) = 1 + ( t + a )( b + t ) = t2 + ( a + b )t + ( ab + 1 )
に対し、f(t) = 0 が a < t < b の範囲で解を持つことが必要になります。判別式 D は
D = ( a + b )2 - 4( ab + 1 ) = ( a - b )2 - 4
より、f(t) = 0 が実数解を持つためには ( a - b )2 ≥ 4 が成り立たなければなりません。まず、これがひとつ目の条件になります。
f(t) = 0 の解は { -( a + b ) ± [ ( a - b )2 - 4 ]1/2 } / 2 となることから、
2a < -( a + b ) + [ ( a - b )2 - 4 ]1/2 --- (1)
-( a + b ) - [ ( a - b )2 - 4 ]1/2 < 2b --- (2)
のいずれかとなれば、解は区間 ( a, b ) の間に入ります。(1) より
3a + b < [ ( a - b )2 - 4 ]1/2
( 3a + b )2 = 9a2 + 6ab + b2 < a2 - 2ab + b2 - 4
8ab + 8a2 + 4 < 0 を解いて
a < 0 のとき b > -( 2a2 + 1 ) / 2a
a > 0 のとき b < -( 2a2 + 1 ) / 2a
となります。また (2) より
[ ( a - b )2 - 4 ]1/2 > -a - 3b
( a - b )2 - 4 = a2 - 2ab + b2 - 4 > ( -a - 3b )2 = a2 + 6ab + 9b2
2b2 + 2ab + 1 < 0
b を変数とする (左辺) = 0 の解は [ -a ± ( a2 - 2 )1/2 ] / 2 なので、
[ -a - ( a2 - 2 )1/2 ] / 2 < b < [ -a + ( a2 - 2 )1/2 ] / 2
が求める範囲になります。これがふたつ目の条件です。
問いでは a = -2 なので、ひとつ目の条件から
( -2 - b )2 ≥ 4 より b( b + 4 ) ≥ 0
が成り立てばよく、b > -2 から b + 4 > 0 なので、b ≥ 0 であればいいことになります。ふたつ目の条件から
b > 9 / 4
( 2 - √2 ) / 2 < b < ( 2 + √2 ) / 2
となって、全てを合わせれば
( 2 - √2 ) / 2 < b < ( 2 + √2 ) / 2 または b > 9 / 4
となります。文系では a = -1 だったようです。このときはひとつ目の条件から
( -1 - b )2 ≥ 4 より ( b + 3 )( b - 1 ) ≥ 0 なので b < -3, 1 < b であり、ふたつ目の条件から
b > 3 / 2
( 1 - i ) / 2 < b < ( 1 + i ) / 2 [虚数解なので対象なし]
なので、b > 3 / 2 が求める解となります。
2016年02月07日
暦の上では春
立春が過ぎました。暦の上では春ですね。
この間の寒波からまた一転して、朝でも強烈な寒さというのは少なくなったような気がします。それでもやはり寒いですけど。
久々に数学問題にチャレンジしました。かなり前に「数学問題bot」で拾った問題です。毎度のように、合っている保証なしです。
-----
n 枚の 100 円玉と n + 1 枚の 500 円玉を同時に投げたとき、表の出た 100 円玉の枚数より表の出た 500 円玉の枚数の方が多い確率を求めよ ( 05 京都 )
まず、すべての場合の数は 22n+1 になります。n 枚の 100 円玉がすべて表だったとき、500 円玉の方が表の出た数が多くなるのは n + 1 枚全てが表だった時に限るので、それは n+1Cn+1 = 1 通りのみとなります。1 枚減って n - 1 枚の 100 円玉が表なら、n 枚か n + 1 枚の 500 円玉が表なら成り立つので、n 枚の 500 円玉が表の場合の数を考えるとそれは n+1Cn = n + 1 通りで、n + 1 枚の 500 円玉が表の場合と併せて n + 2 通りになります。このように順番に考えると、k 枚の 100 円玉が表なら、k - 1 枚が表だったときの結果に n+1Ck 通りを加算した場合の数だけ成り立つことがわかります。これを図に書いてみると
となります。500 円玉のみでの全ての場合の数は 2n+1 となります。さらに、上の表をよく見ると、値のある部分とゼロの部分でちょうど半分ずつになっていることがわかります。このとき、NCK = NCN-K なので、例えば、0 枚、n 枚の 100 円玉が表の場合に成り立つ場合の数を足すとちょうど 2n+1 に等しくなります。また、0 枚、n 枚の 100 円玉が表になる場合の数はどちらも 1 通りなので、このときの場合の数は合計で 2n+1 です。同様の考え方から、1 枚、n - 1 枚の 100 円玉が表になるときは合計が 2n+1 x n、もっと一般的に、k 枚、n - k 枚の 100 円玉が表になるときは合計が 2n+1 x nCk です。つまり、求めたい場合の数の総計は、
Σk{0→n}( 2n+1 x nCk ) / 2 = 2nΣk{0→n}( nCk ) = 22n
です。よって、求める確率は
22n / 22n+1 = 1 / 2
になります。n = 2 の場合で検算してみると、100 円玉を a, b、500 円玉を C, D, E で表して、すべての場合を調べれば
となって、ちゃんと 1/2 になります。
ところで、さらりと
Σk{0→n}( 2n+1 x nCk ) / 2 = 2nΣk{0→n}( nCk ) = 22n
と書きましたが、これは
Σk{0→n}( nCk ) = 2n
であることを利用しています。この式の一般化は
Σk{0→n}( nCkakbn-k ) = ( a + b )n
で「二項定理」と呼ばれています。「パスカルの三角形」としても有名ですね。二項式の係数が組み合わせの値で表せるので、組み合わせは二項係数ともいいます。この定理、いつどこで習ったのか、そもそも学校で習ったのか全く記憶がないのですが、結構重要な定理なので、ぜひとも覚えておいたほうがいいですよ。特に受験生の方は。ちなみに自分が高校生の頃、この定理を知っていたかどうか定かではないんですよね。
それから、この問題はもしかしたら帰納法でも解けるかもしれません。暇な時に試してみようかと思います。
この間の寒波からまた一転して、朝でも強烈な寒さというのは少なくなったような気がします。それでもやはり寒いですけど。
久々に数学問題にチャレンジしました。かなり前に「数学問題bot」で拾った問題です。毎度のように、合っている保証なしです。
-----
n 枚の 100 円玉と n + 1 枚の 500 円玉を同時に投げたとき、表の出た 100 円玉の枚数より表の出た 500 円玉の枚数の方が多い確率を求めよ ( 05 京都 )
まず、すべての場合の数は 22n+1 になります。n 枚の 100 円玉がすべて表だったとき、500 円玉の方が表の出た数が多くなるのは n + 1 枚全てが表だった時に限るので、それは n+1Cn+1 = 1 通りのみとなります。1 枚減って n - 1 枚の 100 円玉が表なら、n 枚か n + 1 枚の 500 円玉が表なら成り立つので、n 枚の 500 円玉が表の場合の数を考えるとそれは n+1Cn = n + 1 通りで、n + 1 枚の 500 円玉が表の場合と併せて n + 2 通りになります。このように順番に考えると、k 枚の 100 円玉が表なら、k - 1 枚が表だったときの結果に n+1Ck 通りを加算した場合の数だけ成り立つことがわかります。これを図に書いてみると
| 500円玉 | |||||||
| 100円玉 | n+1 | n | n-1 | ... | 2 | 1 | 0 |
| n | n+1Cn+1 | 0 | 0 | ... | 0 | 0 | 0 |
| n-1 | n+1Cn+1 | n+1Cn | 0 | ... | 0 | 0 | 0 |
| n-2 | n+1Cn+1 | n+1Cn | n+1Cn-1 | ... | 0 | 0 | 0 |
| : | |||||||
| 1 | n+1Cn+1 | n+1Cn | n+1Cn-1 | ... | n+1C2 | 0 | 0 |
| 0 | n+1Cn+1 | n+1Cn | n+1Cn-1 | ... | n+1C2 | n+1C1 | 0 |
となります。500 円玉のみでの全ての場合の数は 2n+1 となります。さらに、上の表をよく見ると、値のある部分とゼロの部分でちょうど半分ずつになっていることがわかります。このとき、NCK = NCN-K なので、例えば、0 枚、n 枚の 100 円玉が表の場合に成り立つ場合の数を足すとちょうど 2n+1 に等しくなります。また、0 枚、n 枚の 100 円玉が表になる場合の数はどちらも 1 通りなので、このときの場合の数は合計で 2n+1 です。同様の考え方から、1 枚、n - 1 枚の 100 円玉が表になるときは合計が 2n+1 x n、もっと一般的に、k 枚、n - k 枚の 100 円玉が表になるときは合計が 2n+1 x nCk です。つまり、求めたい場合の数の総計は、
Σk{0→n}( 2n+1 x nCk ) / 2 = 2nΣk{0→n}( nCk ) = 22n
です。よって、求める確率は
22n / 22n+1 = 1 / 2
になります。n = 2 の場合で検算してみると、100 円玉を a, b、500 円玉を C, D, E で表して、すべての場合を調べれば
| a | b | C | D | E | 結果 |
|---|---|---|---|---|---|
| × | |||||
| 表 | ○ | ||||
| 表 | ○ | ||||
| 表 | ○ | ||||
| 表 | 表 | ○ | |||
| 表 | 表 | ○ | |||
| 表 | 表 | ○ | |||
| 表 | 表 | 表 | ○ | ||
| 表 | × | ||||
| 表 | 表 | × | |||
| 表 | 表 | × | |||
| 表 | 表 | × | |||
| 表 | 表 | 表 | ○ | ||
| 表 | 表 | 表 | ○ | ||
| 表 | 表 | 表 | ○ | ||
| 表 | 表 | 表 | 表 | ○ | |
| 表 | × | ||||
| 表 | 表 | × | |||
| 表 | 表 | × | |||
| 表 | 表 | × | |||
| 表 | 表 | 表 | ○ | ||
| 表 | 表 | 表 | ○ | ||
| 表 | 表 | 表 | ○ | ||
| 表 | 表 | 表 | 表 | ○ | |
| 表 | 表 | × | |||
| 表 | 表 | 表 | × | ||
| 表 | 表 | 表 | × | ||
| 表 | 表 | 表 | × | ||
| 表 | 表 | 表 | 表 | × | |
| 表 | 表 | 表 | 表 | × | |
| 表 | 表 | 表 | 表 | × | |
| 表 | 表 | 表 | 表 | 表 | ○ |
となって、ちゃんと 1/2 になります。
ところで、さらりと
Σk{0→n}( 2n+1 x nCk ) / 2 = 2nΣk{0→n}( nCk ) = 22n
と書きましたが、これは
Σk{0→n}( nCk ) = 2n
であることを利用しています。この式の一般化は
Σk{0→n}( nCkakbn-k ) = ( a + b )n
で「二項定理」と呼ばれています。「パスカルの三角形」としても有名ですね。二項式の係数が組み合わせの値で表せるので、組み合わせは二項係数ともいいます。この定理、いつどこで習ったのか、そもそも学校で習ったのか全く記憶がないのですが、結構重要な定理なので、ぜひとも覚えておいたほうがいいですよ。特に受験生の方は。ちなみに自分が高校生の頃、この定理を知っていたかどうか定かではないんですよね。
それから、この問題はもしかしたら帰納法でも解けるかもしれません。暇な時に試してみようかと思います。
2015年10月15日
脱ヌード
Playboy Magazine が、ヌードの掲載をやめるという記事が新聞に載っていました。Live Science でもこの話題を取り上げて、"Bye, Bye, Playboy, Bunnies" という記事を掲載していました。副題が「ポルノが脳に与える五つの影響」ということで、果たしてポルノは脳にいい影響を与えるのかどうか、全く正反対な二つの作用について書かれています。
今ではインターネットの普及で Web 上でも簡単にヌード画像が閲覧できてしまうので、ヌード写真を掲載した雑誌というものも淘汰されてきているようです。プレイボーイも同様で、売り上げは下降状態。で、ヌードの掲載を一時的にやめたら逆に売り上げが伸びたそうです。年齢層も下がったということで、ヌードがなくなって買いやすくなったんでしょうか。いやいや、中学生じゃあるまいし。
「数学問題bot」から、なかなか面白い問題です。
-----
n! が n^2 の倍数となるような自然数 n を全て求めよ ( 11 東工大 AO )
n! = Kn2 より、両辺を n で割って
( n - 1 )! = Kn となるような自然数 K が存在すればいいので、( n - 1 )! が n で割り切れるような自然数をすべて求めればよいことになります。n = 1 ならば明らかに成り立ち、n = 2 は成り立たないことは簡単に示すことができます。n = 3 の場合、( n - 1 )! = 2 は 3 で割り切れないので成り立ちません。n = 4 では ( n - 1 )! = 6 となり、これもNGです。以下、計算すると
となります。まず、素数に対しては成り立たないようにみえるのでこれを証明すると、p を素数とした時、1 から p - 1 までのすべての数は p と互いに素です。従って、( p - 1 )! には p と共通な因数は存在せず、従って成り立たないことがわかります。しかし、p2 ならば、1 から p2 までの間の p の倍数は p, 2p, ... p2 の p 個あるので、( p2 - 1 )! には p が p - 1 個含まれることになり、p - 1 ≥ 2 ならば、( p2 - 1 )! は p2 で割り切れます。従って、p ≥ 3 ならば、p2 は成り立つことになります。
さらに一般化して pm ( m ≥ 2 ) の場合を考えると、1 から pm までの間の p の倍数は p, 2p, ... pm-1・p の pm-1 個あり、k ≤ m の任意の k について、pk の倍数は pk, 2pk, ... pm-kpk の pm-k 個あります。pk の倍数には k 個の p があり、k より小さな指数の倍数でもあることから、k = 1 の場合から順に p をひとつずつ抽出したと考えれば、p の総数は
pm-1 + pm-2 + ... + p + 1 = pm - 1 個
になります。しかし、これは pm! にある p の総数なので、実際にはここから m を引いた個数が ( pm - 1 )! に含まれる p の個数です。従って
pm - m - 1 ≥ m より
pm ≥ 2m + 1
ならば pm は成り立つことになります。この不等式は、( p, m ) = ( 2, 2 ) 以外の全ての数 ( 但し m ≥ 2 です ) で成り立ちます。
最後に、n を二つ以上の異なる素因数からなる任意の合成数としたとき、その中の一つの素因数を p として n は
n = Kpm
という形で表すことができます。但し、K ≥ 2, m ≥ 1 とします。( n - 1 )! には pm の倍数が K - 1 個あるので、K ≥ 2 ならば必ず pm で割り切れることになります。どの素因数に対してもこれは成り立つので、二つ以上の異なる素因数を持つ合成数は全て成り立つことになります。
従って、求める自然数は、
1
22 を除いた素数のべき乗数全て
二つ以上の異なる素因数からなる合成数
になります。
例によって、合ってるかどうかは不明です。
今ではインターネットの普及で Web 上でも簡単にヌード画像が閲覧できてしまうので、ヌード写真を掲載した雑誌というものも淘汰されてきているようです。プレイボーイも同様で、売り上げは下降状態。で、ヌードの掲載を一時的にやめたら逆に売り上げが伸びたそうです。年齢層も下がったということで、ヌードがなくなって買いやすくなったんでしょうか。いやいや、中学生じゃあるまいし。
「数学問題bot」から、なかなか面白い問題です。
-----
n! が n^2 の倍数となるような自然数 n を全て求めよ ( 11 東工大 AO )
n! = Kn2 より、両辺を n で割って
( n - 1 )! = Kn となるような自然数 K が存在すればいいので、( n - 1 )! が n で割り切れるような自然数をすべて求めればよいことになります。n = 1 ならば明らかに成り立ち、n = 2 は成り立たないことは簡単に示すことができます。n = 3 の場合、( n - 1 )! = 2 は 3 で割り切れないので成り立ちません。n = 4 では ( n - 1 )! = 6 となり、これもNGです。以下、計算すると
| n | ( n - 1 )! | 割り切れるか? |
| 5 | 24 | × |
| 6 | 120 | ○ |
| 7 | 720 | × |
| 8 | 5040 | ○ |
| 9 | 40320 | ○ |
| 10 | 362880 | ○ |
となります。まず、素数に対しては成り立たないようにみえるのでこれを証明すると、p を素数とした時、1 から p - 1 までのすべての数は p と互いに素です。従って、( p - 1 )! には p と共通な因数は存在せず、従って成り立たないことがわかります。しかし、p2 ならば、1 から p2 までの間の p の倍数は p, 2p, ... p2 の p 個あるので、( p2 - 1 )! には p が p - 1 個含まれることになり、p - 1 ≥ 2 ならば、( p2 - 1 )! は p2 で割り切れます。従って、p ≥ 3 ならば、p2 は成り立つことになります。
さらに一般化して pm ( m ≥ 2 ) の場合を考えると、1 から pm までの間の p の倍数は p, 2p, ... pm-1・p の pm-1 個あり、k ≤ m の任意の k について、pk の倍数は pk, 2pk, ... pm-kpk の pm-k 個あります。pk の倍数には k 個の p があり、k より小さな指数の倍数でもあることから、k = 1 の場合から順に p をひとつずつ抽出したと考えれば、p の総数は
pm-1 + pm-2 + ... + p + 1 = pm - 1 個
になります。しかし、これは pm! にある p の総数なので、実際にはここから m を引いた個数が ( pm - 1 )! に含まれる p の個数です。従って
pm - m - 1 ≥ m より
pm ≥ 2m + 1
ならば pm は成り立つことになります。この不等式は、( p, m ) = ( 2, 2 ) 以外の全ての数 ( 但し m ≥ 2 です ) で成り立ちます。
最後に、n を二つ以上の異なる素因数からなる任意の合成数としたとき、その中の一つの素因数を p として n は
n = Kpm
という形で表すことができます。但し、K ≥ 2, m ≥ 1 とします。( n - 1 )! には pm の倍数が K - 1 個あるので、K ≥ 2 ならば必ず pm で割り切れることになります。どの素因数に対してもこれは成り立つので、二つ以上の異なる素因数を持つ合成数は全て成り立つことになります。
従って、求める自然数は、
1
22 を除いた素数のべき乗数全て
二つ以上の異なる素因数からなる合成数
になります。
例によって、合ってるかどうかは不明です。
2015年10月07日
新しい窓達
仕事で Windows2012 の再インストール作業をすることになりました。初めて使った時は、あまりにも操作方法が変わってしまって設定にかなり手こずってましたが、最近はだいぶ慣れてきたような気が。しかし、リモートデスクトップサービスを使うのにドメインを立ちあげなければならなくなったりして結構面倒です。そういえば、次のバージョンはいつ頃出るんでしたっけね。クライアント用には Windows10 が発表されて間もないわけですが、今のところ使う気にはならないです。しかし、また PC を買い換える頃にはこれしかないような状態になりそうです。
今回は、「マテマティカ2」からの問題を解いてみました。ちょっと前からいろいろと解き方を考えていましたが、ようやく解法が見つかりました (正解しているかはわかりませんが)。
-----
153: 複素数
p を素数、a, b を互いに素である自然数とする。( a + bi )^p が実数をとるような a, b, p の組み合わせは何組あるか。ただし、i は虚数単位とする。
二項定理より
( a + bi )p = ap + pC1ap-1・bi + ... + pCkap-k・(bi)k + ... + pCp(bi)p
なので、虚部は bi の指数が奇数の部分で表されます。p = 2 のときは
( a + bi )2 = ( a2 - b2 ) + 2abi
なので、これが実数となるためには ab = 0 である必要がありこれは成り立ちません。従って、p は奇素数の場合だけを考えればよいことになります。任意の奇素数に対し、その虚部は
[ pC1ap-1・b - pC3ap-3・b3 + ... + (-1)(k-1)/2pCkap-k・bk + ... + (-1)(p-1)/2pCpbp ]i
= i・Σk{1→(p+1)/2}( (-1)k-1pC2k-1ap-2k+1・b2k-1 )
となります。従って、これがゼロになれば、( a + bi )p は実数となります。虚数 i を除いて係数部分だけとし、b ≠ 0 より、b で割ると
pC1ap-1 - pC3ap-3・b2 + ... + (-1)(k-1)/2pCkap-k・bk-1 + ... + (-1)(p-1)/2pCpbp-1
= pC1ap-1 - pC3ap-3・b2 + ... + (-1)(k-1)/2pCkap-k・bk-1 + ... + (-1)(p-1)/2bp-1
= 0
より
pC1ap-1 - pC3ap-3・b2 + ... + (-1)(k-1)/2pCkap-k・bk-1 + ... + (-1)(p-3)/2pCp-2a2・bp-3 = -(-1)(p-1)/2bp-1
となりますが、p > k > 0 ならば pCk は必ず p の倍数となるので(証明は後述)、左辺は p の倍数となり、従って右辺にある b は p を素因数に持つ必要があります (左辺がゼロの場合 b = 0 となるのでこの場合は無視できます)。そこで今度は b = pc とすると、
pC1ap-1 - pC3ap-3・(pc)2 + ... + (-1)(k-1)/2pCkap-k・(pc)k-1 + ... + (-1)(p-1)/2(pc)p-1
= pC1ap-1 - p2pC3ap-3・c2 + ... + (-1)(k-1)/2pk-1pCkap-k・ck-1 + ...
+ (-1)(p-1)/2pp-1cp-1
= 0
より
-p2pC3ap-3・c2 + ... + (-1)(k-1)/2pk-1pCkap-k・ck-1 + ... + (-1)(p-1)/2pp-1cp-1 = -pC1ap-1
となり、両辺を p で割れば
-ppC3ap-3・c2 + ... + (-1)(k-1)/2pk-2pCkap-k・ck-1 + ... + (-1)(p-1)/2pp-2cp-1 = -ap-1
なので a も p を素因数として持つことになり、a, b が互いに素であるという仮定に反します。従って、( a + bi )p が実数となるような ( a, b, p ) の組み合わせは存在しないということになります。
p > k > 0 ならば pCk は必ず p の倍数となることの証明ですが、
pCk = p! / k!・( p - k )! = p・( p - 1 )・...・( p - k + 1 ) / k・( k - 1 )・...・2・1
より p が素数で p > k ならば、分母の 1 から k までの数で p を割ることはできないので、pCk が整数なら p はそのまま素因数として残ることになり、従って pCk は p の倍数となります。pCk が整数であることの証明は(組み合わせを表すので当然ではありますが)、
p-1Ck + p-1Ck-1
= ( p - 1 )! / k!・( p - k - 1 )! + ( p - 1 )! / ( k - 1 )!・( p - k )!
= [ ( p - 1 )! / ( k - 1 )!・( p - k - 1 )! ][ 1 / k + 1 / ( p - k ) ]
= [ ( p - 1 )! / ( k - 1 )!・( p - k - 1 )! ]{ [ ( p - k ) + k ] / k( p - k ) ]
= [ ( p - 1 )! / ( k - 1 )!・( p - k - 1 )! ][ p / k( p - k ) ]
= p! / k!・( p - k )! = pCk
より、pCk は p-1Ck + p-1Ck-1 の和で表すことができます。従って、p-1Ck が任意の k について全て整数なら、pCk も整数であることになります。p = 1 のとき、1C0 = 1C1 = 1 なので、帰納法により pCk は整数であることが証明されます。もちろん、p が素数でなくてもこれは成り立ちます。
例によって合っている保証はありません。
今回は、「マテマティカ2」からの問題を解いてみました。ちょっと前からいろいろと解き方を考えていましたが、ようやく解法が見つかりました (正解しているかはわかりませんが)。
-----
153: 複素数
p を素数、a, b を互いに素である自然数とする。( a + bi )^p が実数をとるような a, b, p の組み合わせは何組あるか。ただし、i は虚数単位とする。
二項定理より
( a + bi )p = ap + pC1ap-1・bi + ... + pCkap-k・(bi)k + ... + pCp(bi)p
なので、虚部は bi の指数が奇数の部分で表されます。p = 2 のときは
( a + bi )2 = ( a2 - b2 ) + 2abi
なので、これが実数となるためには ab = 0 である必要がありこれは成り立ちません。従って、p は奇素数の場合だけを考えればよいことになります。任意の奇素数に対し、その虚部は
[ pC1ap-1・b - pC3ap-3・b3 + ... + (-1)(k-1)/2pCkap-k・bk + ... + (-1)(p-1)/2pCpbp ]i
= i・Σk{1→(p+1)/2}( (-1)k-1pC2k-1ap-2k+1・b2k-1 )
となります。従って、これがゼロになれば、( a + bi )p は実数となります。虚数 i を除いて係数部分だけとし、b ≠ 0 より、b で割ると
pC1ap-1 - pC3ap-3・b2 + ... + (-1)(k-1)/2pCkap-k・bk-1 + ... + (-1)(p-1)/2pCpbp-1
= pC1ap-1 - pC3ap-3・b2 + ... + (-1)(k-1)/2pCkap-k・bk-1 + ... + (-1)(p-1)/2bp-1
= 0
より
pC1ap-1 - pC3ap-3・b2 + ... + (-1)(k-1)/2pCkap-k・bk-1 + ... + (-1)(p-3)/2pCp-2a2・bp-3 = -(-1)(p-1)/2bp-1
となりますが、p > k > 0 ならば pCk は必ず p の倍数となるので(証明は後述)、左辺は p の倍数となり、従って右辺にある b は p を素因数に持つ必要があります (左辺がゼロの場合 b = 0 となるのでこの場合は無視できます)。そこで今度は b = pc とすると、
pC1ap-1 - pC3ap-3・(pc)2 + ... + (-1)(k-1)/2pCkap-k・(pc)k-1 + ... + (-1)(p-1)/2(pc)p-1
= pC1ap-1 - p2pC3ap-3・c2 + ... + (-1)(k-1)/2pk-1pCkap-k・ck-1 + ...
+ (-1)(p-1)/2pp-1cp-1
= 0
より
-p2pC3ap-3・c2 + ... + (-1)(k-1)/2pk-1pCkap-k・ck-1 + ... + (-1)(p-1)/2pp-1cp-1 = -pC1ap-1
となり、両辺を p で割れば
-ppC3ap-3・c2 + ... + (-1)(k-1)/2pk-2pCkap-k・ck-1 + ... + (-1)(p-1)/2pp-2cp-1 = -ap-1
なので a も p を素因数として持つことになり、a, b が互いに素であるという仮定に反します。従って、( a + bi )p が実数となるような ( a, b, p ) の組み合わせは存在しないということになります。
p > k > 0 ならば pCk は必ず p の倍数となることの証明ですが、
pCk = p! / k!・( p - k )! = p・( p - 1 )・...・( p - k + 1 ) / k・( k - 1 )・...・2・1
より p が素数で p > k ならば、分母の 1 から k までの数で p を割ることはできないので、pCk が整数なら p はそのまま素因数として残ることになり、従って pCk は p の倍数となります。pCk が整数であることの証明は(組み合わせを表すので当然ではありますが)、
p-1Ck + p-1Ck-1
= ( p - 1 )! / k!・( p - k - 1 )! + ( p - 1 )! / ( k - 1 )!・( p - k )!
= [ ( p - 1 )! / ( k - 1 )!・( p - k - 1 )! ][ 1 / k + 1 / ( p - k ) ]
= [ ( p - 1 )! / ( k - 1 )!・( p - k - 1 )! ]{ [ ( p - k ) + k ] / k( p - k ) ]
= [ ( p - 1 )! / ( k - 1 )!・( p - k - 1 )! ][ p / k( p - k ) ]
= p! / k!・( p - k )! = pCk
より、pCk は p-1Ck + p-1Ck-1 の和で表すことができます。従って、p-1Ck が任意の k について全て整数なら、pCk も整数であることになります。p = 1 のとき、1C0 = 1C1 = 1 なので、帰納法により pCk は整数であることが証明されます。もちろん、p が素数でなくてもこれは成り立ちます。
例によって合っている保証はありません。
2015年09月27日
十五夜を見ながら一問
今日は空も晴れて満月がきれいです。
写真に撮ってみましたが、あまりきれいには写らないですね。

やっぱり、天体望遠鏡がほしくなってくるこの頃です。
「数学問題bot」から、図形の問題にチャレンジです。
-----
3 以上の自然数 n に対して、一辺の長さが 1 の正方形に含まれる面積最大の正 n 角形の面積を Sn とする。S3 と S6 を求めよ。( 近畿大学第 9 回数学コンテスト )
正三角形の面積は一辺の長さによって大小関係が決まります。正方形の中にできるだけ長い辺を持った正三角形が収まるように配置すればいいわけですが、正三角形の少なくとも二つの頂点が正三角形の辺に接するように配置する方が大きくなるのは明らかです。そのような配置の仕方で一辺だけが正方形内に入るようにしたとき、その最小は正三角形の一辺が正方形の一辺に接する配置の仕方で、最大は正方形の対角線が正三角形の一辺になるような配置の仕方です。
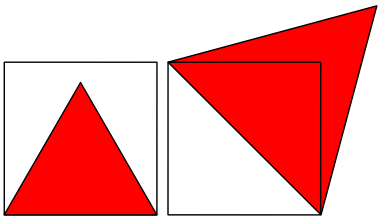
しかし、最小となる配置の場合はもう一つの頂点が正方形の内部にあり、まだ大きくする余地があります。逆に最大となる配置はもう一つの頂点が正方形の外側にあるので条件を満たしません。そこで、正方形と正三角形の頂点が重なっているところを一点だけ選んで固定し、もう一点は正方形の辺上を移動させます。最小となる配置の場合、正三角形はだんだん大きくなり、逆に最大の場合は小さくなっていきます。やがて、もう一つの頂点が正方形の辺上に位置することになります。
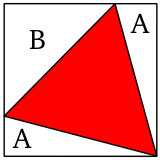
上図の二つの三角形 A は直角三角形で、斜辺は正三角形の辺、もう一辺が正方形の辺なので二つは合同です。従って三角形 B は直角二等辺三角形となります。三角形 A の一つの鋭角は 15 度なので、短い方の辺の長さは sin 15 度になります。これを x とすれば三角形 A の面積は x / 2、三角形 B の面積は ( 1 - x )2 / 2 です。よって、
S3
= 1 - ( x / 2 ) x 2 - ( 1 - x )2 / 2
= ( 1 - x )[ 1 - ( 1 - x ) / 2 ]
= ( 1 - x )( 1 + x ) / 2
= ( 1 - x2 ) / 2
となります。
cos 2θ = 1 - 2sin2θ
より
x2 = ( 1 - cos 30度 ) / 2 = ( 1 - √3 / 2 ) / 2
となって、
S3 = [ 1 - ( 1 - √3 / 2 ) / 2 ] / 2 = 1 / 4 + √3 / 8
となります。
S6 については、次の図を見ればわかりやすいかと思います。
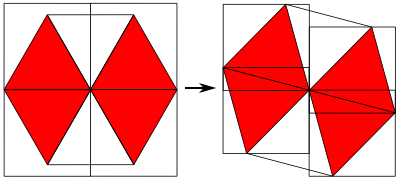
但し、小さい正方形の一辺は 1 / 2 なので、一つの三角形の面積は S3 の 1 / 4 となります。よって、
S6 = S3 x 6 / 4 = 3 / 8 + 3√3 / 16
となります。
例によって、合っているという保証なしです。
写真に撮ってみましたが、あまりきれいには写らないですね。

やっぱり、天体望遠鏡がほしくなってくるこの頃です。
「数学問題bot」から、図形の問題にチャレンジです。
-----
3 以上の自然数 n に対して、一辺の長さが 1 の正方形に含まれる面積最大の正 n 角形の面積を Sn とする。S3 と S6 を求めよ。( 近畿大学第 9 回数学コンテスト )
正三角形の面積は一辺の長さによって大小関係が決まります。正方形の中にできるだけ長い辺を持った正三角形が収まるように配置すればいいわけですが、正三角形の少なくとも二つの頂点が正三角形の辺に接するように配置する方が大きくなるのは明らかです。そのような配置の仕方で一辺だけが正方形内に入るようにしたとき、その最小は正三角形の一辺が正方形の一辺に接する配置の仕方で、最大は正方形の対角線が正三角形の一辺になるような配置の仕方です。

しかし、最小となる配置の場合はもう一つの頂点が正方形の内部にあり、まだ大きくする余地があります。逆に最大となる配置はもう一つの頂点が正方形の外側にあるので条件を満たしません。そこで、正方形と正三角形の頂点が重なっているところを一点だけ選んで固定し、もう一点は正方形の辺上を移動させます。最小となる配置の場合、正三角形はだんだん大きくなり、逆に最大の場合は小さくなっていきます。やがて、もう一つの頂点が正方形の辺上に位置することになります。

上図の二つの三角形 A は直角三角形で、斜辺は正三角形の辺、もう一辺が正方形の辺なので二つは合同です。従って三角形 B は直角二等辺三角形となります。三角形 A の一つの鋭角は 15 度なので、短い方の辺の長さは sin 15 度になります。これを x とすれば三角形 A の面積は x / 2、三角形 B の面積は ( 1 - x )2 / 2 です。よって、
S3
= 1 - ( x / 2 ) x 2 - ( 1 - x )2 / 2
= ( 1 - x )[ 1 - ( 1 - x ) / 2 ]
= ( 1 - x )( 1 + x ) / 2
= ( 1 - x2 ) / 2
となります。
cos 2θ = 1 - 2sin2θ
より
x2 = ( 1 - cos 30度 ) / 2 = ( 1 - √3 / 2 ) / 2
となって、
S3 = [ 1 - ( 1 - √3 / 2 ) / 2 ] / 2 = 1 / 4 + √3 / 8
となります。
S6 については、次の図を見ればわかりやすいかと思います。

但し、小さい正方形の一辺は 1 / 2 なので、一つの三角形の面積は S3 の 1 / 4 となります。よって、
S6 = S3 x 6 / 4 = 3 / 8 + 3√3 / 16
となります。
例によって、合っているという保証なしです。
2015年08月22日
解と係数の不思議な関係
気がつけば、夏休みも残り一週間あまりとなりました。
天むすは名古屋が発祥の地と思っていましたが、実際は三重県の津市なんだそうです。本当に知りませんでした。名古屋の人にウケたからそう勘違いされるようになったんでしょうかね。しかし、自分はあまり食べたことないです。エビフライも特別好きというわけではないし。
「マテマティカ2」さんからまた一問挑戦。例によって合っている保証はありません。
-----
方程式
x17 + 7x = 1 (☆)
について、
(1) ☆の 17 個の解の 17 乗の総和を求めよ。
(2) ☆の 17 個の解の逆数の和を求めよ。
( x - a )( x - b ) = x2 - ( a + b )x + ab より、二次方程式 x2 + Ax + B = 0 の解と係数の関係は
A = -( a + b )
B = ab
となります。これは、たしか高校時代に習った内容だったと記憶しています。
二次方程式の左辺に x - c を掛けた三次式
[ x2 - ( a + b )x + ab ]( x - c )
の二次項は、左側カッコ内の式の一次項 -( a + b )x と右側カッコ内の式の一次項 x の積と、同様に左側二次項 x2 と右側定数項 -c の積の和となるので係数は -( a + b + c ) となり、二次項の係数は解の和の符号を反転したものと等しくなります。N 次方程式の N - 1 次項の係数が同様に解の和の符号を反転したものに等しい、すなわち
Πi{1→N}( x - ai ) = xN - Σi{1→N}aixN-1 + R(x)
但し R(x) は N - 2 次以下の項の和
と仮定したとき、この式に x - aN+1 を掛けて展開すると、N 次項は、左側カッコ内の式の N - 1 次項 -Σi{1→N}aixN-1 と右側カッコ内の式の一次項 x の積と、左側 N 次項 xN と右側定数項 -aN+1 の積の和となるので係数は -Σi{1→N+1}ai となり、N 次項の係数も解の和の符号を反転したものに等しくなります。よって帰納法により、任意の自然数 N に対し、N 次項の係数が 1 である N 次方程式の係数は解の和の符号を反転したものに等しくなります。
方程式 x17 + 7x = 1 に対し、16 次項は存在しない(係数はゼロ)ことから解の和はゼロになります。任意の解について x17 = 1 - 7x なので、解 x を 17 乗した値の和は 1 - 7x の和に等しくなります。ところが 7x の和はゼロになるので、和は 17 となります。
同様に一次項について考察すると、三次式においては左側定数項 ab と右側一次項 x の積と、左側一次項 -( a + b )x と右側定数項 -c の積の和になるので係数は
( a + b )c + ab = bc + ca + ab = abc( 1/a + 1/b + 1/c )
になります。また、定数項は -abc であることはすぐに分かります。そこで N 次方程式が
Πi{1→N}( x - ai ) = xN + ( -1 )N+1Πi{1→N}aiΣi{1→N}( 1 / ai )x + ( -1 )NΠi{1→N}ai + R(x)
但し R(x) は 2 次から N - 2 次までの項の和
と仮定してみます。これに x - aN+1 を掛けて展開すると、一次項は、左側定数項 ( -1 )NΠi{1→N}ai と右側一次項 x の積と、左側一次項 ( -1 )N+1Πi{1→N}aiΣi{1→N}( 1 / ai )x と右側定数項 -aN+1 の積の和になるので係数は
( -1 )NΠi{1→N}ai + ( -aN+1 )( -1 )N+1Πi{1→N}aiΣi{1→N}( 1 / ai )
= ( -1 )N+2( 1 / aN+1 )Πi{1→N+1}ai + ( -1 )N+2Πi{1→N+1}aiΣi{1→N}( 1 / ai )
= ( -1 )N+2Πi{1→N+1}aiΣi{1→N+1}( 1 / ai )
であり、帰納法によって、任意の N に対して一次項の係数が ( -1 )N+1Πi{1→N}aiΣi{1→N}( 1 / ai ) となることが示されます。同様に、定数項が ( -1 )NΠi{1→N}ai で表されることは簡単に示すことができるので、この二つを使うと解の逆数の和は一次項の係数を定数項で割って符号を逆転することで求めることができます。
方程式 x17 + 7x - 1 = 0 の一次項は 7、定数項は -1 なので、解の逆数の和は -( 7 / -1 ) = 7 となります。
多項式の解と係数の関係を利用した問題ですね。最初はどこから手を付ければよいかなかなか気づかず苦戦しました。
天むすは名古屋が発祥の地と思っていましたが、実際は三重県の津市なんだそうです。本当に知りませんでした。名古屋の人にウケたからそう勘違いされるようになったんでしょうかね。しかし、自分はあまり食べたことないです。エビフライも特別好きというわけではないし。
「マテマティカ2」さんからまた一問挑戦。例によって合っている保証はありません。
-----
方程式
x17 + 7x = 1 (☆)
について、
(1) ☆の 17 個の解の 17 乗の総和を求めよ。
(2) ☆の 17 個の解の逆数の和を求めよ。
( x - a )( x - b ) = x2 - ( a + b )x + ab より、二次方程式 x2 + Ax + B = 0 の解と係数の関係は
A = -( a + b )
B = ab
となります。これは、たしか高校時代に習った内容だったと記憶しています。
二次方程式の左辺に x - c を掛けた三次式
[ x2 - ( a + b )x + ab ]( x - c )
の二次項は、左側カッコ内の式の一次項 -( a + b )x と右側カッコ内の式の一次項 x の積と、同様に左側二次項 x2 と右側定数項 -c の積の和となるので係数は -( a + b + c ) となり、二次項の係数は解の和の符号を反転したものと等しくなります。N 次方程式の N - 1 次項の係数が同様に解の和の符号を反転したものに等しい、すなわち
Πi{1→N}( x - ai ) = xN - Σi{1→N}aixN-1 + R(x)
但し R(x) は N - 2 次以下の項の和
と仮定したとき、この式に x - aN+1 を掛けて展開すると、N 次項は、左側カッコ内の式の N - 1 次項 -Σi{1→N}aixN-1 と右側カッコ内の式の一次項 x の積と、左側 N 次項 xN と右側定数項 -aN+1 の積の和となるので係数は -Σi{1→N+1}ai となり、N 次項の係数も解の和の符号を反転したものに等しくなります。よって帰納法により、任意の自然数 N に対し、N 次項の係数が 1 である N 次方程式の係数は解の和の符号を反転したものに等しくなります。
方程式 x17 + 7x = 1 に対し、16 次項は存在しない(係数はゼロ)ことから解の和はゼロになります。任意の解について x17 = 1 - 7x なので、解 x を 17 乗した値の和は 1 - 7x の和に等しくなります。ところが 7x の和はゼロになるので、和は 17 となります。
同様に一次項について考察すると、三次式においては左側定数項 ab と右側一次項 x の積と、左側一次項 -( a + b )x と右側定数項 -c の積の和になるので係数は
( a + b )c + ab = bc + ca + ab = abc( 1/a + 1/b + 1/c )
になります。また、定数項は -abc であることはすぐに分かります。そこで N 次方程式が
Πi{1→N}( x - ai ) = xN + ( -1 )N+1Πi{1→N}aiΣi{1→N}( 1 / ai )x + ( -1 )NΠi{1→N}ai + R(x)
但し R(x) は 2 次から N - 2 次までの項の和
と仮定してみます。これに x - aN+1 を掛けて展開すると、一次項は、左側定数項 ( -1 )NΠi{1→N}ai と右側一次項 x の積と、左側一次項 ( -1 )N+1Πi{1→N}aiΣi{1→N}( 1 / ai )x と右側定数項 -aN+1 の積の和になるので係数は
( -1 )NΠi{1→N}ai + ( -aN+1 )( -1 )N+1Πi{1→N}aiΣi{1→N}( 1 / ai )
= ( -1 )N+2( 1 / aN+1 )Πi{1→N+1}ai + ( -1 )N+2Πi{1→N+1}aiΣi{1→N}( 1 / ai )
= ( -1 )N+2Πi{1→N+1}aiΣi{1→N+1}( 1 / ai )
であり、帰納法によって、任意の N に対して一次項の係数が ( -1 )N+1Πi{1→N}aiΣi{1→N}( 1 / ai ) となることが示されます。同様に、定数項が ( -1 )NΠi{1→N}ai で表されることは簡単に示すことができるので、この二つを使うと解の逆数の和は一次項の係数を定数項で割って符号を逆転することで求めることができます。
方程式 x17 + 7x - 1 = 0 の一次項は 7、定数項は -1 なので、解の逆数の和は -( 7 / -1 ) = 7 となります。
多項式の解と係数の関係を利用した問題ですね。最初はどこから手を付ければよいかなかなか気づかず苦戦しました。
2015年08月14日
モニタ故障(その後)
テレビをモニタ代わりに使うのはきついので、以前使っていたノート PC からリモートでアクセスできるようにしました。これで休日の一日がつぶれてしまいました。
メイン PC は現在 Windows7 がホスト OS で、ここに VirtualBox を入れて Vine Linux をゲスト OS に使っています。
Windows7 へは vnc でアクセスできるようにしたものの、動作が重すぎてこちらは使い物になりませんでした。VirtualBox のゲスト OS にリモートデスクトップ接続できることを知って試してみたのですが接続ができず、よくよく調べてみると拡張パックをインストールしなければならないということで、さっそくダウンロード。Ver5 がリリースされていたということでついでにバージョンアップもしました。これで Linux へもアクセスできるようになり、しかもこちらは充分利用可能だったので何とかしのぐことができました。ちなみにノート PC は Lenovo の ThinkPad T510 という機種。中には xubuntu が入っていて、ずっと使ってなかったのでアップグレードも実施しました。
それから、購入するモニタの目処はついたものの、二台のうちからまだ選べきれず、悩んでいます。
いつ、どこで拾ったのか思い出せないですが、どこかの大学の入試問題だと記憶してます。
-----
t をパラメータとする次の曲線の法平面は原点で交わることを証明せよ。 x = a sin2 t, y = a sin t cos t , z = a cos t
まずは ( x, y, z ) を t で微分してみます。
dx / dt = 2a sin t cos t = a sin 2t
dy / dt = a cos2 t - a sin2 t = a cos 2t
dz / dt = -a sin t
∇ = ( dx/dt, dy/dt, dz/dt ) としたとき、∇ は曲線の接線ベクトルを表すので、その法平面は
a sin 2t ( x - a sin2 t ) + a cos 2t ( y - a sin t cos t ) - a sin t ( z - a cos t ) = 0
となります。( x, y, z ) = 0 のとき左辺は
-a sin 2t・a sin2 t - a cos 2t・a sin t cos t + a sin t・a cos t
= -a2 sin 2t・sin2 t - ( a2 / 2 ) cos 2t・sin 2t + ( a2 / 2 ) sin 2t
= -a2 sin 2t・sin2 t + ( a2 / 2 ) sin 2t ( 1 - cos 2t )
= -a2 sin 2t・sin2 t + ( a2 / 2 ) sin 2t [ 1 - ( cos2 t - sin2 t ) ]
= -a2 sin 2t・sin2 t + ( a2 / 2 ) sin 2t・2sin2 t
= -a2 sin 2t・sin2 t + a2 sin 2t・sin2 t = 0
であり、任意の t について曲線の法平面は原点で交わります。
例によって合っている保証はありません。
メイン PC は現在 Windows7 がホスト OS で、ここに VirtualBox を入れて Vine Linux をゲスト OS に使っています。
Windows7 へは vnc でアクセスできるようにしたものの、動作が重すぎてこちらは使い物になりませんでした。VirtualBox のゲスト OS にリモートデスクトップ接続できることを知って試してみたのですが接続ができず、よくよく調べてみると拡張パックをインストールしなければならないということで、さっそくダウンロード。Ver5 がリリースされていたということでついでにバージョンアップもしました。これで Linux へもアクセスできるようになり、しかもこちらは充分利用可能だったので何とかしのぐことができました。ちなみにノート PC は Lenovo の ThinkPad T510 という機種。中には xubuntu が入っていて、ずっと使ってなかったのでアップグレードも実施しました。
それから、購入するモニタの目処はついたものの、二台のうちからまだ選べきれず、悩んでいます。
いつ、どこで拾ったのか思い出せないですが、どこかの大学の入試問題だと記憶してます。
-----
t をパラメータとする次の曲線の法平面は原点で交わることを証明せよ。 x = a sin2 t, y = a sin t cos t , z = a cos t
まずは ( x, y, z ) を t で微分してみます。
dx / dt = 2a sin t cos t = a sin 2t
dy / dt = a cos2 t - a sin2 t = a cos 2t
dz / dt = -a sin t
∇ = ( dx/dt, dy/dt, dz/dt ) としたとき、∇ は曲線の接線ベクトルを表すので、その法平面は
a sin 2t ( x - a sin2 t ) + a cos 2t ( y - a sin t cos t ) - a sin t ( z - a cos t ) = 0
となります。( x, y, z ) = 0 のとき左辺は
-a sin 2t・a sin2 t - a cos 2t・a sin t cos t + a sin t・a cos t
= -a2 sin 2t・sin2 t - ( a2 / 2 ) cos 2t・sin 2t + ( a2 / 2 ) sin 2t
= -a2 sin 2t・sin2 t + ( a2 / 2 ) sin 2t ( 1 - cos 2t )
= -a2 sin 2t・sin2 t + ( a2 / 2 ) sin 2t [ 1 - ( cos2 t - sin2 t ) ]
= -a2 sin 2t・sin2 t + ( a2 / 2 ) sin 2t・2sin2 t
= -a2 sin 2t・sin2 t + a2 sin 2t・sin2 t = 0
であり、任意の t について曲線の法平面は原点で交わります。
例によって合っている保証はありません。
2015年08月08日
立秋
今日から暦の上では秋になります。まだまだ暑い日が続きそうですが、今日は少しだけ涼しかったような気がします。
Twitter で数学の問題を出題しているサイトをまた見つけました。というか、フォローされていて気付かなかったようで、今日ようやくフォローいたしました。マテマティカ2 というユーザさんで、その中から一問挑戦してみました。
-----
143: 集合 M は 3 つの元 0, i, j からなる。すなわち M = { 0, i, j } である。M で加法をどのように定義すると、交換法則、結合法則を満たし、かつ減法できるようになるか。
また、上のときの次の計算をせよ。
i + i
i + j
j + j
ただし、任意の k に対して、k + 0 = k とする。
(解) 任意の k に対して k + 0 = k なので、0 + 0 = 0, i + 0 = 0 + i = i, j + 0 = 0 + j = j です。
また、i + j = i の場合 j = 0 となり、i + j = j の場合は i = 0 となるため、i + j = 0 でなければなりません。従って、
i = 0 - j = -j
j = 0 - i = -i
となります。結合法則を満たすためには、
( i + i ) + j = i + ( i + j )
が成り立つ必要がありますが、右辺は i に等しくなるため
( i + i ) + j = i より i + i = i - j = -j - j = -( j + j )
です。同様に
( j + j ) + i = j より j + j = j - i = -i - i = -( i + i )
となります。
つまり、i は j の ( j は i の ) 逆元になるように加法を定義すればよいということになります。
例によって合っている保証はないので注意です。
Twitter で数学の問題を出題しているサイトをまた見つけました。というか、フォローされていて気付かなかったようで、今日ようやくフォローいたしました。マテマティカ2 というユーザさんで、その中から一問挑戦してみました。
-----
143: 集合 M は 3 つの元 0, i, j からなる。すなわち M = { 0, i, j } である。M で加法をどのように定義すると、交換法則、結合法則を満たし、かつ減法できるようになるか。
また、上のときの次の計算をせよ。
i + i
i + j
j + j
ただし、任意の k に対して、k + 0 = k とする。
(解) 任意の k に対して k + 0 = k なので、0 + 0 = 0, i + 0 = 0 + i = i, j + 0 = 0 + j = j です。
また、i + j = i の場合 j = 0 となり、i + j = j の場合は i = 0 となるため、i + j = 0 でなければなりません。従って、
i = 0 - j = -j
j = 0 - i = -i
となります。結合法則を満たすためには、
( i + i ) + j = i + ( i + j )
が成り立つ必要がありますが、右辺は i に等しくなるため
( i + i ) + j = i より i + i = i - j = -j - j = -( j + j )
です。同様に
( j + j ) + i = j より j + j = j - i = -i - i = -( i + i )
となります。
つまり、i は j の ( j は i の ) 逆元になるように加法を定義すればよいということになります。
例によって合っている保証はないので注意です。
2015年07月05日
今年も残り半分
七月になりました。もう今年も半分終わったんですね。
そしてこれから本格的に夏が始まります。一番好きな季節です。暑いのはイヤですが。
しかし、今年は雨が多いような気がします。気温もそんなに高くはないし、例年よりは過ごし易いのではないかと感じています。これくらいの状態が続いてくれればかなり楽なんですけどね。いや、大雨だけは勘弁してほしいですが。
久しぶりに「数学問題bot」から京大の問題に挑戦。
-----
Q(x)を2次式とする。整式P(x)はQ(x)では割り切れないが、[P(x)]^2はQ(x)で割り切れるという。このとき二次方程式Q(x)=0は重解を持つことを示せ(06京都)
Q(x) = 0 の解を x = a, b とします。但し a, b は複素数までの範囲を取るものとします。
a ≠ b と仮定します。P(x) は Q(x) で割り切れないので、x = a, b のいずれかを P(x) = 0 の解として持たない、すなわち P(a) ≠ 0 または P(b) ≠ 0 が成り立つことになります。このとき、[P(a)]^2 = 0 と [P(b)]^2 = 0 が同時に成り立つことはなく、x - a, x - b のいずれかを因子として持たないことになり、Q(x) では割り切れません。よって、Q(x) = 0 が重解を持たないとき、P(x) が Q(x) で割り切れず、同時に [P(x)]^2 が Q(x) で割り切れるということはありません。その対偶として P(x) が Q(x)で割り切れず、[P(x)]^2 が Q(x)で割り切れる場合は Q(x) = 0 が重解を持つ時しかありません。
具体的には、P(x) が Q(x) = 0 の重解を一つだけ持つ場合、P(x) が Q(x) で割り切れず [P(x)]^2 が Q(x)で割り切れます。
実は解いてみた後で結果が当たり前のような気がして、何かとんでもない勘違いをしているのではないかと思い、今回は他のサイトで回答を探してみました。一応、合ってはいるようですが、もっとわかりやすい方法で解いていたのも見つけたので、あまり模範的な解き方ではないようです。
そしてこれから本格的に夏が始まります。一番好きな季節です。暑いのはイヤですが。
しかし、今年は雨が多いような気がします。気温もそんなに高くはないし、例年よりは過ごし易いのではないかと感じています。これくらいの状態が続いてくれればかなり楽なんですけどね。いや、大雨だけは勘弁してほしいですが。
久しぶりに「数学問題bot」から京大の問題に挑戦。
-----
Q(x)を2次式とする。整式P(x)はQ(x)では割り切れないが、[P(x)]^2はQ(x)で割り切れるという。このとき二次方程式Q(x)=0は重解を持つことを示せ(06京都)
Q(x) = 0 の解を x = a, b とします。但し a, b は複素数までの範囲を取るものとします。
a ≠ b と仮定します。P(x) は Q(x) で割り切れないので、x = a, b のいずれかを P(x) = 0 の解として持たない、すなわち P(a) ≠ 0 または P(b) ≠ 0 が成り立つことになります。このとき、[P(a)]^2 = 0 と [P(b)]^2 = 0 が同時に成り立つことはなく、x - a, x - b のいずれかを因子として持たないことになり、Q(x) では割り切れません。よって、Q(x) = 0 が重解を持たないとき、P(x) が Q(x) で割り切れず、同時に [P(x)]^2 が Q(x) で割り切れるということはありません。その対偶として P(x) が Q(x)で割り切れず、[P(x)]^2 が Q(x)で割り切れる場合は Q(x) = 0 が重解を持つ時しかありません。
具体的には、P(x) が Q(x) = 0 の重解を一つだけ持つ場合、P(x) が Q(x) で割り切れず [P(x)]^2 が Q(x)で割り切れます。
実は解いてみた後で結果が当たり前のような気がして、何かとんでもない勘違いをしているのではないかと思い、今回は他のサイトで回答を探してみました。一応、合ってはいるようですが、もっとわかりやすい方法で解いていたのも見つけたので、あまり模範的な解き方ではないようです。
2015年05月24日
もうすぐ名古屋場所
大相撲夏場所は照ノ富士が大混戦を制しました。
白鵬が優勝を逃してしまいましたね。日馬富士が白鵬を破ったあと、照ノ富士が大泣きしていたのが印象的でした。次は名古屋場所ですが、名古屋場所が始まると、本格的な夏が到来したという気分になります。今度はどんな展開になるか楽しみですね。
「数学問題bot」からこんな問題を選んでみました。
-----
1 から 10 までの整数が 1 つずつ書かれた 10 枚のカードがある。この中からカードを 3 枚同時に取り出す。取り出された 3 枚のカードに書かれた 3 つの整数のうち最大のものを除いた残りの 2 つの整数の和を X とする。(中略) X の期待値を求めよ。( 06 千葉・理 )
3 枚のカードの中に 1, 2 が含まれる場合の数は残りのカードが 3 から 10 までの 8 通りあり、この時 X = 1 + 2 = 3 です。1 を固定して 2 のカードを任意 ( M = 2 ~ 9 ) としたとき、残りのカードは 10 - M 通りの場合があり、X = 1 + M です。さらに 1 のカードも任意 ( L = 1 ~ M - 1 ) とすれば、残りのカードの取る場合の数は変わらず X = L + M となります。このことから、X の総和は
ΣM{2→9}( ΣL{1→M-1}( ( L + M )( 10 - M ) ) )
で計算できます。式を変形して
ΣM{2→9}( ΣL{1→M-1}( ( L + M )( 10 - M ) ) )
=ΣM{2→9}( ( 10 - M )ΣL{1→M-1}( L + M ) )
=ΣM{2→9}( ( 10 - M )[ M( M - 1 ) / 2 + M( M - 1 ) ] )
=ΣM{2→9}( 3M( M - 1 )( 10 - M ) / 2 )
= 24 + 63 + 108 + 150 + 180 + 189 + 168 + 108 = 990
10 枚のカードから 3 枚を選ぶ場合の数は 10・9・8 / 3・2 = 120 通りなので、期待値は
990 / 120 = 33 / 4
になります。
*例によって合っている保証なしです。会社の行き帰りに何となく考えていたら解法が浮かんできました。
白鵬が優勝を逃してしまいましたね。日馬富士が白鵬を破ったあと、照ノ富士が大泣きしていたのが印象的でした。次は名古屋場所ですが、名古屋場所が始まると、本格的な夏が到来したという気分になります。今度はどんな展開になるか楽しみですね。
「数学問題bot」からこんな問題を選んでみました。
-----
1 から 10 までの整数が 1 つずつ書かれた 10 枚のカードがある。この中からカードを 3 枚同時に取り出す。取り出された 3 枚のカードに書かれた 3 つの整数のうち最大のものを除いた残りの 2 つの整数の和を X とする。(中略) X の期待値を求めよ。( 06 千葉・理 )
3 枚のカードの中に 1, 2 が含まれる場合の数は残りのカードが 3 から 10 までの 8 通りあり、この時 X = 1 + 2 = 3 です。1 を固定して 2 のカードを任意 ( M = 2 ~ 9 ) としたとき、残りのカードは 10 - M 通りの場合があり、X = 1 + M です。さらに 1 のカードも任意 ( L = 1 ~ M - 1 ) とすれば、残りのカードの取る場合の数は変わらず X = L + M となります。このことから、X の総和は
ΣM{2→9}( ΣL{1→M-1}( ( L + M )( 10 - M ) ) )
で計算できます。式を変形して
ΣM{2→9}( ΣL{1→M-1}( ( L + M )( 10 - M ) ) )
=ΣM{2→9}( ( 10 - M )ΣL{1→M-1}( L + M ) )
=ΣM{2→9}( ( 10 - M )[ M( M - 1 ) / 2 + M( M - 1 ) ] )
=ΣM{2→9}( 3M( M - 1 )( 10 - M ) / 2 )
= 24 + 63 + 108 + 150 + 180 + 189 + 168 + 108 = 990
10 枚のカードから 3 枚を選ぶ場合の数は 10・9・8 / 3・2 = 120 通りなので、期待値は
990 / 120 = 33 / 4
になります。
*例によって合っている保証なしです。会社の行き帰りに何となく考えていたら解法が浮かんできました。
2015年05月15日
円周率
今日は暑いですね。湿度も高くてジメッとしてます。
東大の入試問題でおもしろいのを見つけました。
-----
円周率が 3.05 より大きいことを証明せよ。( 03 東大 )
円周率の近似値を求める方法はいろいろありますが、一番素朴な方法で解いてみました。
半径 1 の円の円周は 2π です。この円に内接する正六角形は、円の中心から各頂点へ結んだ線からできる六つの三角形が全て正三角形になることから明らかなように一辺が 1 になります。従って、その周は 6 になります。二点を結ぶ線は直線の時に最小となることから、正六角形の周より円周の方が大きいので
2π > 6 より π > 3
が成り立ち、円周率は 3 より大きいことがわかります。
頂点の数を倍にして正 12 角形の場合を考えます。円の中心から各頂点へ結んだ線からできる 12 個の二等辺三角形の頂角は 30 度で、底辺に垂線を下ろした時は半分の 15 度です。斜辺の長さは 1 なので、三角形の底辺は 2sin15° で求められます。倍角の公式から
cos215° - sin215°= cos30°= √3/2
で、
cos215° + sin215°= 1
なので、下式から上式を辺々引くと
2sin215° = 1 - √3/2 より
sin15°= ( 2 - √3 )1/2 / 2
となります。√3 < 1.733 なので、
( 2 - √3 )1/2 > 0.2671/2 > 0.510
となり、三角形の底辺は 0.510 より大きいので、正 12 角形の周の長さは 12 x 0.510 = 6.12 より大きく、円周はそれより大きいので
2π > 6.12 より π > 3.06
が成り立ち、証明ができました。
東大の入試問題でおもしろいのを見つけました。
-----
円周率が 3.05 より大きいことを証明せよ。( 03 東大 )
円周率の近似値を求める方法はいろいろありますが、一番素朴な方法で解いてみました。
半径 1 の円の円周は 2π です。この円に内接する正六角形は、円の中心から各頂点へ結んだ線からできる六つの三角形が全て正三角形になることから明らかなように一辺が 1 になります。従って、その周は 6 になります。二点を結ぶ線は直線の時に最小となることから、正六角形の周より円周の方が大きいので
2π > 6 より π > 3
が成り立ち、円周率は 3 より大きいことがわかります。
頂点の数を倍にして正 12 角形の場合を考えます。円の中心から各頂点へ結んだ線からできる 12 個の二等辺三角形の頂角は 30 度で、底辺に垂線を下ろした時は半分の 15 度です。斜辺の長さは 1 なので、三角形の底辺は 2sin15° で求められます。倍角の公式から
cos215° - sin215°= cos30°= √3/2
で、
cos215° + sin215°= 1
なので、下式から上式を辺々引くと
2sin215° = 1 - √3/2 より
sin15°= ( 2 - √3 )1/2 / 2
となります。√3 < 1.733 なので、
( 2 - √3 )1/2 > 0.2671/2 > 0.510
となり、三角形の底辺は 0.510 より大きいので、正 12 角形の周の長さは 12 x 0.510 = 6.12 より大きく、円周はそれより大きいので
2π > 6.12 より π > 3.06
が成り立ち、証明ができました。
2015年04月19日
明日は雨のようです
現在、確率・統計用サンプル・プログラムの大幅な見直し中です。
次は「生存時間解析」を新しいテーマとして公開する予定ですが、その前に今までのサンプル・プログラムを見直しておかないと、あまりにもゴチャゴチャになりすぎて収集がつかなくなると思い着手し始めてからだいぶ経ちます。ようやく 1 / 3 程度が完了したところで、まだ先は長いです。一応、整理が済んだら公開をしようと考えています。
久しぶりの数学問題。今回は名古屋大の入試問題です。
-----
サイコロを投げると 1 から 6 までの整数の目が等しい確率で出るとする。サイコロを n 回 ( n = 1, 2, 3, ... ) 投げるとき、出る目の積の 1 の位が j ( j = 0, 1, 2, ... ,9 ) となる確率を P_n(j) とする。(中略) 4) P_n(5) を求めよ。( 09 名古屋・理 )
まず、積の 1 の位が奇数であるためには、出た目の数が全て奇数である必要があるため、一つでも偶数の目が出る場合は全て除外することができます。n - 1 回の試行で 1 の位が奇数であった時、n 回目の試行によって 1 の位が 5 になるためには、n 回目に 5 が出るか、または n - 1 回目で 1 の位が 5 であった場合に限られます。n 回目で 1 の位が奇数となる場合の数は、n = 1 のとき { 1, 3, 5 } で 3 通りであり、n = 2 のとき、各場合に対して奇数の目が出る場合の数はそれぞれ 3 ( 例えば 1 に対して { 1, 1 } { 1, 3 } { 1, 5 } ) なので、32 となります。この操作を繰り返すと、n のときは 3n 通りの場合があることになります。
n - 1 回目では、積の 1 の位が奇数になる場合が 3n-1 通りあり、5 になる場合の数を F_n-1(5) で表すと、n 回目の試行では奇数の時に 5 が出る 3n-1 通りと、5 の時に奇数が出る 3 * F_n-1(5) 通りの場合に 1 の位が 5 になります。しかし、奇数の場合の中には 5 が含まれ、n - 1 回目の時に 1 の位が 5 で、n 回目も 5 が出た場合は重複して数えているため、その場合の数 F_n-1(5) を差し引く必要があります。これらの結果から
F_n(5) = 3n-1 + 3F_n-1(5) - F_n-1(5) = 2F_n-1(5) + 3n-1
という漸化式が得られます。
F_n(5) - 2F_n-1(5) = 3n-1
より
F_n(5) - 2F_n-1(5) = 3n-1
2F_n-1(5) - 22F_n-2(5) = 2・3n-2
22F_n-2(5) - 23F_n-3(5) = 22・3n-3
:
2n-2F_2(5) - 2n-1F_1(5) = 2n-2・3
となるので、辺々加えると
F_n(5) - 2n-1F_1(5) = 3n-1 + 2・3n-2 + 22・3n-3 + ... + 2n-2・3
となります。右辺については
S = 3n-1 + 2・3n-2 + 22・3n-3 + ... + 2n-3・32 + 2n-2・3
とすると
( 2 / 3 )S = 2・3n-2 + 22・3n-3 + 23・3n-4 + ... + 2n-2・3 + 2n-1
なので、辺々差し引くと
( 1 - 2 / 3 )S = 3n-1 - 2n-1
より
S = 3n - 3・2n-1
となります。また、F_1(5) = 1 なので、
F_n(5) = 3n - 3・2n-1 - 2n-1 = 3n - 2n
という結果が得られます。最後に、n 回目の試行で出る目の組み合わせは 6n 通りあるので、
P_n(5) = ( 3n - 2n ) / 6n
となります。
例によって、合っている保証はありません。
それから、5 以外の場合も求めることができるのかというのも気になるところです。時間があればチャレンジしてみたいですね。
次は「生存時間解析」を新しいテーマとして公開する予定ですが、その前に今までのサンプル・プログラムを見直しておかないと、あまりにもゴチャゴチャになりすぎて収集がつかなくなると思い着手し始めてからだいぶ経ちます。ようやく 1 / 3 程度が完了したところで、まだ先は長いです。一応、整理が済んだら公開をしようと考えています。
久しぶりの数学問題。今回は名古屋大の入試問題です。
-----
サイコロを投げると 1 から 6 までの整数の目が等しい確率で出るとする。サイコロを n 回 ( n = 1, 2, 3, ... ) 投げるとき、出る目の積の 1 の位が j ( j = 0, 1, 2, ... ,9 ) となる確率を P_n(j) とする。(中略) 4) P_n(5) を求めよ。( 09 名古屋・理 )
まず、積の 1 の位が奇数であるためには、出た目の数が全て奇数である必要があるため、一つでも偶数の目が出る場合は全て除外することができます。n - 1 回の試行で 1 の位が奇数であった時、n 回目の試行によって 1 の位が 5 になるためには、n 回目に 5 が出るか、または n - 1 回目で 1 の位が 5 であった場合に限られます。n 回目で 1 の位が奇数となる場合の数は、n = 1 のとき { 1, 3, 5 } で 3 通りであり、n = 2 のとき、各場合に対して奇数の目が出る場合の数はそれぞれ 3 ( 例えば 1 に対して { 1, 1 } { 1, 3 } { 1, 5 } ) なので、32 となります。この操作を繰り返すと、n のときは 3n 通りの場合があることになります。
n - 1 回目では、積の 1 の位が奇数になる場合が 3n-1 通りあり、5 になる場合の数を F_n-1(5) で表すと、n 回目の試行では奇数の時に 5 が出る 3n-1 通りと、5 の時に奇数が出る 3 * F_n-1(5) 通りの場合に 1 の位が 5 になります。しかし、奇数の場合の中には 5 が含まれ、n - 1 回目の時に 1 の位が 5 で、n 回目も 5 が出た場合は重複して数えているため、その場合の数 F_n-1(5) を差し引く必要があります。これらの結果から
F_n(5) = 3n-1 + 3F_n-1(5) - F_n-1(5) = 2F_n-1(5) + 3n-1
という漸化式が得られます。
F_n(5) - 2F_n-1(5) = 3n-1
より
F_n(5) - 2F_n-1(5) = 3n-1
2F_n-1(5) - 22F_n-2(5) = 2・3n-2
22F_n-2(5) - 23F_n-3(5) = 22・3n-3
:
2n-2F_2(5) - 2n-1F_1(5) = 2n-2・3
となるので、辺々加えると
F_n(5) - 2n-1F_1(5) = 3n-1 + 2・3n-2 + 22・3n-3 + ... + 2n-2・3
となります。右辺については
S = 3n-1 + 2・3n-2 + 22・3n-3 + ... + 2n-3・32 + 2n-2・3
とすると
( 2 / 3 )S = 2・3n-2 + 22・3n-3 + 23・3n-4 + ... + 2n-2・3 + 2n-1
なので、辺々差し引くと
( 1 - 2 / 3 )S = 3n-1 - 2n-1
より
S = 3n - 3・2n-1
となります。また、F_1(5) = 1 なので、
F_n(5) = 3n - 3・2n-1 - 2n-1 = 3n - 2n
という結果が得られます。最後に、n 回目の試行で出る目の組み合わせは 6n 通りあるので、
P_n(5) = ( 3n - 2n ) / 6n
となります。
例によって、合っている保証はありません。
それから、5 以外の場合も求めることができるのかというのも気になるところです。時間があればチャレンジしてみたいですね。
2015年03月11日
今日は 3 月 11 日 ...
東日本大震災から四年が経過しました。
阪神・淡路大震災のときは早朝に家で、東日本大震災のときは会社で電話中に揺れを感じました。どちらも後でテレビを通じて被害の大きさに気づいたんですよね。原発の事故の様子を見た時は本当に恐ろしかったです。原発の廃炉への道のりは、まだまだかなり長く険しいようです。こんな状況でも原発を推進しようとするというのはやはり考えられないです。
NHK東日本大震災アーカイブス ( http://www9.nhk.or.jp/311shogen/ )
久々に、数学の問題に挑戦。京大の入試問題です。「誘導略」なので全然違う解き方をしているのかもしれません。また、合っている保証もないです。
-----
■ a, b を互いに素な自然数とする。a は奇数とする。自然数 n に対して 整数an, bn を ( a + b√2 )n = an + bn√2 を満たすように定めるとき、an と bn は互いに素であることを示せ( 2009 年京大理系乙誘導略 )
( an + bn√2 )( a + b√2 ) = ( a・an + 2b・bn ) + ( b・an + a・bn )√2 より
an+1 = a・an + 2b・bn
bn+1 = b・an + a・bn
が成り立ちます。an, bn が共通の因数 c を持つならば、an+1, bn+1 も同じ共通の因数 c を持つことになるので、ある値 n で an, bn が互いに素でなくなったら、N > n の任意の N でも an, bn は互いに素ではなくなります。
ところが、an, bn が互いに素であるとき、
( an + bn√2 )2 = ( an2 + 2bn2 ) + 2anbn√2 より
a2n = an2 + 2bn2
b2n = 2anbn
なので、an が奇数ならば an2 と 2bn2 には公約数はなく、a2n は 2, an, bn それぞれの素因数を約数として持ちません。逆に、2anbn は 2, an, bn それぞれの素因数の積しか約数にならないので、a_2n, b_2n は互いに素です。特に、n = 1 のときは a1 = a, b1 = b は互いに素なので、n = 2k ( k は整数 ) ならば an, bn は互いに素です。よって、ある値 N > n の任意の N で互いに素でなくなるという仮定に矛盾することになり、an, bn は常に互いに素でなければなりません。
最後に、n = 1 のとき a は奇数、an が奇数のとき an+1 = a・an + 2b・bn で、右辺の第一項は a, an が奇数なので奇数、第二項は偶数で、その和は奇数なので、an+1 は奇数です。従って、帰納法により任意の n に対して an は奇数となり、これで全て証明できました。
阪神・淡路大震災のときは早朝に家で、東日本大震災のときは会社で電話中に揺れを感じました。どちらも後でテレビを通じて被害の大きさに気づいたんですよね。原発の事故の様子を見た時は本当に恐ろしかったです。原発の廃炉への道のりは、まだまだかなり長く険しいようです。こんな状況でも原発を推進しようとするというのはやはり考えられないです。
NHK東日本大震災アーカイブス ( http://www9.nhk.or.jp/311shogen/ )
久々に、数学の問題に挑戦。京大の入試問題です。「誘導略」なので全然違う解き方をしているのかもしれません。また、合っている保証もないです。
-----
■ a, b を互いに素な自然数とする。a は奇数とする。自然数 n に対して 整数an, bn を ( a + b√2 )n = an + bn√2 を満たすように定めるとき、an と bn は互いに素であることを示せ( 2009 年京大理系乙誘導略 )
( an + bn√2 )( a + b√2 ) = ( a・an + 2b・bn ) + ( b・an + a・bn )√2 より
an+1 = a・an + 2b・bn
bn+1 = b・an + a・bn
が成り立ちます。an, bn が共通の因数 c を持つならば、an+1, bn+1 も同じ共通の因数 c を持つことになるので、ある値 n で an, bn が互いに素でなくなったら、N > n の任意の N でも an, bn は互いに素ではなくなります。
ところが、an, bn が互いに素であるとき、
( an + bn√2 )2 = ( an2 + 2bn2 ) + 2anbn√2 より
a2n = an2 + 2bn2
b2n = 2anbn
なので、an が奇数ならば an2 と 2bn2 には公約数はなく、a2n は 2, an, bn それぞれの素因数を約数として持ちません。逆に、2anbn は 2, an, bn それぞれの素因数の積しか約数にならないので、a_2n, b_2n は互いに素です。特に、n = 1 のときは a1 = a, b1 = b は互いに素なので、n = 2k ( k は整数 ) ならば an, bn は互いに素です。よって、ある値 N > n の任意の N で互いに素でなくなるという仮定に矛盾することになり、an, bn は常に互いに素でなければなりません。
最後に、n = 1 のとき a は奇数、an が奇数のとき an+1 = a・an + 2b・bn で、右辺の第一項は a, an が奇数なので奇数、第二項は偶数で、その和は奇数なので、an+1 は奇数です。従って、帰納法により任意の n に対して an は奇数となり、これで全て証明できました。
2015年02月07日
Nice to meet you
先週は海外のメーカーと会議 + 焼肉パーティーでした。
相変わらず英会話は苦手で、最近は海外メーカーとのやり取りも少なくなったので、以前よりも下手になっていました。やはり、普段から使っていないとダメなようです。洋楽や洋画で英語を聴くようにはしてるんですけどねえ。
今回も、「数学問題bot」に挑戦してみました。今まで何回か挑戦してきましたが、あえて解答は探して見たりしないようにしています。解答見て直してしまったら公開する意味はないですし、間違っているとわかってしまったら公開する気もなくなってしまうので、不正解の可能性があってもとりあえず出してしまっています。で、今回の問題は本当に自信がありません。なんだかあっけなさ過ぎて、どこかで勘違いしている可能性が大です。
-----
■ 実数に対して定義され実数を値にとる関数 f であって、任意の実数 x, y に対して f([x]y) = f(x)[f(y)] が成立するようなものを全て求めよ。ただし、[z] で z を超えない最大の整数を表すものとする(10国際数オリカザフスタン大会)
x = 0 を代入すると f(0) = f(0)[f(y)] となるので、これが任意の y で成り立つためには f(0) = 0 または [f(y)] = 1 である必要があります。
f(0) = 0 のとき、0 ≤ x < 1 に対して (左辺) = f(0) = 0、(右辺) = f(x)[f(y)] であり、0 = f(x)[f(y)] が任意の x, y で成り立つので、任意の x に対して f(x) = 0、または任意の y に対して [f(y)] = 0 です。前者は後者に含まれるので、[f(y)] = 0 が任意の y について成り立つ必要があります。
1 ≤ x < 2 に対して (左辺) = f(y)、(右辺) = f(x)[f(y)] であり、[f(y)] = 0 が任意の y について成り立つことから (右辺) = 0 です。従って f(y) = 0 が任意の y について成り立つことになり、f = 0 (定数) となります。
[f(y)] = 1 のとき、(右辺) = f(x)[f(y)] = f(x) が必ず成り立ちます。0 ≤ x < 1 に対しては (左辺) = f(0) なので、0 ≤ x < 1 では f(x) は定数 f(0) でなければなりません。
1 ≤ x < 2 のとき、(左辺) = f(y) より f(x) = f(y) が任意の x, y で成り立ちます。従って、f(x) は定数でなければなりません。[f(y)] = 1 より、1 ≤ f(y) < 2 なので、f = K ( 1 ≤ K < 2 ) となります。
従って、f = 0 または K ( K は 1 ≤ K < 2 を満たす定数 ) となります。
また、そのうち誤りに気がついて直すかもしれません。
相変わらず英会話は苦手で、最近は海外メーカーとのやり取りも少なくなったので、以前よりも下手になっていました。やはり、普段から使っていないとダメなようです。洋楽や洋画で英語を聴くようにはしてるんですけどねえ。
今回も、「数学問題bot」に挑戦してみました。今まで何回か挑戦してきましたが、あえて解答は探して見たりしないようにしています。解答見て直してしまったら公開する意味はないですし、間違っているとわかってしまったら公開する気もなくなってしまうので、不正解の可能性があってもとりあえず出してしまっています。で、今回の問題は本当に自信がありません。なんだかあっけなさ過ぎて、どこかで勘違いしている可能性が大です。
-----
■ 実数に対して定義され実数を値にとる関数 f であって、任意の実数 x, y に対して f([x]y) = f(x)[f(y)] が成立するようなものを全て求めよ。ただし、[z] で z を超えない最大の整数を表すものとする(10国際数オリカザフスタン大会)
x = 0 を代入すると f(0) = f(0)[f(y)] となるので、これが任意の y で成り立つためには f(0) = 0 または [f(y)] = 1 である必要があります。
f(0) = 0 のとき、0 ≤ x < 1 に対して (左辺) = f(0) = 0、(右辺) = f(x)[f(y)] であり、0 = f(x)[f(y)] が任意の x, y で成り立つので、任意の x に対して f(x) = 0、または任意の y に対して [f(y)] = 0 です。前者は後者に含まれるので、[f(y)] = 0 が任意の y について成り立つ必要があります。
1 ≤ x < 2 に対して (左辺) = f(y)、(右辺) = f(x)[f(y)] であり、[f(y)] = 0 が任意の y について成り立つことから (右辺) = 0 です。従って f(y) = 0 が任意の y について成り立つことになり、f = 0 (定数) となります。
[f(y)] = 1 のとき、(右辺) = f(x)[f(y)] = f(x) が必ず成り立ちます。0 ≤ x < 1 に対しては (左辺) = f(0) なので、0 ≤ x < 1 では f(x) は定数 f(0) でなければなりません。
1 ≤ x < 2 のとき、(左辺) = f(y) より f(x) = f(y) が任意の x, y で成り立ちます。従って、f(x) は定数でなければなりません。[f(y)] = 1 より、1 ≤ f(y) < 2 なので、f = K ( 1 ≤ K < 2 ) となります。
従って、f = 0 または K ( K は 1 ≤ K < 2 を満たす定数 ) となります。
また、そのうち誤りに気がついて直すかもしれません。
2015年01月28日
円と四角形
また急に寒くなってきました。
一月が終わる前に、「アルゴリズムのコーナー」にある「ハフマン符号化」をアップデートしたいと思っています。サンプル・プログラムは大体できたので、あとはドキュメントを見直すのみとなりました。何とか間に合わせて、二月からはアップデート作業と並行して「生存時間解析」あたりをまとめようかと考えてます。クラスタリングの手法が結構おもしろそうなので、これも作っていきたいのですが、そんなに時間が取れるかどうか...
中学校の頃に習った幾何の問題で、面白そうなのを見つけたので紹介します。Twitter から拾ってきたのですが、どこから見つけてきたのか失念してしまいました。
■ 円に内接する平行四辺形で長方形でないものは存在しないことを示せ。( 7mex 様 )
平行四辺形の向かい合う頂点の内角が等しいことと、円に内接する四角形の向かい合う頂点の内角和が 180 度であることを利用すると、円に内接する平行四辺形の内角は 90 度であることになるので必ず長方形になります。この二つの定理を証明する方がちょっとだけ大変です。
平行四辺形の向かい合う頂点の内角が等しいことは、相対する辺が平行なので、対角線を一本引いた時に錯角が等しくなることを利用すれば証明できます。
円に内接する四角形の向かい合う頂点の内角和が 180 度であることは次のように証明します。円の中心を各頂点と結んだ時に内部にできる 4 つの三角形が全て二等辺三角形であることから、それぞれの底角を○、□、△、×で表すと、向かい合う頂点の内角和が (二つの頂点をどのようにとっても) ○ + □ + △ + ×となるので、全頂点の内角和が 2( ○ + □ + △ + × ) = 360 度であることから ○ + □ + △ + × = 180 度となります。
中学校の頃にこれらの定理を習った記憶がありますが、どうやって証明するのか少し悩みました。
一月が終わる前に、「アルゴリズムのコーナー」にある「ハフマン符号化」をアップデートしたいと思っています。サンプル・プログラムは大体できたので、あとはドキュメントを見直すのみとなりました。何とか間に合わせて、二月からはアップデート作業と並行して「生存時間解析」あたりをまとめようかと考えてます。クラスタリングの手法が結構おもしろそうなので、これも作っていきたいのですが、そんなに時間が取れるかどうか...
中学校の頃に習った幾何の問題で、面白そうなのを見つけたので紹介します。Twitter から拾ってきたのですが、どこから見つけてきたのか失念してしまいました。
■ 円に内接する平行四辺形で長方形でないものは存在しないことを示せ。( 7mex 様 )
平行四辺形の向かい合う頂点の内角が等しいことと、円に内接する四角形の向かい合う頂点の内角和が 180 度であることを利用すると、円に内接する平行四辺形の内角は 90 度であることになるので必ず長方形になります。この二つの定理を証明する方がちょっとだけ大変です。
平行四辺形の向かい合う頂点の内角が等しいことは、相対する辺が平行なので、対角線を一本引いた時に錯角が等しくなることを利用すれば証明できます。
円に内接する四角形の向かい合う頂点の内角和が 180 度であることは次のように証明します。円の中心を各頂点と結んだ時に内部にできる 4 つの三角形が全て二等辺三角形であることから、それぞれの底角を○、□、△、×で表すと、向かい合う頂点の内角和が (二つの頂点をどのようにとっても) ○ + □ + △ + ×となるので、全頂点の内角和が 2( ○ + □ + △ + × ) = 360 度であることから ○ + □ + △ + × = 180 度となります。
中学校の頃にこれらの定理を習った記憶がありますが、どうやって証明するのか少し悩みました。
2015年01月19日
明日は大寒
明日は大寒。寒さに加えて風が強い日が続きますね。
昨日までセンター試験が行われたわけですが、なぜこんな一番寒い季節に試験なんかさせるんでしょうかね。体調を崩しやすい時期でもあるし、雪で交通機関がマヒしてしまったら最悪です。
今日の新聞のコラムを見ていたら一ヶ月ほど前倒しすればそんな問題も回避できるのではというようなことが書かれていました。クリスマスや正月前に試験が終われば多少は息抜きできそうですしね。
何はともあれ、受験生の皆さんはいよいよ二次試験を残すのみですね。現在、最後の追い込みといったところでしょうか。
ということで、「数学問題bot」にあった東工大の入試問題です。
-----
■ n を自然数、P(x) を n 次多項式とする。P(0), P(1), …, P(n) が整数ならば、全ての整数 k に対して P(k) は整数であることを証明せよ。( 08東工大AO )
* 以下にある Πj{1→n}( aj ) は a1 から an までの積を表します。
n = 1 ならば P(x) = ax + b に対し P(0) = b が整数、P(1) = a + b が整数なので a, b のどちらも整数であり、任意の整数 k に対して P(k) は整数であることが成り立ちます。
n 次以下の全ての多項式に対して成り立つと仮定して、( n + 1 ) 次の多項式を
P(x) = ax( x - 1 )( x - 2 ) ... ( x - n ) + R(x)
という形で表します。但し、a はゼロ以外の任意の数で、R(x) は n 次以下の多項式です。P(x) が k ≤ n のときに条件をみたすとすれば、P(k) = R(k) かつ P(k) は整数なので、R(k) は整数です。よって、R(x) は ( n 次以下の多項式なので ) 仮定から任意の整数 k についても整数であることになります。k = n + 1 のとき、
P( n + 1 ) = a( n + 1 )・n・( n - 1 ) ... ・1 + R( n + 1 ) = a( n + 1 )! + R( n + 1 )
が整数ならば、a = N / Πj{1→n+1}( jσj ) の形でなければなりません。但し、N は任意の整数、σj は 0 または 1 のいずれかの数です。任意の整数 k に対して
ak( k - 1 )( k - 2 ) ... ( k - n )
= ak! / ( k - n - 1 )!
= a( n + 1 )!k! / ( n + 1 )!( k - n - 1 )!
= a( n + 1 )!・kCn+1
より a( n + 1 )! は整数、kCn+1 も整数なので、ak( k - 1 )( k - 2 ) ... ( k - n ) は整数です。従って、任意の整数 k に対して P(k) は整数になります。以上から、帰納法により n 次式に対して P(0) から P(n) までが整数なら、任意の整数 k に対して P(k) が整数になることが証明できました。
二次式の場合で考えると、
P(x) = ax( x - 1 ) + ( bx + c )
に対して
P(0) = c
P(1) = b + c
がどちらも整数なので、b, c は整数であり、任意の整数 k に対して bk + c は整数です。
P(2) = 2a + 2b + c
も整数であり、2b + c が整数であることから 2a も整数になります。従って、a は分母として 2 しか持たず、任意の整数 N に対して N / 2 で表されます。任意の整数 k に対し、
ak( k - 1 ) = Nk( k - 1 ) / 2
は k と k - 1 のどちらかが必ず偶数となるので整数です。従って、任意の整数 k に対して P(k) は整数になります。
結構前に見つけた問題ですが、しばらく放置してました。ちょっと解いてみるかとチャレンジを始めてから実は一週間くらい経っています。また、例によって合っている保証はありません。
昨日までセンター試験が行われたわけですが、なぜこんな一番寒い季節に試験なんかさせるんでしょうかね。体調を崩しやすい時期でもあるし、雪で交通機関がマヒしてしまったら最悪です。
今日の新聞のコラムを見ていたら一ヶ月ほど前倒しすればそんな問題も回避できるのではというようなことが書かれていました。クリスマスや正月前に試験が終われば多少は息抜きできそうですしね。
何はともあれ、受験生の皆さんはいよいよ二次試験を残すのみですね。現在、最後の追い込みといったところでしょうか。
ということで、「数学問題bot」にあった東工大の入試問題です。
-----
■ n を自然数、P(x) を n 次多項式とする。P(0), P(1), …, P(n) が整数ならば、全ての整数 k に対して P(k) は整数であることを証明せよ。( 08東工大AO )
* 以下にある Πj{1→n}( aj ) は a1 から an までの積を表します。
n = 1 ならば P(x) = ax + b に対し P(0) = b が整数、P(1) = a + b が整数なので a, b のどちらも整数であり、任意の整数 k に対して P(k) は整数であることが成り立ちます。
n 次以下の全ての多項式に対して成り立つと仮定して、( n + 1 ) 次の多項式を
P(x) = ax( x - 1 )( x - 2 ) ... ( x - n ) + R(x)
という形で表します。但し、a はゼロ以外の任意の数で、R(x) は n 次以下の多項式です。P(x) が k ≤ n のときに条件をみたすとすれば、P(k) = R(k) かつ P(k) は整数なので、R(k) は整数です。よって、R(x) は ( n 次以下の多項式なので ) 仮定から任意の整数 k についても整数であることになります。k = n + 1 のとき、
P( n + 1 ) = a( n + 1 )・n・( n - 1 ) ... ・1 + R( n + 1 ) = a( n + 1 )! + R( n + 1 )
が整数ならば、a = N / Πj{1→n+1}( jσj ) の形でなければなりません。但し、N は任意の整数、σj は 0 または 1 のいずれかの数です。任意の整数 k に対して
ak( k - 1 )( k - 2 ) ... ( k - n )
= ak! / ( k - n - 1 )!
= a( n + 1 )!k! / ( n + 1 )!( k - n - 1 )!
= a( n + 1 )!・kCn+1
より a( n + 1 )! は整数、kCn+1 も整数なので、ak( k - 1 )( k - 2 ) ... ( k - n ) は整数です。従って、任意の整数 k に対して P(k) は整数になります。以上から、帰納法により n 次式に対して P(0) から P(n) までが整数なら、任意の整数 k に対して P(k) が整数になることが証明できました。
二次式の場合で考えると、
P(x) = ax( x - 1 ) + ( bx + c )
に対して
P(0) = c
P(1) = b + c
がどちらも整数なので、b, c は整数であり、任意の整数 k に対して bk + c は整数です。
P(2) = 2a + 2b + c
も整数であり、2b + c が整数であることから 2a も整数になります。従って、a は分母として 2 しか持たず、任意の整数 N に対して N / 2 で表されます。任意の整数 k に対し、
ak( k - 1 ) = Nk( k - 1 ) / 2
は k と k - 1 のどちらかが必ず偶数となるので整数です。従って、任意の整数 k に対して P(k) は整数になります。
結構前に見つけた問題ですが、しばらく放置してました。ちょっと解いてみるかとチャレンジを始めてから実は一週間くらい経っています。また、例によって合っている保証はありません。





