Fussy's Diary

今日は 3 月 11 日です。

Yahoo で「3.11」と検索すると、10 円が寄付されます。但し、3 月 11 日中だけです。今なら間に合いますよ。

2017 年名大入試問題の 3 問目です。そういえば、合格発表がすでにあったようですね。

-----

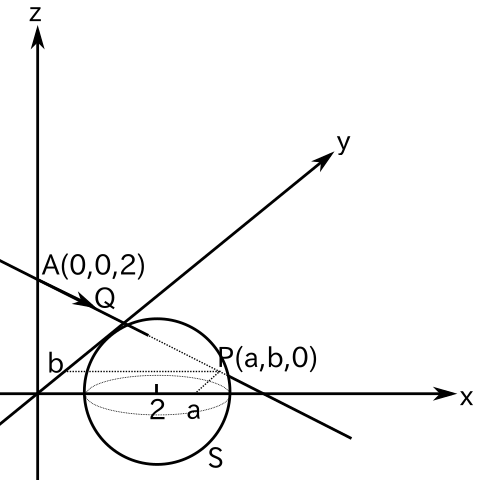
xyz 空間の 2 点 A( 0, 0, 2 ), P( a, b, 0 ) を通る直線を l とする。また、点 ( 2, 0, 0 ) を中心都市、半径が √2 である球面を S で表し、S のうち z 座標が z > 0 を満たす部分を T とする。このとき、次の問に答えよ。
(1) l 上に点 Q がある。実数 t を [AQ] = t[AP] ( [XY]は二点 X, Y を結ぶベクトルを表す ) で定めるとき、点 Q の座標を a, b, t を使って表せ。
(2) l が S と相異なる 2 点で交わるような実数 a, b に関する条件を求め、ab 平面上に図示せよ。
(3) l が T と相異なる 2 点で交わるような実数 a, b に関する条件を求め、ab 平面上に図示せよ。

(1) 図より Q( at, bt, 2 - 2t ) です。



(2) l と S の交点を Q とすると、( at - 2 )² + ( bt )² + ( 2 - 2t )² = 2 が成り立ちます。これを変形すると

( a² + b² + 4 )t² - ( 4a + 8 )t + 6 = 0

これが異なる実数解を持つためには判別式 D > 0 である必要があります。従って

D = ( 4a + 8 )² - 24( a² + b² + 4 )
= -8a² + 64a - 24b² - 32 > 0 より

a² - 8a + 3b² + 4 < 0
( a - 4 )² + 3b² < 12 が条件となります。



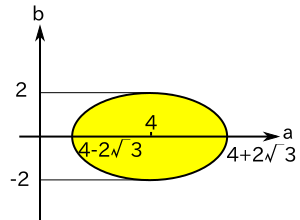
(3) P が球の内部にある場合、l は T 上の 1 点と、S の z ≤ 0 の領域の 1 点で交差することになります。従ってこの範囲では成り立たず、( a - 2 )² + b² > 2 でなければなりません。
P が球の外部にある場合、S の z > 0 の領域の 2 点で交差する場合が成り立つ範囲となります。f(t) = ( a² + b² + 4 )t² - ( 4a + 8 )t + 6 としたとき、|AQ| < |AP| となることからこの関数は t < 1 の領域で実数解を持つので



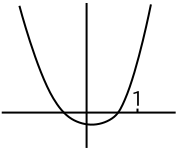
(i) f(1) > 0
(ii) f'(1) > 0

の二つが成り立つことになります。(i) より

f(1) = ( a² + b² + 4 ) - ( 4a + 8 ) + 6 = ( a - 2 )² + b² - 2 > 0

なのでこれは先程求めた範囲に等しくなります。また、(ii) より

f'(1) = 2( a² + b² + 4 ) - ( 4a + 8 ) = 2( a - 1 )² + 2b² - 2 > 0

なので、( a - 1 )² + b² > 1 がもう一つの範囲となります。(2) の結果と合わせると、求める条件は

( a - 4 )² + 3b² < 12
( a - 2 )² + b² > 2
( a - 1 )² + b² > 1

となります。

( a - 4 )² + 3b² = 12 と ( a - 2 )² + b² = 2 の交点は ( a, b ) = ( 1, ±1 ) です。
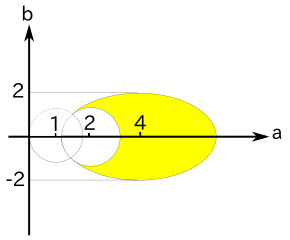
また、( a - 2 )² + b² = 2 と ( a - 1 )² + b² = 1 の交点も ( a, b ) = ( 1, ±1 ) で、この 3 つの曲線は同じ点 ( a, b ) = ( 1, ±1 ) で交わります。それに注意して図示すると以下のようになります。