2016年10月23日
不等式の問題
「アルゴリズムのコーナー」の「画像処理」の章を全てリニューアルしました。主にサンプル・プログラムの見直しを行っています。
「シーム・カービング」は試してみて非常に楽しいアルゴリズムなので、時間があれば他にもいろいろと試してみたいです。また、そのうちに更新を行うかもしれませんが、当分は先の話になりそうです。まだ作ってみたいものは他にもたくさんありますし。
「数学問題bot」から不等式の問題です。最初は手も足も出ない状態でしたが、ふと思い立った方法でなんとか証明してみました。例によって合っている保証はありません。
-----
不等式 (1/2)・(3/4)・(5/6)・ ... ・(999999/1000000) < 1/1000 を示せ ( 第 14 回シュプリンガー数学コンテスト )
命題の証明の前に、二つの補題を証明しておきます。
(補題 1) ( 1 - 1 / n )-n は単調減少で lim{n→∞} ( 1 - 1 / n )-n = e
f(x) = ln ( 1 - 1 / x )-x ( x > 1 ) とすると、
f(x) = -x ln ( 1 - 1 / x ) = -x ln ( x - 1 ) + x ln x
f'(x) = -ln ( x - 1 ) - x / ( x - 1 ) + ln x + 1 = -ln ( x - 1 ) + ln x - 1 / ( x - 1 )
f''(x) = -1 / ( x - 1 ) + 1 / x + 1 / ( x - 1 )2
= [ -x( x - 1 ) + ( x - 1 )2 + x ] / x( x - 1 )2
= ( -x2 + x + x2 - 2x + 1 + x ) / x( x - 1 )2
= 1 / x( x - 1 )2 > 0
よって、f'(x) は単調増加です。また、
f'(x) = -ln ( x - 1 ) + ln x - 1 / ( x - 1 )
= ln ( 1 + 1 / ( x - 1 ) ) - 1 / ( x - 1 )
→ 0 ( x → ∞ )
なので f'(x) < 0 となり、f(x) は単調減少となることから ( 1 - 1 / n )-n も単調減少となります。
ネイピア数の定義より lim{n→∞} ( 1 + 1 / n )n = e であることを利用すると、
( 1 + 1 / n )n / ( 1 - 1 / n )-n
= ( 1 - 1 / n2 )n
= 1 - n( 1 / n2 ) + (1/2)n( n - 1 )( 1 / n2 )2 - ... + (-1)knCk( 1 / n2 )k + ... → 1 ( n → ∞ )
より lim{n→∞} ( 1 - 1 / n )-n = e となります。
(補題 2) 関数 ln x に対し、下図において A > B が常に成り立つ
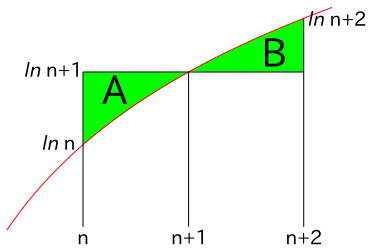
A = ln ( n + 1 ) - ∫{n→n+1} ln x dx
B = ∫{n+1→n+2} ln x dx - ln ( n + 1 )
より
A - B
= ln ( n + 1 ) - ∫{n→n+1} ln x dx - ∫{n+1→n+2} ln x dx + ln ( n + 1 )
= 2ln ( n + 1 ) - ∫{n→n+2} ln x dx
= 2ln ( n + 1 ) - [ x ln x ]{n→n+2} + [ x ]{n→n+2}
= 2ln ( n + 1 ) - ( n + 2 ) ln ( n + 2 ) + n ln n + 2
= ln ( n + 1 )2nne2 / ( n + 2 )n+2
= ln [ n / ( n + 2 ) ]n[ ( n + 1 ) / ( n + 2 ) ]2e2
となります。ここで
[ n / ( n + 2 ) ]n
= { [ 1 - 2 / ( n + 2 ) ](n+2)/2 }2[ ( n + 2 ) / n ]2
より
A - B = ln { [ 1 - 2 / ( n + 2 ) ](n+2)/2 }2[ ( n + 1 ) / n ]2e2
となり、補題 1 から { [ 1 - 2 / ( n + 2 ) ]-(n+2)/2 }2 は単調減少で → e2 ( n→∞ ) だから、{ [ 1 - 2 / ( n + 2 ) ](n+2)/2 }2 は単調増加で → 1 / e2 ( n→∞ ) となります。また、[ ( n + 1 ) / n ]2 → 1 ( n→∞ ) なので、A - B → ln ( 1 / e2 )・1・e2 = 0 ( n→∞ ) が成り立ちます。
n = 1 のとき、
A - B = ln ( 1 / 3 )( 2 / 3 )2e2 = ln ( 4 / 27 )e2 > ln ( 4 / 27 )( 2.7 )2 = ln 1.08 & gt; 0
なので、A - B が n の増加に対して単調減少であれば常に正であることになります。そこで、
f(x) = 2ln ( x + 1 ) - ( x + 2 ) ln ( x + 2 ) + x ln x + 2 ( x ≥ 1 )
とすると、
f'(x)
= 2 / ( x + 1 ) - ln ( x + 2 ) - 1 + ln x + 1
= 2 / ( x + 1 ) - ln ( x + 2 ) + ln x
f''(x)
= -2 / ( x + 1 )2 - 1 / ( x + 2 ) + 1 / x
= [ -2x( x + 2 ) - x( x + 1 )2 + ( x + 1 )2( x + 2 ) ] / x( x + 1 )2( x + 2 )
= [ -2x2 - 4x + 2( x + 1 )2 ] / x( x + 1 )2( x + 2 )
= 2 / x( x + 1 )2( x + 2 ) > 0
なので f'(x) は単調増加で、x = 1 のとき f'(1) = 1 - ln 3 > 0、f'(x) = 2 / ( x + 1 ) + ln ( 1 - 2 / ( x + 2 ) ) → 0 ( x→∞ ) だから、f'(x) < 0 が成り立ちます。よって f(x) は単調減少で、f(x) > 0 が常に成り立つことが証明されました。
(証明)
ln (1/2)・(3/4)・(5/6)・ ... ・(999999/1000000) = ( ln 1 + ln 3 + ... + ln 999999 ) - ( ln 2 + ln 4 + ... + ln 1000000 )
と変形できるので、左辺の二つの項についてその大きさを調べてみます。
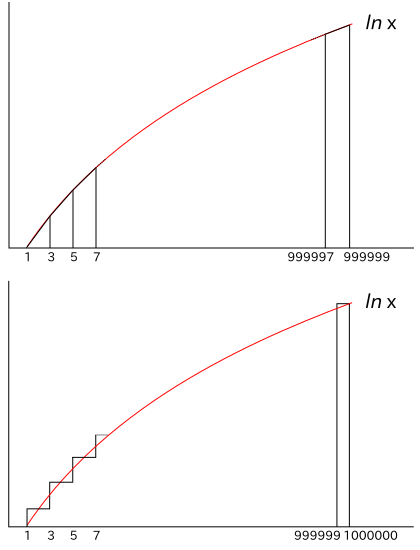
上図の上側の ln x と台形との面積の大きさを比較すると、
2( ln 1 + ln 3 ) / 2 + 2( ln 3 + ln 5 ) / 2 + ... 2( ln 999997 + ln 999999 ) / 2 < ∫{1→999999} ln x dx
が成り立ちます。この式は
ln1 + 2( ln 3 + ln 5 + ... + ln 999997 ) + ln 999999 < ∫{1→999999} ln x dx
と変形できて、ln 1 = 0 だから
ln1 + ln 3 + ln 5 + ... + ln 999997 + ln 999999 < (1/2)( ∫{1→999999} ln x dx + ln 999999 )
が成り立ちます。また、図の下側と補題 2 から
2 ln 2 + 2 ln 4 + 2 ln 6 + ... + ln 1000000 > ∫{1→1000000} ln x dx
なので、
ln 2 + ln 4 + ln 6 + ... + ln 1000000 > (1/2)( ∫{1→1000000} ln x dx + ln 1000000 )
となります。よって、
( ln 1 + ln 3 + ... + ln 999999 ) - ( ln 2 + ln 4 + ... + ln 1000000 ) < (1/2)( ∫{1→999999} ln x dx + ln 999999 - ∫{1→1000000} ln x dx + ln 1000000 )
ここで 1000000 = M, 999999 = m として右辺を変形すると
(右辺) = (1/2)[ ln ( m / M ) - ∫{m→M} ln x dx ]
∫{m→M} ln x dx
= [ x ln x ]{m→M} - &int{m→M} dx
= ln ( MM / mm ) - ( M - m )
= ln ( MM / mm ) - 1
よって
(右辺)
= (1/2)[ ln ( m / M ) - ln ( MM / mm ) + 1 )
= (1/2) ln ( mmme / MMM )
= (1/2) ln ( ( m / M )M( e / M ) )
= (1/2) ln ( ( 1 - 1 / M )M( e / M ) )
となります。補題 1 から
( 1 - 1 / M )M = 1 / ( 1 - 1 / M )-M → 1 / e ( M→∞ )
であり、( 1 - 1 / M )-M は単調減少だから ( 1 - 1 / M )-M > e より ( 1 - 1 / M )M < 1 / e となって、
( ln 1 + ln 3 + ... + ln 999999 ) - ( ln 2 + ln 4 + ... + ln 1000000 )
< (1/2)( ∫{1→999999} ln x dx + ln 999999 - ∫{1→1000000} ln x dx + ln 1000000 )
< (1/2)ln 1 / 1000000 = ln ( 1 / 1000 )
よって、不等式が証明されました。
「シーム・カービング」は試してみて非常に楽しいアルゴリズムなので、時間があれば他にもいろいろと試してみたいです。また、そのうちに更新を行うかもしれませんが、当分は先の話になりそうです。まだ作ってみたいものは他にもたくさんありますし。
「数学問題bot」から不等式の問題です。最初は手も足も出ない状態でしたが、ふと思い立った方法でなんとか証明してみました。例によって合っている保証はありません。
-----
不等式 (1/2)・(3/4)・(5/6)・ ... ・(999999/1000000) < 1/1000 を示せ ( 第 14 回シュプリンガー数学コンテスト )
命題の証明の前に、二つの補題を証明しておきます。
(補題 1) ( 1 - 1 / n )-n は単調減少で lim{n→∞} ( 1 - 1 / n )-n = e
f(x) = ln ( 1 - 1 / x )-x ( x > 1 ) とすると、
f(x) = -x ln ( 1 - 1 / x ) = -x ln ( x - 1 ) + x ln x
f'(x) = -ln ( x - 1 ) - x / ( x - 1 ) + ln x + 1 = -ln ( x - 1 ) + ln x - 1 / ( x - 1 )
f''(x) = -1 / ( x - 1 ) + 1 / x + 1 / ( x - 1 )2
= [ -x( x - 1 ) + ( x - 1 )2 + x ] / x( x - 1 )2
= ( -x2 + x + x2 - 2x + 1 + x ) / x( x - 1 )2
= 1 / x( x - 1 )2 > 0
よって、f'(x) は単調増加です。また、
f'(x) = -ln ( x - 1 ) + ln x - 1 / ( x - 1 )
= ln ( 1 + 1 / ( x - 1 ) ) - 1 / ( x - 1 )
→ 0 ( x → ∞ )
なので f'(x) < 0 となり、f(x) は単調減少となることから ( 1 - 1 / n )-n も単調減少となります。
ネイピア数の定義より lim{n→∞} ( 1 + 1 / n )n = e であることを利用すると、
( 1 + 1 / n )n / ( 1 - 1 / n )-n
= ( 1 - 1 / n2 )n
= 1 - n( 1 / n2 ) + (1/2)n( n - 1 )( 1 / n2 )2 - ... + (-1)knCk( 1 / n2 )k + ... → 1 ( n → ∞ )
より lim{n→∞} ( 1 - 1 / n )-n = e となります。
(補題 2) 関数 ln x に対し、下図において A > B が常に成り立つ

A = ln ( n + 1 ) - ∫{n→n+1} ln x dx
B = ∫{n+1→n+2} ln x dx - ln ( n + 1 )
より
A - B
= ln ( n + 1 ) - ∫{n→n+1} ln x dx - ∫{n+1→n+2} ln x dx + ln ( n + 1 )
= 2ln ( n + 1 ) - ∫{n→n+2} ln x dx
= 2ln ( n + 1 ) - [ x ln x ]{n→n+2} + [ x ]{n→n+2}
= 2ln ( n + 1 ) - ( n + 2 ) ln ( n + 2 ) + n ln n + 2
= ln ( n + 1 )2nne2 / ( n + 2 )n+2
= ln [ n / ( n + 2 ) ]n[ ( n + 1 ) / ( n + 2 ) ]2e2
となります。ここで
[ n / ( n + 2 ) ]n
= { [ 1 - 2 / ( n + 2 ) ](n+2)/2 }2[ ( n + 2 ) / n ]2
より
A - B = ln { [ 1 - 2 / ( n + 2 ) ](n+2)/2 }2[ ( n + 1 ) / n ]2e2
となり、補題 1 から { [ 1 - 2 / ( n + 2 ) ]-(n+2)/2 }2 は単調減少で → e2 ( n→∞ ) だから、{ [ 1 - 2 / ( n + 2 ) ](n+2)/2 }2 は単調増加で → 1 / e2 ( n→∞ ) となります。また、[ ( n + 1 ) / n ]2 → 1 ( n→∞ ) なので、A - B → ln ( 1 / e2 )・1・e2 = 0 ( n→∞ ) が成り立ちます。
n = 1 のとき、
A - B = ln ( 1 / 3 )( 2 / 3 )2e2 = ln ( 4 / 27 )e2 > ln ( 4 / 27 )( 2.7 )2 = ln 1.08 & gt; 0
なので、A - B が n の増加に対して単調減少であれば常に正であることになります。そこで、
f(x) = 2ln ( x + 1 ) - ( x + 2 ) ln ( x + 2 ) + x ln x + 2 ( x ≥ 1 )
とすると、
f'(x)
= 2 / ( x + 1 ) - ln ( x + 2 ) - 1 + ln x + 1
= 2 / ( x + 1 ) - ln ( x + 2 ) + ln x
f''(x)
= -2 / ( x + 1 )2 - 1 / ( x + 2 ) + 1 / x
= [ -2x( x + 2 ) - x( x + 1 )2 + ( x + 1 )2( x + 2 ) ] / x( x + 1 )2( x + 2 )
= [ -2x2 - 4x + 2( x + 1 )2 ] / x( x + 1 )2( x + 2 )
= 2 / x( x + 1 )2( x + 2 ) > 0
なので f'(x) は単調増加で、x = 1 のとき f'(1) = 1 - ln 3 > 0、f'(x) = 2 / ( x + 1 ) + ln ( 1 - 2 / ( x + 2 ) ) → 0 ( x→∞ ) だから、f'(x) < 0 が成り立ちます。よって f(x) は単調減少で、f(x) > 0 が常に成り立つことが証明されました。
(証明)
ln (1/2)・(3/4)・(5/6)・ ... ・(999999/1000000) = ( ln 1 + ln 3 + ... + ln 999999 ) - ( ln 2 + ln 4 + ... + ln 1000000 )
と変形できるので、左辺の二つの項についてその大きさを調べてみます。

上図の上側の ln x と台形との面積の大きさを比較すると、
2( ln 1 + ln 3 ) / 2 + 2( ln 3 + ln 5 ) / 2 + ... 2( ln 999997 + ln 999999 ) / 2 < ∫{1→999999} ln x dx
が成り立ちます。この式は
ln1 + 2( ln 3 + ln 5 + ... + ln 999997 ) + ln 999999 < ∫{1→999999} ln x dx
と変形できて、ln 1 = 0 だから
ln1 + ln 3 + ln 5 + ... + ln 999997 + ln 999999 < (1/2)( ∫{1→999999} ln x dx + ln 999999 )
が成り立ちます。また、図の下側と補題 2 から
2 ln 2 + 2 ln 4 + 2 ln 6 + ... + ln 1000000 > ∫{1→1000000} ln x dx
なので、
ln 2 + ln 4 + ln 6 + ... + ln 1000000 > (1/2)( ∫{1→1000000} ln x dx + ln 1000000 )
となります。よって、
( ln 1 + ln 3 + ... + ln 999999 ) - ( ln 2 + ln 4 + ... + ln 1000000 ) < (1/2)( ∫{1→999999} ln x dx + ln 999999 - ∫{1→1000000} ln x dx + ln 1000000 )
ここで 1000000 = M, 999999 = m として右辺を変形すると
(右辺) = (1/2)[ ln ( m / M ) - ∫{m→M} ln x dx ]
∫{m→M} ln x dx
= [ x ln x ]{m→M} - &int{m→M} dx
= ln ( MM / mm ) - ( M - m )
= ln ( MM / mm ) - 1
よって
(右辺)
= (1/2)[ ln ( m / M ) - ln ( MM / mm ) + 1 )
= (1/2) ln ( mmme / MMM )
= (1/2) ln ( ( m / M )M( e / M ) )
= (1/2) ln ( ( 1 - 1 / M )M( e / M ) )
となります。補題 1 から
( 1 - 1 / M )M = 1 / ( 1 - 1 / M )-M → 1 / e ( M→∞ )
であり、( 1 - 1 / M )-M は単調減少だから ( 1 - 1 / M )-M > e より ( 1 - 1 / M )M < 1 / e となって、
( ln 1 + ln 3 + ... + ln 999999 ) - ( ln 2 + ln 4 + ... + ln 1000000 )
< (1/2)( ∫{1→999999} ln x dx + ln 999999 - ∫{1→1000000} ln x dx + ln 1000000 )
< (1/2)ln 1 / 1000000 = ln ( 1 / 1000 )
よって、不等式が証明されました。





