2017年03月18日
名大入試問題 2017 (5)
歯医者で検診がありました。結果、虫歯が一本。治療が必要ということで憂うつです。
2017 年名大入試文系の問題です。去年と同様、全体的に文系のほうが難しいと感じました。
-----
a を正の定数とする。2 次関数 f(x) = ax2 と 3 次関数 g(x) x( x - 4 )2 について、次の問に答えよ。
(1) 関数 y = g(x) について、極値を求め、そのグラフを描け。
(2) 2 つの曲線 y = f(x) と y = g(x) は相異なる 3 点で交わることを示せ。
(3) 2 つの曲線 y = f(x) と y = g(x) で囲まれた 2 つの部分の面積が等しくなるように a の値を定めよ。またそのとき、2 つの曲線の交点の x 座標を求めよ。
(1) g(x) = x( x - 4 )2 より
g'(x) = ( x - 4 )2 + 2x( x - 4 )
= ( x - 4 )( 3x - 4 )
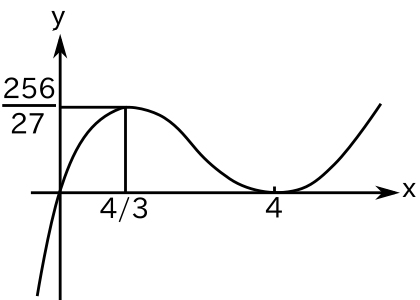
なので、x = 4, 4/3 のとき極値になります。g(4) = 0, g(4/3) = 256/27 で増減表は
なのでグラフは下図のようになります。
(2) f(x) = g(x) のとき、x( x - 4 )2 = ax2 より明らかに x = 0 を買いに持ちます。
x ≠ 0 のとき、両辺を x で割って ( x - 4 )2 = ax より
x2 - ( a + 8 )x + 16 = 0
の判別式 D を求めると
D = ( a + 8 )2 - 64 = a2 + 16a
となり、a は正の定数なので D > 0 より実数解は 2 つ存在します。従って、命題が成り立ちます。
(3) 2 つの解を r, s ( 但し r < s ) としたとき、
∫{0→s} x( x - 4 )2 - ax2 dx = 0
が成り立てばよいので、上式の左辺を計算すると
(左辺) = ∫{0→s} x3 - 8x2 + 16x - ax2 dx
= [ (1/4)x4 - (8/3)x3 + 8x2 - (a/3)x3 ]{0→s}
= (1/4)s4 - (8/3)s3 + 8s2 - (a/3)s3 = 0
となります。s ≠ 0 より左辺を s2 / 12 で割って
3s2 - ( 4a + 32 )s + 96 = 0
より a = (3/4)s + 24/s - 8 になります。r, s の値を計算すると
[ ( a + 8 ) ± ( a2 + 16a )1/2 ] / 2 で s は符号が + の方なので、
1/s = 2 / [ ( a + 8 ) ± ( a2 + 16a )1/2 ]
= [ ( a + 8 ) - ( a2 + 16a )1/2 ] / 32
より
a = (3/8)[ ( a + 8 ) + ( a2 + 16a )1/2 ] + (3/4)[ ( a + 8 ) - ( a2 + 16a )1/2 ] - 8
= (9/8)( a + 8 ) - (3/8)( a2 + 16a )1/2 - 8
となります。式を変形して
(1/8)a + 1 = (3/8)( a2 + 16a )1/2
より両辺に 8 を描けて 2 乗すると
( a + 8 )2 = 9( a2 + 16a )
式を整理して
a2 + 16a - 8 = 0
となります。従って
a = -8 ± 6√2
で a > 0 より a = -8 + 6√2 となります。このとき、r, s は
{ [ ( -8 + 6√2 ) + 8 ] ± [ ( -8 + 6√2 )2 + 16( -8 + 6√2 ) ]1/2 } / 2
= ( 6√2 ± √8 ) / 2 = 2√2, 4√2
と求められます。
2017 年名大入試文系の問題です。去年と同様、全体的に文系のほうが難しいと感じました。
-----
a を正の定数とする。2 次関数 f(x) = ax2 と 3 次関数 g(x) x( x - 4 )2 について、次の問に答えよ。
(1) 関数 y = g(x) について、極値を求め、そのグラフを描け。
(2) 2 つの曲線 y = f(x) と y = g(x) は相異なる 3 点で交わることを示せ。
(3) 2 つの曲線 y = f(x) と y = g(x) で囲まれた 2 つの部分の面積が等しくなるように a の値を定めよ。またそのとき、2 つの曲線の交点の x 座標を求めよ。
(1) g(x) = x( x - 4 )2 より
g'(x) = ( x - 4 )2 + 2x( x - 4 )
= ( x - 4 )( 3x - 4 )
なので、x = 4, 4/3 のとき極値になります。g(4) = 0, g(4/3) = 256/27 で増減表は
| x | 0 | 4/3 | 4 | ||||
|---|---|---|---|---|---|---|---|
| g(x) | - | 0 | + | 256/27 | + | 0 | - |
| g'(x) | + | 0 | - | 0 | + | ||
なのでグラフは下図のようになります。

(2) f(x) = g(x) のとき、x( x - 4 )2 = ax2 より明らかに x = 0 を買いに持ちます。
x ≠ 0 のとき、両辺を x で割って ( x - 4 )2 = ax より
x2 - ( a + 8 )x + 16 = 0
の判別式 D を求めると
D = ( a + 8 )2 - 64 = a2 + 16a
となり、a は正の定数なので D > 0 より実数解は 2 つ存在します。従って、命題が成り立ちます。
(3) 2 つの解を r, s ( 但し r < s ) としたとき、
∫{0→s} x( x - 4 )2 - ax2 dx = 0
が成り立てばよいので、上式の左辺を計算すると
(左辺) = ∫{0→s} x3 - 8x2 + 16x - ax2 dx
= [ (1/4)x4 - (8/3)x3 + 8x2 - (a/3)x3 ]{0→s}
= (1/4)s4 - (8/3)s3 + 8s2 - (a/3)s3 = 0
となります。s ≠ 0 より左辺を s2 / 12 で割って
3s2 - ( 4a + 32 )s + 96 = 0
より a = (3/4)s + 24/s - 8 になります。r, s の値を計算すると
[ ( a + 8 ) ± ( a2 + 16a )1/2 ] / 2 で s は符号が + の方なので、
1/s = 2 / [ ( a + 8 ) ± ( a2 + 16a )1/2 ]
= [ ( a + 8 ) - ( a2 + 16a )1/2 ] / 32
より
a = (3/8)[ ( a + 8 ) + ( a2 + 16a )1/2 ] + (3/4)[ ( a + 8 ) - ( a2 + 16a )1/2 ] - 8
= (9/8)( a + 8 ) - (3/8)( a2 + 16a )1/2 - 8
となります。式を変形して
(1/8)a + 1 = (3/8)( a2 + 16a )1/2
より両辺に 8 を描けて 2 乗すると
( a + 8 )2 = 9( a2 + 16a )
式を整理して
a2 + 16a - 8 = 0
となります。従って
a = -8 ± 6√2
で a > 0 より a = -8 + 6√2 となります。このとき、r, s は
{ [ ( -8 + 6√2 ) + 8 ] ± [ ( -8 + 6√2 )2 + 16( -8 + 6√2 ) ]1/2 } / 2
= ( 6√2 ± √8 ) / 2 = 2√2, 4√2
と求められます。





