2014年05月25日
ピタゴラスの定理
NHK の番組「ピタゴラスイッチ」は、古代ギリシャの数学者「ピタゴラス」が名前の由来になっていますが、番組の中の登場人物には「ピタ」「ゴラ」「スー」がいるということをついさっき知りました。
ピタゴラスの名前が付いた有名な定理「ピタゴラスの定理」は、直角三角形の斜辺の長さを c、その他の辺の長さを a, b としたときに
c2 = a2 + b2
が成り立つというもの。三平方の定理とも呼ばれ、確か小学校で習うのではなかったでしょうか。しかし、考え方を変えるとこの定理が
c = a + b
となってしまいます。
まず、最初に長方形からスタートして、四つの角のうちいずれかを長方形の形に 1 / 4 削ります。これで削った側には二つの角ができるので、次にこの角を長方形の形に 1 / 8 削ります。この操作を繰り返していきます。

操作を繰り返すと、その形は直角三角形にいくらでも近づきます。しかし、階段部分の長さはいくら削っても変化せず、斜辺以外の辺の和と等しいままです。この極限を考えると、斜辺の長さが他の二辺の和に等しい直角三角形ができあがります。斜辺に見える部分は実際には階段状態のままだから違うとも考えられますが、少なくとも面積はいくらでも近づけることができます。
少し前にこれを思い付き、矛盾点がどこかにないかを考えてみたのですが、今のところは解なしの状態です。フラクタル図形などと同じ考え方になるのでしょうかね。そもそも上のような図形は三角形とは呼べないですけどね。面積は限りなく等しい別の図形というとらえ方が正解なのかも。
ちなみに、ピタゴラスの定理の証明法はたくさんあります。その中の一つを紹介。
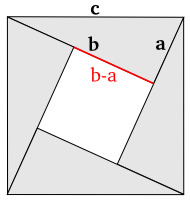
上図において、直角三角形の斜辺がちょうど大きな正方形の辺になるように配置されています。中央にできる小さな三角形は、直角三角形の二辺の差を一辺の長さとする正方形です。斜辺の長さを c、その他の辺の長さを a, b ( 但し b > a ) とすれば
大きな正方形の面積 = c2
四つの直角三角形の面積 = 4 x ab / 2 = 2ab
小さな正方形の面積 = ( b - a )2
なので、四つの直角三角形と小さな正方形の面積の和が大きな正方形の面積に等しくなることから
( b - a )2 + 2ab = a2 + b2 = c2
でピタゴラスの定理が得られます。他にも証明法はたくさんあるので、Wikipedia を参考に (但し、英語版の方です)。
ピタゴラスの名前が付いた有名な定理「ピタゴラスの定理」は、直角三角形の斜辺の長さを c、その他の辺の長さを a, b としたときに
c2 = a2 + b2
が成り立つというもの。三平方の定理とも呼ばれ、確か小学校で習うのではなかったでしょうか。しかし、考え方を変えるとこの定理が
c = a + b
となってしまいます。
まず、最初に長方形からスタートして、四つの角のうちいずれかを長方形の形に 1 / 4 削ります。これで削った側には二つの角ができるので、次にこの角を長方形の形に 1 / 8 削ります。この操作を繰り返していきます。

操作を繰り返すと、その形は直角三角形にいくらでも近づきます。しかし、階段部分の長さはいくら削っても変化せず、斜辺以外の辺の和と等しいままです。この極限を考えると、斜辺の長さが他の二辺の和に等しい直角三角形ができあがります。斜辺に見える部分は実際には階段状態のままだから違うとも考えられますが、少なくとも面積はいくらでも近づけることができます。
少し前にこれを思い付き、矛盾点がどこかにないかを考えてみたのですが、今のところは解なしの状態です。フラクタル図形などと同じ考え方になるのでしょうかね。そもそも上のような図形は三角形とは呼べないですけどね。面積は限りなく等しい別の図形というとらえ方が正解なのかも。
ちなみに、ピタゴラスの定理の証明法はたくさんあります。その中の一つを紹介。

上図において、直角三角形の斜辺がちょうど大きな正方形の辺になるように配置されています。中央にできる小さな三角形は、直角三角形の二辺の差を一辺の長さとする正方形です。斜辺の長さを c、その他の辺の長さを a, b ( 但し b > a ) とすれば
大きな正方形の面積 = c2
四つの直角三角形の面積 = 4 x ab / 2 = 2ab
小さな正方形の面積 = ( b - a )2
なので、四つの直角三角形と小さな正方形の面積の和が大きな正方形の面積に等しくなることから
( b - a )2 + 2ab = a2 + b2 = c2
でピタゴラスの定理が得られます。他にも証明法はたくさんあるので、Wikipedia を参考に (但し、英語版の方です)。
追記 2014/06/18
ふと思いついた結論は「いくら段の数を増やして元の三角形に近づけたとしても、段がある以上は三角形とはいえない」ということ。何だか当たり前のことですね。坂道に階段を設けたとして、段の数を増やせばいくらでも元の坂道に近づけられるというのも同じ意味になりますね。
ふと思いついた結論は「いくら段の数を増やして元の三角形に近づけたとしても、段がある以上は三角形とはいえない」ということ。何だか当たり前のことですね。坂道に階段を設けたとして、段の数を増やせばいくらでも元の坂道に近づけられるというのも同じ意味になりますね。
この記事へのトラックバックURL
http://fussy.mediacat-blog.jp/t99619





