Fussy's Diary

蒸し暑い夜です。温度計を見たら現在 27 度。

今日は一冊の本を紹介します。

「確率・統計入門」 小針あき宏著 (岩波書店)
ISBN 978-4-00-005157-6

著者はこの本が出版される前、原稿をひと通り書き上げて間もなく亡くなり、有志によって原稿の見直しを行なって出版されたという特異な経歴を持った参考書です。それなりの前提知識は必要で、自分も理解するのには非常に時間がかかりました。今では 7 〜 8 割程度は理解できたのではないかと思っていますが、それまでには他の参考書も利用する必要があったので、全てがこの一冊で足りるというわけにはいかないものの、逆にこの本のおかげでレベルをかなり上げることができたと思っています。書き方も独特で、ところどころにユーモアを交えつつ、突然高度な話題を持ちだしたりして一筋縄ではいかないところもあります。こんな癖のある参考書は他にはないでしょうね。

もし書店なんかで見かけたら最初の章に少し目を通してみて、もし面白そうだと感じることができれば購入することをお勧めします。最近になって、「確率空間」ではなく「確率モデル」という言葉を使った意味が本当に理解できるようになった気がします。  

NHK の番組「ピタゴラスイッチ」は、古代ギリシャの数学者「ピタゴラス」が名前の由来になっていますが、番組の中の登場人物には「ピタ」「ゴラ」「スー」がいるということをついさっき知りました。

ピタゴラスの名前が付いた有名な定理「ピタゴラスの定理」は、直角三角形の斜辺の長さを c、その他の辺の長さを a, b としたときに

c² = a² + b²

が成り立つというもの。三平方の定理とも呼ばれ、確か小学校で習うのではなかったでしょうか。しかし、考え方を変えるとこの定理が

c = a + b

となってしまいます。

まず、最初に長方形からスタートして、四つの角のうちいずれかを長方形の形に 1 / 4 削ります。これで削った側には二つの角ができるので、次にこの角を長方形の形に 1 / 8 削ります。この操作を繰り返していきます。



操作を繰り返すと、その形は直角三角形にいくらでも近づきます。しかし、階段部分の長さはいくら削っても変化せず、斜辺以外の辺の和と等しいままです。この極限を考えると、斜辺の長さが他の二辺の和に等しい直角三角形ができあがります。斜辺に見える部分は実際には階段状態のままだから違うとも考えられますが、少なくとも面積はいくらでも近づけることができます。

少し前にこれを思い付き、矛盾点がどこかにないかを考えてみたのですが、今のところは解なしの状態です。フラクタル図形などと同じ考え方になるのでしょうかね。そもそも上のような図形は三角形とは呼べないですけどね。面積は限りなく等しい別の図形というとらえ方が正解なのかも。

ちなみに、ピタゴラスの定理の証明法はたくさんあります。その中の一つを紹介。



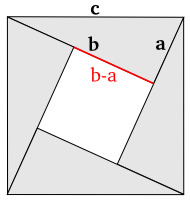
上図において、直角三角形の斜辺がちょうど大きな正方形の辺になるように配置されています。中央にできる小さな三角形は、直角三角形の二辺の差を一辺の長さとする正方形です。斜辺の長さを c、その他の辺の長さを a, b ( 但し b > a ) とすれば

大きな正方形の面積 = c²
四つの直角三角形の面積 = 4 x ab / 2 = 2ab
小さな正方形の面積 = ( b - a )²

なので、四つの直角三角形と小さな正方形の面積の和が大きな正方形の面積に等しくなることから

( b - a )² + 2ab = a² + b² = c²

でピタゴラスの定理が得られます。他にも証明法はたくさんあるので、Wikipedia を参考に (但し、英語版の方です)。  続きを読む

今日、テレビで喫茶「マウンテン」が紹介されてました。

他にはない奇抜なメニューで非常に有名な喫茶店ですが、20 年以上前からすでにその名は知られていて、近隣の学生(特に体育会系)に人気があったようです。小倉抹茶スパもその頃すでにあって、主に罰ゲームに利用されていたとか。食べた人からの話では小倉が口直しになるとのこと。麺のほうが小倉よりも甘いそうです。ちなみに、マウンテンで食事することを「山に登る」、完食出来たら「登頂」、途中で断念したら「遭難」といいます。それにしても、いつ頃から全国に知られるようになったんでしょうかね。自分はまだ食べたことはありません。
名古屋の名物として挙げられるものでいつも不思議に思うのが「エビフライ」と「みそカツ」で、少なくとも子供の頃は、「エビフライ」は名物などではなかったし「みそカツ」を食べた覚えもないです。これもいつ頃からそうなったのか、不思議です。

「数学問題 bot」で前から悩んでした問題がようやく解けました。解けないとなると意地になってしまい、昨日と今日はこの問題のことばかり考えていた気がします。

---

■ 自然数 n と m について、n² + m と n² - m がともに平方数であるなら、m は 24 で割り切れることを示せ (第24回シュプリンガー数学コンテスト)

n² + m = ( n + a )²
n² - m = ( n - b )²

とします。但し、b > 0, a > 0 とします。右辺を展開して整理すると、

n² + m = n² + 2na + a²
n² - m = n² - 2nb + b²

より

m = 2na + a²
m = 2nb - b²

なので、m について解くと

m = ab( a + b ) / ( b - a )

n について解くと

n = ( a² + b² ) / 2( b - a )
= [ ( b - a )² + 2ab ] / 2( b - a )
= ( b - a ) / 2 + ab / ( b - a )

となります。n の式から、a² + b² は偶数でなければ 2( b - a ) で割り切ることができないので、a, b はどちらも偶数または奇数となります。また、ab は b - a で割り切れる必要があり、a, b が両方とも奇数の場合、ab が奇数、b - a が偶数となるので、a, b はどちらも偶数である必要があります。そこで、a → 2a, b → 2b と置き換えて m, n を計算すると、

m = 2a・2b( 2a + 2b ) / ( 2b - 2a )
= 4ab( a + b ) / ( b - a )

n = ( 2b - 2a ) / 2 + 2a・2b / ( 2b - 2a )
= ( b - a ) + 2ab / ( b - a )

となります。n の式から、今度は 2ab が偶数であることから b - a も偶数である必要があるので b - a = 2c と置き換えると、

m = 4a( a + 2c )( 2a + 2c ) / 2c
= 4a( a + 2c )( a + c ) / c

n = 2c + 2a( a + 2c ) / 2c
= 2c + a( a + 2c ) / c

となります。n が整数となるためには、a/c, a/c + 2 のいずれかが整数となる必要があり、すなわち a が c で割り切れることになるので、a = kc として

m = 4kc( kc + 2c )( kc + c ) / c
= 4k( k + 1 )( k + 2 )c²

という結果が得られます。k, k + 1, k + 2 はいずれか一つが必ず 3 の倍数になり、少なくとも一つは偶数になるので、m は必ず 24 の倍数となります。

ところで、今までチャレンジした問題は数論が多いようです。特に選んでいるわけではないのですが、ほとんどパズルを解く感覚でやっているからでしょうか。今度は他のジャンルにも挑戦してみようと思います。  

最近、仕事が大変な状態でかなり疲れがたまっています。

「効率よく仕事しろ」 という言葉をよく聞きますが、個々人は効率よくこなしていこうとみんな努力してるんですよね。で、一番効率を悪くしているのが組織全体での決まりごと。とにかく誰が見ても明らかに効率が悪いのにそれが慣例化している。こういう企業は日本だけなんでしょうかね。

で、効率というキーワードでググってみたら、「仕事を効率良くこなすためのシンプルな 13 の習慣」というページを見つけました。古い記事ですが、役に立ちそうなことが列挙されています。すでに実践しているもの、何となくやっているものも含まれていますが、意識して仕事するようにするとまた違うかもしれませんね。もちろん、仕事だけではなくプライベートにも役に立ちそうです。

息抜きに「数学問題 bot」の問題を解いてみました。

---

■ 2 以上の自然数 n に対し、n と n² + 2 がともに素数になるのは n = 3 の場合に限ることを示せ。( 06 京都前期・理 )

n が 3 以外の素数の時、n² + 2 が合成数であることを証明すれば十分です。

n は 3 以外の素数なので、3 で割った時の余りは 1 か 2 のいずれかになります。従って、余りが 1 ならば n - 1 が、余りが 2 ならば n + 1 が 3 で割り切れます。従って、

n² + 2 = ( n + 1 )( n - 1 ) + 3

より n² + 2 は必ず 3 で割り切れることになり、n² + 2 は合成数です。

古典数論の問題は、実際に具体的な数値で試してみると解法が見つかることが多いです。この問題でも、n に素数を代入していくと

5² + 2 = 27
7² + 2 = 51
11² + 2 = 123

となって、全て 3 で割り切れることがわかります。

例によって、答えのチェックはしていないので合っているという保証はありません。  

明日で休日が終わり、またしばらくは忙しい毎日が始まります。

昨日・今日はのんびりと過ごしていました。ぼんやりと次のテーマも考えていて、そのための本を読んだりもしていましたが、いつの間にか睡魔におそわれて眠ってしまい大して進んでいません。まあ、今まで通りあせらずにゆっくりとやっていくつもりです。

夕方頃から、「数学問題 bot」にチャレンジしていました。二問のうち片方は解けたので、解法を紹介してみたいと思います。これもあっているという保証はないです。

---

■ 2ⁿ + n² が素数であるような 2 以上の整数 n について、n を 6 で割った時の余りが 3 であることを示せ(第24回シュプリンガー数学コンテスト)

このまま眺めていても取り付く島もない状態なので、とりあえず小さな数からチェックしてみます。

n = 3 のとき 2³ + 3² = 8 + 9 = 17 で素数。
n = 4 のとき 2⁴ + 4² = 16 + 16 = 32
n = 5 のとき 2⁵ + 5² = 32 + 25 = 57
n = 6 のとき 2⁶ + 6² = 64 + 36 = 100
n = 7 のとき 2⁷ + 7² = 128 + 49 = 177
n = 8 のとき 2⁸ + 8² = 256 + 64 = 320
n = 9 のとき 2⁹ + 9² = 512 + 81 = 593 で素数。

明らかに、n が偶数なら 2ⁿ + n² も偶数なので除外できます。n = 5, 7 のとき結果は 3 の倍数なので、n = 6k ± 1 ( k > 0 ) としたときにこれが 3 の倍数となるのではと推測してみます。そこで、この値を 2ⁿ + n² に代入して変形してみると、

2^6k±1 + ( 6k ± 1 )² = 36k² ± 12k + ( 2^6k±1 + 1 )

となります。もし任意の k に対して、2^6k±1 + 1 が 3 で割り切れれば、つまり 2^6k±1 を 3 で割った余りが 2 なら、2ⁿ + n² は 3 で割り切れることになって必ず合成数となります。k = 1 のとき、

2^6k-1 = 2⁵ = 32
2^6k+1 = 2⁷ = 128

なので、どちらも 3 で割ると 2 余ります。3m + 2 で表される ( 3 で割って 2 余る) 数に 2⁶ = 64 を掛けると

( 3m + 2 ) x 64 = 3 x 64m + 128 = 3 x ( 64m + 42 ) + 2 より やはり 2 余る数になるので、2^6k±1 は任意の k に対して必ず 2 余ることになり、n = 6k ± 1 の場合は必ず 3 の倍数なので素数にはならないことが示されました。よって、2ⁿ + n² が素数になるなら、それは必ず n = 6k + 3 で表されることになります。

逆は成り立つのでしょうか。

n = 15 のとき 2¹⁵ + 15² = 32768 + 225 = 32993 で素数。
n = 21 のとき 2²¹ + 21² = 2097152 + 441 = 2097593 で素数。
n = 27 のとき 2²⁷ + 27² = 134217728 + 729 = 134218457 で素数ではない(73 x 521 x 3529 )。

となるので、必ず成り立つというわけではありません。

ところで、下の問題も同時に考えていました。こちらの方が簡単だと思っていたのに、まだ解けていません。解法が見つかったらまた紹介しようかと思います。

■ 自然数 n と m について、n² + m とn² - m がともに平方数であるなら、m は 24 で割り切れることを示せ (第24回シュプリンガー数学コンテスト)
  

連休もあとわずかとなりました。

Daily Portal Z で 「オオグソクムシはカニとかシャコに近い味」という記事を発見。あの巨大なダンゴムシの親分を食べるの ? と思ったら、それは「ダイオウグソクムシ」で、「オオグソクムシ」は日本で獲れるもっと小さな種でした (ちなみに「ダイオウグソクムシ」は鳥羽水族館で実際に見ることができます)。

とは言ってもダンゴムシの親分に変わりはなく (実際、ダンゴムシやフナムシの仲間だそうです)、まさか食べられるとは思いませんでした。確かにダンゴムシも食用になると聞いたことはありますけどね。で、味はカニによく似ているとのことですが、残念ながら身の部分は非常に少なくたくさんは食べられなかったようです。

オオグソクムシ、写真を見るとなかなかかわいい顔をしています。しかし、裏返すとゴ○ブリに形が似ているというのが残念。ダイオウグソクムシの人気が結構高い気がするので、これを機会にオオグソクムシにももっと注目してほしいところ。

久々に「数学問題 bot」に挑戦。本当は他の問題にもチャレンジしていたのですが、解けたのはこれだけ (例によって答え合わせをしていないので合っている保証はありません)。

---

■ 1 から 5 までの自然数を 1 列に並べる。どの並べ方も同様の確からしさで発生する。このとき 1 番目と 2 番目と 3 番目の数の和と、3 番目と 4 番目と 5 番目の数の和が等しくなる確率を求めよ。ただし、各並べ方において、それぞれの数字は重複なく１度ずつ用いるものとする (10京都・理甲)

「1 番目と 2 番目と 3 番目の数の和と、3 番目と 4 番目と 5 番目の数の和が等しくなる」ということは、「1 番目と 2 番目の数の和と、4 番目と 5 番目の数の和が等しくなる」ことと同じなので、3 番目の数は無視できます。また、1 から 5 までの自然数の和は 15 で、1, 2, 4, 5 番目の数の和は 15 から 3 番目の数を引いた値になります。その結果は偶数でないと半分に分けることができないので、3 番目の数は必ず奇数の 1, 3, 5 となります。

ここから、i 番目の数を a[i] で表します。仮に、a[3] = 1 ならば、a[1] + a[2] = a[4] + a[5] = 7 になります。2 から 5 までの数でこの条件を満たす組み合わせは ( 2, 5 ) と ( 3, 4 ) のペアだけです。それぞれは ( a[1], a[2] ) と ( a[4], a[5] ) の間で交換が可能で、さらにその内部でも交換が可能なので、並べ方は 2 x 2 x 2 = 8 通りになります。a[1] から a[5] までを実際に並べてみると

( 2 5 1 3 4 ) ( 5 2 1 3 4 ) ( 2 5 1 4 3 ) ( 5 2 1 4 3 )
( 3 4 1 2 5 ) ( 4 3 1 2 5 ) ( 3 4 1 5 2 ) ( 4 3 1 5 2 )

です。a[3] = 3 ならば、組み合わせは ( 1, 5 ) と ( 2, 4 ) のペア、a[3] = 5 ならば、組み合わせは ( 1, 4 ) と ( 2, 3 ) のペアのみなので、やはりそれぞれ 8 通りです。よって、条件を満たす組み合わせは 8 x 3 = 24 通りとなります。最後に、全ての並べ方は 5! = 120 通りなので、確率は

24 / 120 = 1 / 5

となります。  

Twitter でおもしろいツイートを見つけました。

Zeno’s Paradox: Understanding Convergent & Divergent Series http://t.co/9DnkuNG2HP

— LiveScience (@LiveScience) 2014, 5月 1

「ゼノンのパラドックス」は「アキレスとカメ」の話が特に有名です。前方にいるカメをアキレスが追いかけるとします。その間の距離が 100m 離れていて、アキレスの方がカメよりも 10 倍速ければ、最初にカメのいた地点にアキレスが到達した時カメは 10m 先にいます。さらに追いかけてその地点に到達した時、カメは 1m 先にいます。これを繰り返していくと、10cm、1cm、1mm と距離は 1 / 10 ずつ短くなるものの、いつまで経っても間の距離はゼロになりません。つまり、永遠に追い越すことができないというのが、ギリシャ時代のの哲学者ゼノンの主張したパラドックスです。初めてこれを知ったのは確か小学生の頃で、当時は不思議に感じた記憶があります。

数学的には、有限な数を無限に続く和の形で表すことができることを意味します。例えば、

1 = 1 / 2 + 1 / 4 + 1 / 8 + 1 / 16 + ... + 1 / 2ⁿ + ...

というような式が挙げられます。ようかんなんかを半分に切る操作を無限に繰り返す様子をイメージすれば納得できるかと思います。
似たような話として、例えば 1 を 3 で割ると、

1 / 3 = 0.333333 ...

と 3 が無限に続きます。これに 3 を掛けると

0.333333 ... x 3 = 0.999999 ...

です。しかし、これは 1 / 3 x 3 を計算していることでもあるので答えは 1 にもなります。従って、

0.999999 ... = 1

という結論になります。このあたりを考えだすと頭が痛くなってくるので、この辺でやめておきます。  

今日も寒い一日でした。本当に四月中旬なんだろうか。

明日はいつもより 30 分ほど早く起きなければいけません。少々ヘコんでいます。ちなみにいつもは 6 時に起きてます。寝るのがだいたい 0 時頃になるので 6 時間は寝ていることになります。しかし、睡眠時間が足りないようで、昼食後は眠気に襲われて特につらいです。
適正な睡眠時間は人によってバラバラで、通常は 6 時間程度と言われていますが自分の場合はもう少し必要なようです。睡眠時間は 1.5 時間単位にするとよいという事もあって、6 時間で足りなければ 7.5 時間眠ればいいものの、そこまで増やすことはできそうにありません。なので、休みの日にゆっくり眠ることで補うようにはしてます。そうは言ってもなかなか難しいですけどね。

今日も「アルゴリズムのコーナー」の作成をしていました。しかし、同じ事ばかり考えていると頭が煮つまってくるので、途中で「数学問題 bot」から問題を選んで悩んでました。

---

任意に選ばれた 4 つの整数を一度ずつ使い、四則演算子によって数式を作る。この時必ず 10 の倍数が作れることを示せ(wand125様)

まず、10 の倍数になるためには一桁目がゼロになればよく、一桁目の数は各整数の一桁目だけで決まるので、二桁目以降は無視できます。よって、ここからは一桁目の数だけを考えます。ゼロが入ればその数を掛けることでゼロになるので除外できます。また、同じ数が含まれればその差はゼロになるのでやはり除外できます。すると、考えられる組み合わせは 1 から 9 までの数から 4 つを選択する場合に限定されます。その数は

₉C₄ = 126 通り

です。まだひとつずつチェックするには大変な数なのでもう少し絞り込みます。

5 と偶数の両方が含まれるとそれらを掛けあわせることでゼロにすることができます。また、( 1, 9 )( 2, 8 )( 3, 7 )( 4, 6 ) の組み合わせも和はゼロになります。5 と奇数だけの組み合わせにすると、1, 3, 7, 9 の中から三つ選ぶ必要があり、どの組み合わせをとっても和がゼロになるペアが含まれるので、5 を含む場合は必ず 10 の倍数にすることができます。1, 2, 3, 4, 6, 7, 8, 9 から 4 つ選択し、かつ和がゼロになるペアを含まないようにするためには、( 1, 2, 3, 4 ) と ( 9, 8, 7, 6 ) の二つの組み合わせに対し、同じ位置の数を反転させて作られる全ての組み合わせだけを考えなければなりません。それは 2⁴ = 16 通りあります。それらを列挙して調べてみると、

1, 2, 3, 4 ... 3 - 2 - 1 = 0
1, 2, 3, 6 ... 3 - 2 - 1 = 0
1, 2, 7, 4 ... 7 + 2 + 1 = 10
1, 8, 3, 4 ... 4 - 3 - 1 = 0
9, 2, 3, 4 ... 9 - 4 - 3 - 2 = 0
1, 2, 7, 6 ... 7 + 2 + 1 = 10
1, 8, 3, 6 ... 6 + 3 + 1 = 10
9, 2, 3, 6 ... 9 - 6 - 3 = 0
1, 8, 7, 4 ... 8 - 7 - 1 = 0
9, 2, 7, 4 ... 9 - 7 - 2 = 0
9, 8, 3, 4 ... 9 + 4 - 3 = 10
1, 8, 7, 6 ... 1 + 6 - 7 = 0
9, 2, 7, 6 ... 9 - 7 - 2 = 0
9, 8, 3, 6 ... 9 - 6 - 3 = 0
9, 8, 7, 4 ... 9 + 8 - 7 = 10
9, 8, 7, 6 ... 9 + 8 - 7 = 10

従って、必ず 10 の倍数が作れることになります。

---

他の問題を考えると、煮詰まっていた頭が整理できたりするようですね。最後に、この問題を考案して下さった wand125 様に感謝します。

それにしても、今月中に更新できるのか不安になってきました。あと三つほどヤマを越さなければいけません...  

暑くなったり、寒くなったり。調子が悪くなりそうです。

金曜日に飲み会があり、今日はしんどい一日でした。いや、二日酔いになるほど飲んではないんですけど、終了後すぐに電車に飛び乗って、座ることもできなかったので体の方は相当まいっていた模様。それでも、飲み会のおかげで作成できなかった週報を帰宅後に家で書いていました。しかし、途中で休憩を入れたら眠ってしまい、気がついたら朝の 8 時過ぎ。とりあえず週報を作成するためそのまま起きることに。昼食・夕食後に仮眠をとったので、だいぶマシな状態にはなりました。

さて、「数学問題 bot」から 2003 年の名古屋大の問題を選択してみました。

---

n を自然数とするとき m ≤ n で m と n の最大公約数が 1 となる自然数の個数を f(n) とする。
(中略)
2) p, q を互いに異なる素数とする。このとき f(pq) を求めよ。

pq 以下の自然数で、pq と互いに素ではない (最大公約数が 1 でない) 数は、0 < n < p の範囲の自然数 n と q の積 nq と 0 < m < q の範囲の自然数 m と p の積 mp、最後に pq そのものの 3 種類あります。
nq の個数は q から ( p - 1 )q までの p - 1 個。
mp の個数は p から ( q - 1 )p までの q - 1 個。

よって、pq 以下の自然数で pq と互いに素でない数は ( p - 1 ) + ( q - 1 ) + 1 = p + q - 1 個あり、1 から pq までは pq 個の数があるので、pq 以下の自然数で pq と互いに素となる数の個数 f(pq) は

f(pq) = pq - ( p + q - 1 ) = ( p - 1 )( q - 1 )個

になります。

---

さらに、素数 p のべき乗に対して、f( p^k ) を求めてみましょう。

p^k 以下の自然数で p^k と互いに素でない数は、0 < n ≤ p^k-1 の範囲の自然数 n と p の積 np となる数なので、その数は p^k-1 個です。したがって、p^k 以下の自然数で p^k と互いに素となる数の個数 f( p^k ) は

f( p^k ) = p^k - p^k-1

になります。実は、任意の自然数 m と n が互いに素であれば、

f(mn) = f(m)f(n)

が成り立ちます。また、この関数 f の正体は「オイラーのφ関数 φ(m)」で、数学者オイラー ( Leonhard Euler ) が最初に紹介したと言われています。

a と m が互いに素であれば、a の φ(m) 乗を m で割った時の余りは必ず 1 になります。これを

a^φ(m) ≡ 1 ( mod m )

と表します。m が素数 p のとき φ(p) = p - 1 なので、上式は

a^p-1 ≡ 1 ( mod p )

です。これは「フェルマーの小定理」という有名な定理です。

もし、詳細を知りたいという方は「はじめての数論」という書籍を紹介しておきます。大学入試にも出題される可能性があるので、受験生の方も読んでおいて損はないと思います。

はじめての数論 原著第3版 -- 発見と証明の大航海-ピタゴラスの定理から楕円曲線まで  

今日の「NHK白熱教室」は行動経済学という聞きなれない分野がテーマでした。

人は周囲に同調しやすいもの。それがいい方向に働く場合もあれば、イラク戦争での虐待のように悪い結果になることもあるという話でした。結構面白いしタメになる話も多く、時間があれば来週も見てみようかなと思います。
四種類のビールを注文させた時、アメリカでは人とは違うものを注文しがちなのに対して、香港では同じものを注文する傾向があるそうです。どちらも周囲の影響を受けているのは変わらず、それに対してどう思うのかが異なるということですね。そしてその結果、どちらも満足度は下がってしまうそうです。自分が本当に注文したかったものを選べなかったわけなので。さて、何か注文する場合に自分はどうかなと考えてみましたが、どうやら他の人よりも周囲の影響を受けにくいようです。いわゆる「空気がよめない」人間なわけですね。しかし、ネットで何か購入するときは他の人の批評に左右されやすいですね。こういうのは「優柔不断」といいます。

さて、「数学問題 bot」から今回は 2010 年の名古屋大の問題です。

---

xy 平面上で x, y 座標共に整数である点を格子点と呼ぶ。(中略) a, b は実数で a ≠ 0 とする。y=ax² + bx のグラフ上に点 ( 0, 0 ) 以外に格子点が 2 つ存在すれば、無限個存在することを示せ。

y = F(x) とします。格子点の x 座標を m, n ( 但し m ≠ 0, n ≠ 0, m ≠ n ) とすると、F(m) = am² + bm と F(n) = an² + bn は整数です。このとき、

nF(m) - mF(n) = n( am² + bm ) - m( an² + bn ) = amn( m - n )
n²F(m) - m²F(n) = n²( am² + bm ) - m²( an² + bn ) = bmn( n - m )

より amn( m - n ) と bmn( n - m ) も整数で、

F( mn( m - n ) ) = a[ mn( m - n ) ]² + bmn( m - n )
= amn( m - n )・mn( m - n ) - bmn( n - m )
= [ nF(m) - mF(n) ]・mn( m - n ) - [ n²F(m) - m²F(n) ]

となるので F( mn( m - n ) ) も整数です。よって、mn( m - n ) ≠ m or n の場合、m と n から新たな格子点の x 座標 mn( m - n ) を求める操作を繰り返すことで格子点を無限に生成することができます。

mn( m - n ) = m になる場合は n = ±1, m - n = ±1 より

( m, n ) = ( 2, 1 ), ( -2, -1 )

であり、これらの点を通るならば 4a ± 2b と a ± b は整数になります。したがって、

( 4a ± 2b ) - 2( a ± b ) = 2a
( 4a ± 2b ) - 4( a ± b ) = -2b

より 2a, 2b も整数で、m が偶数 2p ならば

F( 2p ) = a(2p)² + b(2p) = 2a(2p²) + (2b)p

は整数なので、x が偶数の場合は格子点になり、これは無限個存在します。

---

例によって正解はこれだけはないかもしれないし、正解しているという保証もありません。二つの格子点の座標で係数 a, b を表すとどうなるかを考えているうちに上のような証明になりました。  

今日も不安定な天気でした。

本日は大阪で石川智晶さんのライブが行われていました。次は六月に東京であるのですが、昨日から発売開始ですでに完売、キャンセル待ちという状態です。完全に油断していました。今度は名古屋や大阪であるのかどうかわかりませんからね。とりあえずキャンセルを待つことにします。

話は変わって、今回は数学者オイラーが導き出した「オイラーの公式」を紹介します。この式は

e^iθ = cosθ + isinθ

というもの。i は虚数で -1 の平方根、e はネイピア数です。この式を覚えておくと、三角関数の様々な公式を導くことができます。例えば、

e^i(α+β)
= cos(α+β) + isin(α+β)

e^i(α+β)
= e^iαe^iβ
= ( cosα + isinα )( cosβ + isinβ )
= ( cosαcosβ - sinαsinβ )
+ i( sinαcosβ + cosαsinβ )

なので、加法定理のうちの

sin(α+β ) = sinαcosβ + cosαsinβ
cos(α+β ) = cosαcosβ - sinαsinβ

が得られます。これは高校の頃、暗記するのが大変な上に、導出も幾何的に解こうとすると結構面倒だったので苦手でした。この頃に教えてもらっていたら、もっと楽できたような気がします。便利な式なので、受験生の方にはぜひとも覚えておいてほしいと思います。

ちなみに小野洋子さんの小説「博士の愛した数式」で登場する式は、オイラーの公式に θ = π を代入することで得られます。

e^iπ = cosπ + isinπ = -1

「博士の愛した数式」は自分も読みましたが、非常にいい小説でしたよ。  

四月というのに、また急に寒くなりました。

先週から桜が満開です。朝の出勤時に川沿いの桜並木を通るので、いい目の保養になります。夜になると控えめにライトアップされた夜桜を見ることもできるので、遠出しなくても桜を楽しめるというのはいい環境に住んでいるなと感じます。
「アルゴリズムのコーナー」の次の内容がだいたい固まってきて、現在作成中です。しかし、まだ時間は掛かりそうです。今年に入ってからの更新頻度はあまりよくない状況が続いています。今は内容を理解しながら作成することが多いので、どうしても時間が掛かってしまいます。それでも気力の続く限りは継続しますけどね。

で、また現実逃避で「数学問題 bot」から一部だけ解いてみました。正解しているという保証は相変わらずありません。

■ 0 でない自然数の最右端の数字を、最左端に移動する操作を考える。

(i) この操作によってもとの数の 2 倍になる最小の自然数を求めよ
(ii) k = 3, ... , 9 に対して、この操作で k 倍になる最小の自然数を求めよ。

とりあえず (i) だけ解いています。おそらくもっと簡単な解法があると思いますが、もし見つかったらまた公開します。

(解法)

元の数を 10M + N とします。N が最右端の数で、M は残りの数です。N を最左端に移動すると、元の数の桁数が K ならばその数は 10^K x N + M になります。これが元の数の 2 倍なので

2( 10M + N ) = 10^K x N + M より

( 10^K - 2 )N = 19M

が成り立ちます。但し、N は一桁の数であること、また M は K 桁 ( 10^K-1 のオーダー ) の数であることが制約事項となります。

N < 10 なので、N は 19 では割りきれません。したがって、10^K - 2 は 19 で割り切れる必要があり、10^K を 19 で割った余りは 2 となります。K を 1 から順に増やしていくと

1 : 10 / 19 = 0 ... 10
2 : 10² / 19 = 5 ... 5
3 : 5 x 10 / 19 = 2 ... 12
4 : 12 x 10 / 19 = 6 ... 6
5 : 6 x 10 / 19 = 3 ... 3
6 : 3 x 10 / 19 = 1 ... 11
7 : 11 x 10 / 19 = 5 ... 15
8 : 15 x 10 / 19 = 7 ... 17
9 : 17 x 10 / 19 = 8 ... 18
10 : 18 x 10 / 19 = 9 ... 9
11 : 9 x 10 / 19 = 4 ... 14
12 : 14 x 10 / 19 = 7 ... 7
13 : 7 x 10 / 19 = 3 ... 13
14 : 13 x 10 / 19 = 6 ... 16
15 : 16 x 10 / 19 = 8 ... 8
16 : 8 x 10 / 19 = 4 ... 4
17 : 4 x 10 / 19 = 2 ... 2

K = 17 のときに剰余が 2 になりました。但し、A x B の剰余が A の剰余と B との積から求められることを利用しています。

この結果から、10¹⁷ - 2 は 19 で割り切ることができて、その商はすでに上の結果から 5,263,157,894,736,842 となることがわかります (上の結果の商を順番に並べるだけです)。しかし、これは 10¹⁵ のオーダーなので、10¹⁶ のオーダーにするために N = 2 として M = 10,526,315,789,473,684 とします。

したがって、求める自然数は 105,263,157,894,736,842 となります。

この方法の場合、k = 4 のときは

( 10^K - 4 )N = 39M

なので、N が 3 の倍数のときは 10^K - 4 は 13 で割り切ることができればよいことになり少々面倒になります。求めた数を見ると、ある位の数の二倍の一桁目が次の位の数になるので、これを利用すればもっと簡単な解法が見つかるのかもしれません ( それより前に正解している保証もないです )。  

行き詰まった時についつい挑戦したくなります。おかげで本題の方がなかなか進みません。しばらくは封印したいと思います。

■ p を素数、n を正の整数とするとき、( pⁿ )! は p で何回割り切れるか (09京都・文理)

1 から pⁿ までの数の中に、p の倍数は p^n-1 個ある。なぜなら、p の倍数は p 個おきに見つかるから。同様に考えれば、p² の倍数は p^n-2 個ある。これを続けると、最終的には pⁿ の倍数として pⁿ そのものが 1 個だけ見つかる。

p² の倍数は p の倍数でもあるので、1 個分が p の倍数の個数分に含まれる。p² の倍数 1 個に対しては 2 個の p が含まれるので、残りは p^n-2 個になる。p³ の倍数は p² と p の倍数でもあり、すでに 2 個分はカウントされているので、残りは p^n-3 個。

従って、Σ{0→n-1}( p^k ) を求めれば 1 から pⁿ までの数の中に含まれる p の個数が得られる。これは、(pⁿ)! に含まれる p の個数そのものである。

パズルみたいで解いていて結構楽しかったです。小さな数で実際に試してみるのが理解する一番の近道でしょうか。  

もうすぐ 4 月です。会社の組織変更で人の入れ替えが多く、明日は送別会が予定されています。

「数学問題 bot」から、もう一問解いてみました。2009 年の東北大の問題です。

1) a + b = c のとき、a³ + b³ ＋ 3abc = c³ を示せ。
2) a + b ≥ ｃ のとき、a³ + b³ + 3abc ≥ c³ を示せ。

1) は簡単なので 2) だけ。

a³ + b³ + 3abc - c³
= ( a + b )³ - 3ab( a + b ) + 3abc - c³
= ( a + b - c )[ ( a + b )² + ( a + b )c + c² ] - 3ab( a + b - c )
= ( a + b - c )[ ( a + b )² + ( a + b )c + c² - 3ab ]
= ( a + b - c )( a² + b² + c² - ab + bc + ca )
= ( a + b - c )[ ( a - b )² + ( b + c )² + ( c + a )² ] / 2

a + b ≥ c より a + b - c ≥ 0 なので (上式) ≥ 0 になる。

式の変形に気付くことができれば簡単だと思いますが、時間のあるときに悩んで二日ほどでやっと解けたといったところです。
暇つぶしに適当な問題に挑戦するのは結構いい頭の体操になります。問題は、出題される数が多くて目移りしてしまうこと...  

Twitter で面白いアカウントを見つけました。「数学問題 bot」というアカウントです。問題を一つ選んで挑戦してみました。

「1 から 11 までの自然数からなる集合を N とする。N をどのように 2 つの集合 A, B に分割 ( N = A ∪ Bかつ A ∩ B ＝ ∅ )しても、A または B の部分集合 S で、S に属する要素の和がちょうど 12 になるものが存在することを示せ」

要は、1 から 11 までの数をどのように二つに分けても、どちらかに和が 12 となるような組み合わせが存在するという意味です。とりあえず解いてみましたが、後で回答を見つけて確認したところ、最初だけ一致していたものの途中から異なる証明をしていました。一応合っているとは思うのですが ...

(解法)

二つの要素の和が 12 になる組み合わせは ( 1, 11 ), ( 2, 10 ), ( 3, 9 ), ( 4, 8 ), ( 5, 7 ) の 5 つ。従って、これらのペアが同じ集合に属すれば必ず和が 12 になる要素が見つかる。各組み合わせの要素が全て異なる集合に属する場合を考えると、残りの要素 6 がどちらに入るのかを考慮すれば 2⁵ = 32 通りになる。全ての場合において和が 12 になる要素が存在すれば証明できる。6 を除けば、対称性から 16 通りを考えればよいので、まずは 16 通りを調べて和が 12 となる組み合わせがなければ 6 を追加することにする (結局 6 は不要となりました)。

なお、3 つ以上の要素から和が 12 になる組み合わせは

( 1, 2, 9 ) ( 1, 2, 3, 6 ) ( 1, 2, 4, 5 )
( 1, 3, 8 ) ( 1, 4, 7 ) ( 1, 5, 6 )
( 2, 3, 7 ) ( 2, 4, 6 )
( 3, 4, 5 )

がある。

以下、A = { 1, 2, 3, 4, 5 }, B = { 11, 10, 9, 8, 7 } を初期状態として、5 桁の二値データはペアの要素を入れ替えた個所を 1 で表しているものとする。例えば、00001 ならば 5 と 7 を入れ替えたもの。二値データが二つあるのは、どちらも A, B を入れ替えただけで同じ意味になるから (ちなみにビット反転すればもう片方のデータが得られます)。

1) 00000 11111
A 1 2 3 4 5 → [1 2 4 5]
B 11 10 9 8 7

2) 00001 11110
A 1 2 3 4 7 → [2 3 7]
B 11 10 9 8 5

3) 00010 11101
A 1 2 3 8 5 → [1 3 8]
B 11 10 9 4 7

4) 00011 11100
A 1 2 3 8 7 → [1 3 8]
B 11 10 9 4 5

5) 00100 11011
A 1 2 9 4 5 → [1 2 4 5]
B 11 10 3 8 7

6) 00101 11010
A 1 2 9 4 7 → [1 4 7]
B 11 10 3 8 5

7) 00110 11001
A 1 2 9 8 5 → [1 2 9]
B 11 10 3 4 7

8) 00111 11000
A 1 2 9 8 7 → [1 2 9]
B 11 10 3 4 5

9) 01000 10111
A 1 10 3 4 5 → [3 4 5]
B 11 2 9 8 7

10) 01001 10110
A 1 10 3 4 7 → [1 4 7]
B 11 2 9 8 5

11) 01010 10101
A 1 10 3 8 5 → [1 3 8]
B 11 2 9 4 7

12) 01011 10100
A 1 10 3 8 7 → [1 3 8]
B 11 2 9 4 5

13) 01100 10011
A 1 10 9 4 5
B 11 2 3 8 7 → [2 3 7]

14) 01101 10010
A 1 10 9 4 7 → [1 4 7]
B 11 2 3 8 5

15) 01110 10001
A 1 10 9 8 5
B 11 2 3 4 7 → [2 3 7]

16) 01111 10000
A 1 10 9 8 7
B 11 2 3 4 5 → [3 4 5]

これで、全ての場合に対して和が 12 となる要素があることが証明された。