2015年09月27日
十五夜を見ながら一問
今日は空も晴れて満月がきれいです。
写真に撮ってみましたが、あまりきれいには写らないですね。

やっぱり、天体望遠鏡がほしくなってくるこの頃です。
「数学問題bot」から、図形の問題にチャレンジです。
-----
3 以上の自然数 n に対して、一辺の長さが 1 の正方形に含まれる面積最大の正 n 角形の面積を Sn とする。S3 と S6 を求めよ。( 近畿大学第 9 回数学コンテスト )
正三角形の面積は一辺の長さによって大小関係が決まります。正方形の中にできるだけ長い辺を持った正三角形が収まるように配置すればいいわけですが、正三角形の少なくとも二つの頂点が正三角形の辺に接するように配置する方が大きくなるのは明らかです。そのような配置の仕方で一辺だけが正方形内に入るようにしたとき、その最小は正三角形の一辺が正方形の一辺に接する配置の仕方で、最大は正方形の対角線が正三角形の一辺になるような配置の仕方です。
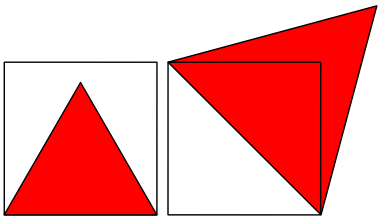
しかし、最小となる配置の場合はもう一つの頂点が正方形の内部にあり、まだ大きくする余地があります。逆に最大となる配置はもう一つの頂点が正方形の外側にあるので条件を満たしません。そこで、正方形と正三角形の頂点が重なっているところを一点だけ選んで固定し、もう一点は正方形の辺上を移動させます。最小となる配置の場合、正三角形はだんだん大きくなり、逆に最大の場合は小さくなっていきます。やがて、もう一つの頂点が正方形の辺上に位置することになります。
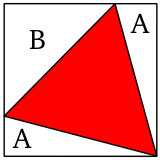
上図の二つの三角形 A は直角三角形で、斜辺は正三角形の辺、もう一辺が正方形の辺なので二つは合同です。従って三角形 B は直角二等辺三角形となります。三角形 A の一つの鋭角は 15 度なので、短い方の辺の長さは sin 15 度になります。これを x とすれば三角形 A の面積は x / 2、三角形 B の面積は ( 1 - x )2 / 2 です。よって、
S3
= 1 - ( x / 2 ) x 2 - ( 1 - x )2 / 2
= ( 1 - x )[ 1 - ( 1 - x ) / 2 ]
= ( 1 - x )( 1 + x ) / 2
= ( 1 - x2 ) / 2
となります。
cos 2θ = 1 - 2sin2θ
より
x2 = ( 1 - cos 30度 ) / 2 = ( 1 - √3 / 2 ) / 2
となって、
S3 = [ 1 - ( 1 - √3 / 2 ) / 2 ] / 2 = 1 / 4 + √3 / 8
となります。
S6 については、次の図を見ればわかりやすいかと思います。
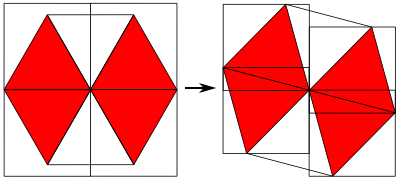
但し、小さい正方形の一辺は 1 / 2 なので、一つの三角形の面積は S3 の 1 / 4 となります。よって、
S6 = S3 x 6 / 4 = 3 / 8 + 3√3 / 16
となります。
例によって、合っているという保証なしです。
写真に撮ってみましたが、あまりきれいには写らないですね。

やっぱり、天体望遠鏡がほしくなってくるこの頃です。
「数学問題bot」から、図形の問題にチャレンジです。
-----
3 以上の自然数 n に対して、一辺の長さが 1 の正方形に含まれる面積最大の正 n 角形の面積を Sn とする。S3 と S6 を求めよ。( 近畿大学第 9 回数学コンテスト )
正三角形の面積は一辺の長さによって大小関係が決まります。正方形の中にできるだけ長い辺を持った正三角形が収まるように配置すればいいわけですが、正三角形の少なくとも二つの頂点が正三角形の辺に接するように配置する方が大きくなるのは明らかです。そのような配置の仕方で一辺だけが正方形内に入るようにしたとき、その最小は正三角形の一辺が正方形の一辺に接する配置の仕方で、最大は正方形の対角線が正三角形の一辺になるような配置の仕方です。

しかし、最小となる配置の場合はもう一つの頂点が正方形の内部にあり、まだ大きくする余地があります。逆に最大となる配置はもう一つの頂点が正方形の外側にあるので条件を満たしません。そこで、正方形と正三角形の頂点が重なっているところを一点だけ選んで固定し、もう一点は正方形の辺上を移動させます。最小となる配置の場合、正三角形はだんだん大きくなり、逆に最大の場合は小さくなっていきます。やがて、もう一つの頂点が正方形の辺上に位置することになります。

上図の二つの三角形 A は直角三角形で、斜辺は正三角形の辺、もう一辺が正方形の辺なので二つは合同です。従って三角形 B は直角二等辺三角形となります。三角形 A の一つの鋭角は 15 度なので、短い方の辺の長さは sin 15 度になります。これを x とすれば三角形 A の面積は x / 2、三角形 B の面積は ( 1 - x )2 / 2 です。よって、
S3
= 1 - ( x / 2 ) x 2 - ( 1 - x )2 / 2
= ( 1 - x )[ 1 - ( 1 - x ) / 2 ]
= ( 1 - x )( 1 + x ) / 2
= ( 1 - x2 ) / 2
となります。
cos 2θ = 1 - 2sin2θ
より
x2 = ( 1 - cos 30度 ) / 2 = ( 1 - √3 / 2 ) / 2
となって、
S3 = [ 1 - ( 1 - √3 / 2 ) / 2 ] / 2 = 1 / 4 + √3 / 8
となります。
S6 については、次の図を見ればわかりやすいかと思います。

但し、小さい正方形の一辺は 1 / 2 なので、一つの三角形の面積は S3 の 1 / 4 となります。よって、
S6 = S3 x 6 / 4 = 3 / 8 + 3√3 / 16
となります。
例によって、合っているという保証なしです。





